Giải bài tập SGK Toán 6 Bài 14: Tìm giá trị phân số của một số cho trước

Tìm:

a) \( \displaystyle {2 \over 3}\) của 8,7;            b) \( \displaystyle {2 \over 7}\) của \( \displaystyle {-11 \over 6}\);

c) \( \displaystyle 2{1 \over 3}\) của 5,1;          d) \( \displaystyle 2{7 \over {11}}\) của \( \displaystyle 6{3 \over 5}\). 

Hướng dẫn giải

Câu a:

\( \displaystyle {2 \over 3}\) của 8, 7 là: 

\( \displaystyle {2 \over 3}.8,7 = {2 \over 3}.{{87} \over {10}} = {{58} \over {10}} = 5,8\)

Câu b:

\( \displaystyle {2 \over 7}\) của \( \displaystyle {-11 \over 6}\) là:

\( \displaystyle {2 \over 7}.{{ - 11} \over 6}= {{ 2.(- 11)} \over {7.6}} = {{ - 11} \over {21}}\)

Câu c:

\( \displaystyle 2{1 \over 3}\) của 5,1 là: 

\( \displaystyle 2{1 \over 3}.5,1=2{1 \over 3}.{{51} \over {10}} = {7 \over 3}.{{51} \over {10}} = {{119} \over {10}} \)\(= 11,9\)

Câu d:

\( \displaystyle 2{7 \over {11}}\) của \( \displaystyle 6{3 \over 5}\) là:

\( \displaystyle 2{7 \over {11}}.6{3 \over 5} = {{29} \over {11}}.{{33} \over 5} = {{29.33} \over 11.5} = {{87} \over 5}\). 

Hãy so sánh 16% của 25 và 25% của 16. Dựa vào nhận xét đó hãy tính nhanh.

a) 84% của 25 ;              b) 48% của 50. 

Hướng dẫn giải

16% của 25 bằng \(\dfrac{16}{100}.25=\dfrac{16.25}{100} = 4\) ;

25% của 16 bằng \(\dfrac{25}{100}.16=\dfrac{25.16}{100} = 4\) .

Do đó 16% của 25 bằng 25% của 16.

Câu a:

Tương tự 84% của 25 bằng 25% của 84 mà 25% của 84 bằng \(25\% .84 = \dfrac{1}{4}.84 = 21\)

Vậy 84% của 25 bằng 21.

Câu b:

48% của 50 bằng 50% của 48, mà 50% của 48 bằng \(50\% .48 = \dfrac{1}{2}.48 = 24\)

Vậy 48% của 50 bằng 24. 

Biết rằng 13,21 . 3 = 39,63 và 39,63 : 5 = 7,926. Hãy tìm \(\dfrac{3}{5}\) của 13,21 và \(\dfrac{5}{3}\) của 7,926 mà không cần tính toán.

Hướng dẫn giải

Ta có: \(\dfrac{3}{5}\) của 13,21 bằng \(\dfrac{3}{5}.13,21\)

\(=\dfrac{3.13,21}{5}= (13,21 . 3) : 5\)  

\(=39,63:5\) (theo đề bài)

\(=7,926\) (theo đề bài)

Vậy theo đề bài \(\dfrac{3}{5}\) của 13,21 bằng 7,926.

Ta có: \(\dfrac{5}{3}\) của 7,926 bằng 

\(\dfrac{5}{3}.7,926 = \dfrac{5}{3}.\dfrac{{39,63}}{5} \)\(= \dfrac{5}{3}.\dfrac{{13,21.3}}{5} = \dfrac{5}{3}.\dfrac{3}{5}.13,21 \)\(= 13,21\)

Vậy \(\dfrac{5}{3}\) của 7,926 bằng 13,21. 

Tuấn có 21 viên bi. Tuấn cho Dũng \(\dfrac{3}{7}\) số bi của mình. Hỏi

a) Dũng được Tuấn cho bao nhiêu viên bi?

b) Tuấn còn lại bao nhiêu viên bi?

Hướng dẫn giải

Câu a:

Dũng được Tuấn cho số viên bi là:

\(21.\dfrac{3}{7} = 9\) (viên bi)

Câu b:

Tuấn còn lại số viên bi là: \( 21 - 9 = 12\) (viên bi)

Đố : An nói :" Lấy một phần hai của một phần hai rồi đem chia cho một phần hai sẽ được kết quả là một phần hai". Đố em bạn An nói có đúng không? 

Hướng dẫn giải

Lấy \( \displaystyle {1 \over 2}\) của \( \displaystyle {1 \over 2}\) là lấy \( \displaystyle {1 \over 2}.{1 \over 2}\)

Lấy \( \displaystyle {1 \over 2}.{1 \over 2}\) chia cho \( \displaystyle {1 \over 2}\) ta có:

\( \displaystyle \left( {{1 \over 2}.{1 \over 2}} \right):{1 \over 2} = {1 \over 4}.{2 \over 1} = {1 \over 2}\)

Vậy An nói đúng. 

Sử dụng máy tính bỏ túi.

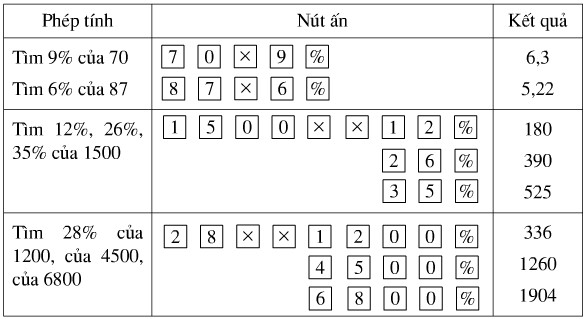
Sử dụng máy tính bỏ túi để tính :

a) 3,7% của 13,5;                  b) 6,5% của 52,61 ;

c) 17% . 29% của 2534;              d) 48% của 264, 395, 1836.

Các bạn bấm máy tính như phần hướng dẫn ở bảng trên.

Hướng dẫn giải

Câu a:

3.7% của 13,5 là: 0,4995 

Câu b:

6,5% của 52,61 là: 3,41965

Câu c:

17% của 2534 là: 430,78

29% của 2534 là: 734,86

47% của 2534 là: 1190,98

Câu d:

48% của 264 là: 126,72

48% của 395 là: 189,6

48% của 1836 là: 881,28

Đoạn đường sắt Hà Nội – Hải Phòng dài 102 km. Một xe lửa xuất phát từ Hà Nội đã đi được \(\displaystyle {3 \over 5}\) quãng đường. Hỏi xe lửa còn cách Hải Phòng bao nhiêu Kilomet? 

Hướng dẫn giải

Xe lửa xuất phát từ Hà Nội đi được quãng đường là:

 \(\displaystyle 102.{3 \over 5} = 61,2(km)\)

Vậy xe lửa còn cách Hải Phòng:

\(102 – 61,2 = 40,8 (km)\) 

Vậy xe lửa còn cách Hải Phòng: 40,8 (km).

Nguyên liệu để muối dưa cải gồm rau cải, hành tươi, đường và muối. Khối lượng hành, đường muối theo thứ tự bằng 5%, \( \displaystyle {1 \over {1000}}\) và \( \displaystyle {3 \over {40}}\) khối lượng rau cải. Vậy nếu muối 2 kg rau cải thì cần bao nhiêu ki lô gam hành, đường và muối?  

Số kg hành cần để muối 2kg rau cải là:

 \( \displaystyle 2.5\%  = 2.\frac{5}{{100}} = 0,1\left( {kg} \right)\)

Số kg đường cần để muối 2kg rau cải là:

 \( \displaystyle 2 \times {1 \over {1000}} = 0,002(kg)\)

Số kg muối cần để muối 2kg rau cải là:

\( \displaystyle 2 \times {3 \over {40}} = 0,15\) (kg)

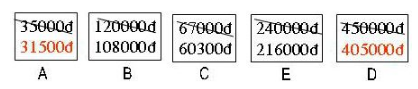
Nhân dịp lễ Quốc Khánh 2 – 9, một cửa hàng giảm giá 10% một số mặt hàng. Người bán hàng đã sửa lại giá của các mặt hàng ấy như sau:

Em hãy kiểm tra xem người bán hàng tính giá mới có đúng không?

Hướng dẫn giải

Ta có: Giảm 10% tức là bán  \(\displaystyle 90\% ={{90} \over {100}}\) giá ban đầu, ta đi tìm \(\displaystyle {{90} \over {100}}\) giá ban đầu (giá gốc) sẽ ra giá bán đã được giảm giá.

\( \displaystyle A.\,35000.{{90} \over {100}} = 31500\)đ ≠ 33000 đ    (Sai)

\( \displaystyle B.\,120000.{{90} \over {100}} = 108000\)đ      (Đúng)

\( \displaystyle C.\,67000.{{90} \over {100}} = 60300\)đ          (Đúng)

\( \displaystyle D.\,450000.{{90} \over {100}} = 405000\)đ ≠ 420000đ          (Sai)

\( \displaystyle E.\,240000.{{90} \over {100}} = 216000\)đ      (Đúng) 

Kết luận: Người bán hàng sửa giá đúng các mặt hàng B, C, E.

Sửa giá sai các mặt hàng A, D. 

Sử dụng máy tính bỏ túi

Ví dụ: Một quyển sách giá 8000đ. Tìm giá mới của quyển sách sau khi giảm giá 15%.

Vậy giá mới của quyển sách là 6800đ.

Theo cách trên, em hãy dùng máy tính bỏ túi để kiểm tra giá mới của các mặt hàng nêu ở bài tập 123.

Hướng dẫn giải

Ta bấm:

35000 x 15 % - 

120000 x 15 % - 

67000 x 15 % - 

240000 x 15 % - 

450000 x 15 % - 

Kết quả:

A, D (sai); B, C, E (đúng)

Bố bạn Lan gửi tiết kiệm 1 triệu đồng tại một ngân hàng theo thể thức “có kì hạn 12 tháng” với lãi suất 0,58% một tháng (tiền lãi một tháng bằng 0,58% số tiền gửi ban đầu và sau 12 tháng mới được lấy lãi). Hỏi hết thời hạn 12 tháng ấy, bố bạn lấy ra cả vốn lẫn lãi được bao nhiêu? 

Hướng dẫn giải

Tiền lãi trong một tháng là:

\(0,58 \%  . 1000000 \)\(\displaystyle ={{0,58} \over {100}}. 1000000 = 5800\) (đồng)

Tiền lãi của 12 tháng là: 

\(5800 . 12 = 69600\) (đồng) 

Tiền vốn lẫn lãi sau 12 tháng là:

\(1000000 + 69600 = 1069600\) (đồng)