Giải bài tập SGK Toán 6 Ôn tập chương 2: Số nguyên
Phần hướng dẫn giải bài tập SGK Ôn tập chương 2: Số nguyên sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 6 Tập một.
Mục lục nội dung
1. Giải bài 107 trang 98 SGK Toán 6 tập 1
2. Giải bài 108 trang 98 SGK Toán 6 tập 1
3. Giải bài 109 trang 98 SGK Toán 6 tập 1
4. Giải bài 110 trang 99 SGK Toán 6 tập 1
5. Giải bài 111 trang 99 SGK Toán 6 tập 1
6. Giải bài 112 trang 99 SGK Toán 6 tập 1
7. Giải bài 113 trang 99 SGK Toán 6 tập 1
8. Giải bài 114 trang 99 SGK Toán 6 tập 1
9. Giải bài 115 trang 99 SGK Toán 6 tập 1
10. Giải bài 116 trang 99 SGK Toán 6 tập 1
11. Giải bài 117 trang 99 SGK Toán 6 tập 1
12. Giải bài 118 trang 99 SGK Toán 6 tập 1
13. Giải bài 119 trang 100 SGK Toán 6 tập 1

1. Giải bài 107 trang 98 SGK Toán 6 tập 1
Trên trục số cho hai điểm a, b (h.53). Hãy:
a) Xác định các điểm –a; –b trên trục số;
b) Xác định các điểm |a|, |b|, |-a|, |-b|trên trục số;
c) So sánh các số a, b, –a; –b, |a|, |b|, |-a|, |-b| với 0.
Phương pháp giải
Sử dụng:
- Trên trục số: Số nằm bên phải số 0 là một số dương và số nằm bên trái số 0 là một số âm
- \(a\) và \(-a\) là hai số đối nhau (tức cùng cách điểm 0 một khoảng bằng nhau nhưng nằm về hai phía của điểm 0)
- \( \left| a \right| = \left\{ \begin{array}{l} a\,\,khi\,\,a \ge 0\\ - a\,\,khi\,\,a < 0 \end{array} \right.\)
Hướng dẫn giải
Ta có: \(\left| a \right| = \left| { - a} \right|,\left| b \right| = \left| { - b} \right|\)
Vì a ở bên trái số 0 ⇒ a là số nguyên âm nên a < 0.
b ở bên phải số 0 ⇒ b là số nguyên dương hay b>0
Từ đó ta có:
\(a < 0; - b < 0; b >0 ; - a > 0 ;\)
\( 0 < \left| { - a} \right| = \left| a \right|,0 < \left| { - b} \right| = \left| b\right|\)
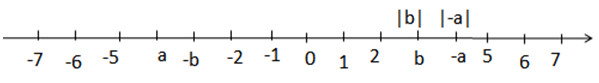
2. Giải bài 108 trang 98 SGK Toán 6 tập 1
Cho số nguyên a khác 0. So sánh -a với a, -a với 0
Phương pháp giải
- Mọi số nguyên dương đều lớn hơn số 0.
- Mọi số nguyên âm đều nhỏ hơn số 0.
- Mọi số nguyên âm đều nhỏ hơn bất kỳ số nguyên dương nào.
Hướng dẫn giải
- Nếu a > 0 thì –a < 0 và –a < a.
- Nếu a < 0 thì –a > 0 và –a > a.
3. Giải bài 109 trang 98 SGK Toán 6 tập 1
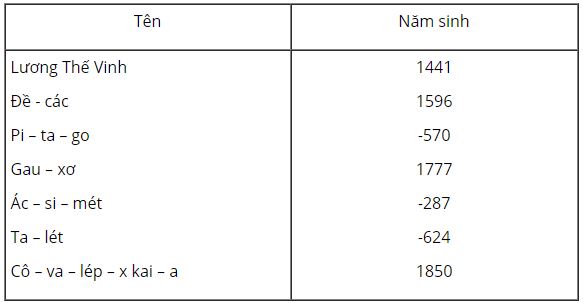
Dưới đây là tên và năm sinh của một số nhà toán học:
Sắp xếp các năm sinh trên đây theo thứ tự thời gian tăng dần.
Phương pháp giải
- Mọi số nguyên dương đều lớn hơn số 0.
- Mọi số nguyên âm đều nhỏ hơn số 0.
- Mọi số nguyên âm đều nhỏ hơn bất kỳ số nguyên dương nào.
Hướng dẫn giải
Ta có:
\(-624 < -570 < -287 \)\(< 1441 < 1596 < 1777 < 1850\)
Vậy năm sinh được sắp xếp theo thứ tự thời gian tăng dần là:
\(-624; -570; -287; 1441; 1596; 1777; 1850\)
4. Giải bài 110 trang 99 SGK Toán 6 tập 1
Trong các câu sau đây, câu nào đúng, câu nào sai ? Cho ví dụ minh họa đối với các câu sai :
a) Tổng của hai số nguyên âm là một số nguyên âm.
b) Tổng của hai số nguyên dương là một số nguyên dương.
c) Tích của hai số nguyên âm là một số nguyên âm.
d) Tích của hai số nguyên dương là một số nguyên dương.
Phương pháp giải
Lưu ý: Tích của chẵn thừa số nguyên âm là một số nguyên dương
Hướng dẫn giải
Câu a:
Tổng của hai số nguyên âm là một số nguyên âm: Đúng;
Câu b:
Tổng của hai số nguyên dương là một số nguyên dương: Đúng;
Câu c:
Tích của hai số nguyên âm là một số nguyên âm: Sai vì tích của hai số nguyên âm là số nguyên dương.
Ví dụ: \((-7).(-5) = 35.\)
Câu d:
Tích của hai số nguyên dương là một số nguyên dương: Đúng.
5. Giải bài 111 trang 99 SGK Toán 6 tập 1
Tính các tổng sau:
a) \( [(-13) + (-15)] + (-8) \)
b) \( 500 – (-200) – 210 - 100\)
c) \( –(-129) + (-119) - 301 + 12\)
d) \( 777 – (-111) –(-222) + 20\)
Phương pháp giải
- Sử dụng tính chất giao hoán \(a+b=b+a\), tính chất kết hợp \((a+b)+c=a+(b+c)\), và quy tắc phá ngoặc.
Lưu ý: \(- (-a) = a\) \(- a + (-b) = - (a + b)\)
Hướng dẫn giải
Câu a:
\((–13 ) + (–15) + (–8)\)
\(= – (13 + 15 + 8)\)
\(= –36.\)
Câu b:
\(500 – (–200 ) – 210 – 100\)
\(= 500 + 200 – 210 – 100\)
\(= 500 + 200 – (210 + 100)\)
\(= 700 – 310 = 390.\)
Câu c:
\(–(–129) + (–119) – 301 + 12\)
\(= 129 – 119 – 301 + 12\)
\(= (129 + 12) – (119 + 301)\)
\(= 141 – 420\)
\(= –279.\)
Câu d:
\(777 – (–111) – (–222) + 20\)
\(= 777 + 111 + 222 + 20\)
\(= (777 + 111 + 222) + 20\)
\(= 1110 + 20 = 1130. \)
6. Giải bài 112 trang 99 SGK Toán 6 tập 1
Đố vui: Bạn Điệp đã tìm được hai số nguyên, số thứ nhất (2a) bằng hai lần số thứ hai (a) nhưng số thứ hai trừ đi 10 lại bằng số thứ nhất trừ đi 5 (tức là a – 10 = 2a – 5). Hỏi đó là hai số nào?
Phương pháp giải
Khi chuyển một số hạng tử từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu + thành dấu - và dấu - đổi thành dấu +.
Hướng dẫn giải
Số thứ nhất: \(2a\)
Số thứ hai: \(a\)
Theo đề bài: \(a - 10 = 2a - 5\)
Chuyển \(a\) từ vế trái sang vế phải, chuyển \(-5\) từ vế phải sang vế trái ta được:
\(-10 + 5 = 2a - a\)
Hay \(-5 = a\) suy ra \(a = -5\)
Do đó: \(2a=2.(-5)=-10\)
Vậy số thứ nhất là: \(-10 ;\) số thứ hai là: \(-5.\)
7. Giải bài 113 trang 99 SGK Toán 6 tập 1
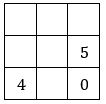
Đố: Hãy điền các số 1, -1, 2, -2, 3, -3 vào các ô trống ở hình vuông bên (mỗi số vào một ô) sao cho tổng ba số trên mỗi dòng, mỗi cột hoặc mỗi đường chéo đều bằng nhau.
Phương pháp giải
- Tính tổng ở mỗi hàng (mỗi cột) sau khi đã điền đủ các số từ đó tìm các số còn thiếu ở mỗi hàng, mỗi cột.
- Sử dụng qui tắc cộng trừ các số nguyên.
- Muốn cộng hai số nguyên khác dấu không đối nhau, ta tìm hiệu các giá trị tuyệt đối của chúng (số lớn trừ số nhỏ) rồi đặt trước kết quả tìm được dấu của hai số có giá trị tuyệt đối lớn hơn.
- Muốn cộng hai số nguyên âm ta cộng hai giá trị tuyệt đối của chúng rồi đặt dấu "-" trước kết quả.
- Muốn trừ số nguyên a cho số nguyên b ta cộng a với số đối của b.
Hướng dẫn giải
Tổng tất cả các số ở trong bảng là : \(1 + (–1) + 2 + (–2) \)\(+ 3 + (–3) + 0 + 4 + 5 = 9.\)
Tổng các số trên mỗi hàng, mỗi cột bằng nhau nên tổng các số ở mỗi hàng, mỗi cột bằng \(9 : 3 = 3.\)
Từ đó: \(5 + 0 + (c) = 3,\) suy ra \((c) = 3 – 0 – 5 = –2.\)
\(4 + (e) + (c) = 3,\) suy ra \((e) = 3 – 4 – (c) \)\(= 3 – 4 – (–2) = 1.\)
\(5 + (d) + (e) = 3,\) suy ra \((d) = 3 – 5 – (e)\)\( = 3 – 5 – 1 = –3.\)
\(4 + (d) + (a) = 3,\) suy ra \((a) = 3 – 4 – (d)\)\( = 3 – 4 – (–3) = 2.\)
\(4 + (f) + 0 = 3,\) suy ra \((f) = 3 – 4 – 0 = –1.\)
\((a) + (b) + (c) = 3,\) suy ra \((b) = 3 – (a) – (c) \)\(= 3 – 2 – (–2) = 3.\)
Từ đó ta có bảng kết quả như sau:
8. Giải bài 114 trang 99 SGK Toán 6 tập 1
Liệt kê và tính tổng tất cả các số nguyên \(x\) thỏa mãn:
a) \(- 8 < x < 8\)
b) \(- 6 < x < 4\)
c) \(- 20 < x < 21\)
Phương pháp giải
- Liệt kê các số thỏa mãn đề bài và tính tổng bằng cách nhóm các số đối nhau để tính nhanh.
- Sử dụng: Hai số đối nhau có tổng bằng \(0\)
Hướng dẫn giải
Câu a:
Các số tự nhiên lớn hơn –8 và nhỏ hơn 8 là:
\(x ∈ \{–7; –6; –5; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5; 6; 7\}.\)
Tính tổng các số :
\((–7) + (–6) + (–5) + (–4) + (–3)\)\( + (–2) + (–1) + 0 + 1 + 2 + 3 \)\(+ 4 + 5 + 6 + 7\)
\(= ( (-7)+ 7) + ( (-6) + 6) + ( (-5) + 5)\)\( + ( (-4) + 4) + ( (-3) + 3 ) + \)\(( (-2) + 2) + ( (-1) +1) + 0\)
\(= 0 + 0 + 0 + 0 \)\(+ 0 + 0 + 0 + 0 = 0.\)
Câu b:
Các số tự nhiên lớn hơn –6 và nhỏ hơn 4 là :
\(x ∈ \{–5; –4; –3; –2; –1; 0; 1; 2; 3\}.\)
Tổng các số này là
\((-5) + (-4) + (-3) + (-2)\)\( + (-1) + 0 + 1+ 2+ 3\)
\(= - 9 + ( (-3) + 3) \)\(+ ( (-2) + 2) \)\(+ ( (-1) + 1) + 0\)
\(= - 9+0+0+0+0=-9\)
Câu c:
Các số tự nhiên lớn hơn –20 và nhỏ hơn 21 là:
\(x ∈ \{20; ±19; ±18; ±17; ...; ±3; ±2; ±1; 0\}.\)
Tổng các số trên bằng 20.
Vì \((-19) + 19 + (-18) + 18\)\( +... + (-1) + 1 + 0 + 20 = 20\)
9. Giải bài 115 trang 99 SGK Toán 6 tập 1
Tìm a ∈ Z, biết:
a) |a| = 5 b) |a| = 0
c) |a| = -3 d) |a| = |-5|
e) -11|a| = -22
Phương pháp giải
a) \(\left| x \right| = a\) suy ra \(x=a\) hoặc \(x=-a\)
b) Giá trị tuyệt đối của số 0 là số 0.
c) Giá trị tuyệt đối của một số khác 0 luôn là số dương.
d) (\left| x \right| = a\) suy ra \(x=a\) hoặc \(x=-a\)
e) Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.
Hướng dẫn giải
Câu a:
\(|a| = 5\) suy ra \(a = 5\) hoặc \(a = -5\)
Câu b:
\(|a| = 0\) suy ra \(a = 0\)
Câu c:
\(|a| = -3\) không tìm được số \(a\) vì \(|a|\) không thể là số âm.
Câu d:
\(|a| = |-5|\) suy ra \(|a| = 5.\) Khi đó \(a = 5\) hoặc \(a = -5\)
Câu e:
\(-11|a| = -22\)
\(|a| = (-22):(-11)\)
\(|a| = 2\)
Suy ra: \(a = 2\) hoặc \(a = -2\)
10. Giải bài 116 trang 99 SGK Toán 6 tập 1
Tính:
a) \((-4).(-5).(-6)\)
b) \((-3 + 6).(-4)\)
c) \((-3 - 5) .(-3 + 5)\)
d) \((-5 - 13):(-6)\)
Phương pháp giải
- Tính trong ngoặc trước rồi thực hiện phép nhân.
- Muốn nhân hai số nguyên khác dấu, ta nhân hai giá trị tuyệt đối của chúng rồi đặt dấu "-" trước kết quả nhận được.
- Muốn nhân hai số nguyên cùng dấu, ta nhân hai giá trị tuyệt đối của chúng.
- Cách nhận biết dấu của tích:
(+) . (+) => (+)
(-) . (-) => (+)
(+). (-) => (-)
(-) . (+) => (-)
Hướng dẫn giải
Câu a:
\((-4) . (-5) . (-6) \)\(=-(4 . 5 . 6) = -120;\)
Câu b:
\((-3 + 6) . (-4) \)\(= 3 . (-4) = - (3 . 4) = -12\)
Câu c:
\((-3 -5) . (-3 + 5)\)\( = (-8) .2 = -(8 . 2) = -16;\)
Câu d:
\((-5 - 13) : (-6) \)\(= (-18) : (-6) = 18 : 6 = 3.\)
11. Giải bài 117 trang 99 SGK Toán 6 tập 1
Tính:
a) \({\left( { - 7} \right)^3}{.2^4}\)
b) \({5^4}.{\left( { - 4} \right)^2}\)
Phương pháp giải
\({a^n} = \underbrace {a.a.a...a}_{n\,\,thừa\,\,số\,\,\,a}\)
Hướng dẫn giải
Câu a:
\({\left( { - 7} \right)^3}{.2^4} = \left( { - 7} \right).\left( { - 7} \right).\left( { - 7} \right).2.2.2.2\)
\(= - 343.16 = - 5488\)
Câu b:
\(\begin{array}{l}
{5^4}.{\left( { - 4} \right)^2}\\
= 5.5.5.5.\left( { - 4} \right).\left( { - 4} \right)\\
= 25.25.\left( { - 4} \right).\left( { - 4} \right)\\
= 25.\left( { - 4} \right).25.\left( { - 4} \right)\\
= - 100.\left( { - 100} \right)\\
= 10000
\end{array}\)
12. Giải bài 118 trang 99 SGK Toán 6 tập 1
Tìm số nguyên \(x\), biết:
a) \(2x - 35 = 15\);
b) \(3x + 17 = 2\);
c) \(|x - 1| = 0\)
Phương pháp giải
a) Số bị trừ bằng hiệu cộng với số trừ
b) Số hạng chưa biết bằng tổng trừ đi số hạng đã biết
c) \(\left| x \right| = 0\) suy ra \(x=0\)
Hoặc sử dụng quy tắc chuyển vế:
Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu "+" đổi thành dấu "−" và dấu "−" thành dấu "+".
Hướng dẫn giải
Câu a:
\(2x - 35 = 15\)
\( 2x = 15 + 35\) (chuyển \(-35\) sang vế phải)
\(2x = 50\)
\(x = 50:2\)
\(x = 25\)
Vậy \(x = 25\).
Câu b:
\(3x + 17 = 2 \)
\(3x = 2 - 17 \) (chuyển \(17\) sang vế phải)
\(3x = -15\)
\(x = -15:3\)
\(x = -5\)
Vậy \(x = -5\).
Câu c:
\(|x - 1| = 0\)
\(x - 1 = 0\)
\( x = 0 + 1\) (chuyển \(-1\) sang vế phải)
\(x = 1\)
Vậy \(x = 1\).
13. Giải bài 119 trang 100 SGK Toán 6 tập 1
Tính bằng hai cách:
a) 15.12 – 3.5.10;
b) 45 – 9.(13+5);
c) 29.(19 – 13) – 19. (29 – 13).
Phương pháp giải
Cách 1: Ta thực hiện phép tính trong ngoặc trước, ngoài ngoặc sau; nếu không có ngoặc thì nhân chia trước, cộng trừ sau.
Cách 2: Sử dụng tính chất phân phối của phép nhân đối với phép cộng hoặc phép trừ:
\(a. (b + c) = a.b + a. c\)
Hoặc \(a. (b - c) = a.b - a.c\)
Hướng dẫn giải
Câu a:
Cách 1:
\(15.12 – 3.5.10 \\= 180 - 150 = 30\)
Cách 2:
\(15.12 – 3.5.10 \\= 15.12 – 15.10\\ = 15.(12 - 10) \\= 15.2 = 30\)
Câu b:
Cách 1:
\(45 – 9.(13 + 5) \\= 45 – 9.18 \\= 45 - 162 \\= - (162 - 45) \\= -117\)
Cách 2:
\(45 – 9.(13 + 5)\\= 9.5 – (9.13 + 9.5) \\= 9.5 – 9.13 – 9.5 \\= 9.5 – 9.5 – 9.13\)
\(= - 9.13 \\= -117\)
Câu c:
Cách 1:
\(29.(19 - 13) – 19.(29 - 13) \\= 29.6 – 19.16 \\= 174 – 304 \\= - (304 - 174) \\= -130\)
Cách 2:
\(29.(19 - 13) – 19.(29 - 13) \)\(= 29.19 - 29.13 - (19.29 -19.13)\)
\(= 29.19 - 29.13 - 19.29 +19.13\)
\(= 29.19 - 29.19 - 29.13 + 19.13 \)\(=0+ 13.(-29 + 19)\)
\(= 13.(-10)\)\( = -130\)
14. Giải bài 120 trang 100 SGK Toán 6 tập 1
Cho hai tập hợp: \(A =\{3; -5; 7\}; B = \{-2; 4; -6; 8\}\).
a) Có bao nhiêu tích \(ab\) (với \(a ∈ A\) và \(b ∈ B\)) được tạo thành?
b) Có bao nhiêu tích lớn hơn \(0\), bao nhiêu tích nhỏ hơn \(0\)?
c) Có bao nhiêu tích là bội của \(6\)?
d) Có bao nhiêu tích là ước của \(20\)?
Phương pháp giải
Cách nhận biết dấu của tích:
(+) . (+) \(\to\) (+)
(-) . (-) \(\to\) (+)
(+). (-) \(\to\) (-)
(-) . (+) \(\to\) (-)
Hướng dẫn giải
Câu a:
Các tích \(ab\) (với \(a ∈ A\) và \(b ∈ B\)) là:
\(3 . (–2); 3 . 4; 3 . (–6); 3 . 8;\)
\((–5) . (–2); (–5) . 4; (–5) . (–6); (–5) . 8;\)
\(7 . (–2); 7 . 4; 7 . (–6); 7 . 8.\)
Vậy có tất cả 12 tích.
Câu b:
Các tích lớn hơn 0 là các tích có hai thừa số cùng dấu. Đó là:
\(3 . 4; 3 . 8;\)
\((–5) . (–2); (–5) . (–6);\)
\(7.4; 7.8\)
Có tất cả 6 tích dương.
Còn lại các tích âm là: \(12 - 6 = 6\) tích.
Câu c:
Các tích là bội của 6 là:
\(3 . (–2); 3 . 4; 3 . (–6) ;\) \(3 . 8 ; (–5) . (–6) ; 7 . (–6)\)
Có tất cả 6 tích là bội của 6.
d) Có 2 tích là ước của 20 là : \((–5) . 4\) và \((–5) . (–2)\)
15. Giải bài 121 trang 100 SGK Toán 6 tập 1
Đố: Hãy điền các số nguyên thích hợp vào các ô trống trong bảng dưới đây sao cho tích cho ba số ở ba ô liền nhau đều bằng 120:
Phương pháp giải
Lập luận để tìm ra qui luật: các số ở cách nhau 2 ô đều bằng nhau từ đó điền các số còn thiếu vào mỗi ô trống.
Hướng dẫn giải
Cách làm như sau: gọi 3 số còn lại trong 4 ô đầu tiên lần lượt là \(a, b, c\) như hình dưới:
Tích 3 ô đầu tiên là: \(a.b.6\)
Tích 3 ô thứ hai là: \(b.6.c\)
Theo bài, tích 3 số ở ba ô liên tiếp đều bằng \(120\) nên:
\(a.b.6 = b.6.c => a = c\)
Từ đó ta tìm ra qui luật: các số ở cách nhau 2 ô đều bằng nhau. Ta điền \(6\) và \(-4\) vào bảng, như sau:
Vậy số còn lại bằng \((-5)\) vì: \((-5).(-4).6 = 120.\)
Tham khảo thêm
- doc Giải bài tập SGK Toán 6 Bài 1: Làm quen với số nguyên âm
- doc Giải bài tập SGK Toán 6 Bài 2: Tập hợp các số nguyên
- doc Giải bài tập SGK Toán 6 Bài 3: Thứ tự trong tập hợp các số nguyên
- doc Giải bài tập SGK Toán 6 Bài 4: Cộng hai số nguyên cùng dấu
- doc Giải bài tập SGK Toán 6 Bài 5: Cộng hai số nguyên khác dấu
- doc Giải bài tập SGK Toán 6 Bài 6: Tính chất của phép cộng các số nguyên
- doc Giải bài tập SGK Toán 6 Bài 7: Phép trừ hai số nguyên
- doc Giải bài tập SGK Toán 6 Bài 8: Quy tắc dấu ngoặc
- doc Giải bài tập SGK Toán 6 Bài 9: Quy tắc chuyển vế
- doc Giải bài tập SGK Toán 6 Bài 10: Nhân hai số nguyên khác dấu
- doc Giải bài tập SGK Toán 6 Bài 11: Nhân hai số nguyên cùng dấu
- doc Giải bài tập SGK Toán 6 Bài 12: Tính chất của phép nhân
- doc Giải bài tập SGK Toán 6 Bài 13: Bội và ước của một số nguyên



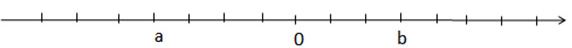
.JPG)
.JPG)

.JPG)
.JPG)
.JPG)
