Giải bài tập SGK Toán 6 Bài 13: Bội và ước của một số nguyên
Phần hướng dẫn giải bài tập SGK Bội và ước của một số nguyên sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 6 Tập một.
Mục lục nội dung

1. Giải bài 101 trang 97 SGK Toán 6 tập 1
Tìm năm bội của: \(3; -3.\)
Phương pháp giải
Tổng quát: Muốn tìm bội của 1 số nguyên a bất kỳ ta lấy a nhân với các số: 0, -1, 1, 2, -2....kết quả tìm được chính là bội của số nguyên a.
Hướng dẫn giải
Có thể chọn năm bội của \(3\) là \(-6; -3; 0; 3; 6\) và năm bội của \(-3\) là \(-6; -3; 0; 3; 6.\)
Bài này có rất nhiều đáp án, tùy theo cách bạn chọn các bội của hai số này.
2. Giải bài 102 trang 97 SGK Toán 6 tập 1
Tìm tất cả các ước của: \(-3; 6; 11; -1.\)
Phương pháp giải
+ Cho \(a,b\in \mathbb Z\) và \( b\ne 0\). Nếu có số nguyên \(q\) sao cho \(a=b.q\) thì ta nói \(a\) chia hết cho \(b.\) Khi đó, \(a\) là bội của \(b\) và \(b\) là ước của \(a.\)
+ Nếu số nguyên b là ước của số nguyên a thì –b cũng là ước của số nguyên a.
+ Nếu b là ước của a thì b cũng là ước của |a| và ngược lại.
+ Để tìm các ước của một số nguyên a, ta chỉ cần tìm các ước dương của |a| rồi thêm các số đối của chúng thì ta được các ước của số nguyên a.
Hướng dẫn giải
Các ước nguyên dương của 3 là 1; 3.
Do đó \(Ư(–3) = \{1; 3; –1; –3\}\)
Các ước nguyên dương của 6 là 1 ; 2 ; 3 ; 6.
Do đó \(Ư(6) = \{1 ; 2 ; 3 ; 6 ; –1; –2; –3; –6\}\)
Các ước nguyên dương của 11 là : 1 ; 11
Do đó \(Ư(11) = \{1 ; 11 ; –1; –11\}\)
Các ước nguyên dương của 1 là 1.
Do đó \(Ư(–1) = \{1; –1\}\)
3. Giải bài 103 trang 97 SGK Toán 6 tập 1
Cho hai tập hợp số \(A = \{2; 3; 4; 5; 6\},\) \(B = \{21; 22; 23\}.\)
a) Có thể lập được bao nhiêu tổng dạng \((a + b)\) với \(a ∈ A\) và \(b ∈ B ?\)
b) Trong các tổng trên có bao nhiêu tổng chia hết cho \(2\) ?
Phương pháp giải
a) Lấy mỗi phần tử \(a ∈ A\) cộng với một phần tử \(b ∈ B\) ta được một tổng \(a + b.\)
b) Mỗi số chẵn thuộc \(A\) cộng với một số chẵn thuộc \(B\) ta được một tổng chia hết cho \(2\) và mỗi số lẻ thuộc \(A\) cộng với một số lẻ thuộc \(B\) cũng được một số chia hết cho \(2.\)
Hướng dẫn giải
Câu a
Mỗi phần tử \(a ∈ A\) cộng với một phần tử \(b ∈ B\) ta được một tổng \(a + b\) nên các tổng \(a+b\) là:
\(2 + 21 ; 3 + 21 ; 4 + 21 ; 5 + 21 ; 6 + 21\)
\(2 + 22 ; 3 + 22 ; 4 + 22 ; 5 + 22 ; 6 + 22\)
\(2 + 23 ; 3 + 23 ; 4 + 23 ; 5 + 23 ; 6 + 23\)
Có tất cả 15 tổng dạng trên.
Câu b
Trong các tổng trên, tổng nào có các số hạng cùng là số chẵn hoặc cùng là số lẻ sẽ chia hết cho 2.
Các tổng có hai số đều chẵn là: \(2 + 22 ; 4 + 22 ; 6 + 22\)
Các tổng có hai số đều lẻ là: \(3 + 21 ; 5 + 21 ;3 + 23 ; 5 + 23\)
Có tất cả 7 tổng chia hết cho 2 như trên.
4. Giải bài 104 trang 97 SGK Toán 6 tập 1
Tìm số nguyên x, biết:
a) \(15x = -75\); b) \(3\left| x \right| = 18\)
Phương pháp giải
a) Áp dụng: \(a.b = c \) thì \(b = c : a\)
b) Áp dụng \(\left| x \right| = a\) thì \(x=a\) hoặc \(x=-a.\)
Hướng dẫn giải
Câu a
\(\begin{array}{l}
15x = - 75\\
x = \left( { - 75} \right):15\\
x = - 5
\end{array}\)
Câu b
\(\begin{array}{l}
3\left| x \right| = 18\\
\left| x \right| = 18:3\\
\left| x \right| = 6
\end{array}\)
Nên \(x = 6\) hoặc \(x = -6\)
Đáp số: a) \(x = -5\)
b) \(x = 6; x = -6\)
5. Giải bài 105 trang 97 SGK Toán 6 tập 1
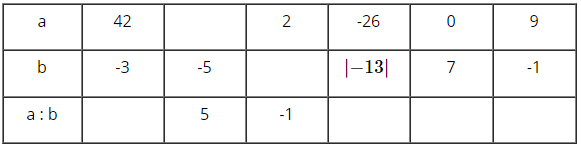
Điền số vào ô trống cho đúng:
Phương pháp giải
Áp dụng:
\(a : b = c\) thì \(a = b. c;\)
\(a: b = c\) thì \(b = a : c\)
+ Nếu số bị chia và số chia cùng dấu thì thương mang dấu dương.
+ Nếu số bị chia và số chia trái dấu thì thương mang dấu âm.
Chú ý:
\(\left| a \right| = \left\{ \begin{array}{l}
a\,\,khi\,\,a \ge 0\\
- a\,\,khi\,\,a < 0
\end{array} \right.\)
Hướng dẫn giải
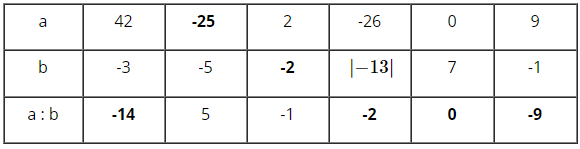
+) Với \(a=42;b=-3\) thì \(a:b=42:(-3)=-14\)
+) Với \(b=-5;a:b=5\) thì \(a=5.b=5.(-5)=-25\)
+) Với \(a=2;a:b=-1\) thì \(b=a:(-1)=2:(-1)=-2\)
+) Với \(b=|-13|=13;a=-26\) thì \(a:b=(-26):13=-2\)
+) Với \(a=0;b=7\) thì \(a:b=0:7=0\)
+) Với \(a=9;b=-1\) thì \(a:b=9:(-1)=-9\)
Ta có bảng sau:
6. Giải bài 106 trang 97 SGK Toán 6 tập 1
Có hai số nguyên a, b khác nhau nào mà a \(\vdots\) b và b \(\vdots\) a không ?
Phương pháp giải
Cho \(a,b\in \mathbb Z\) và \(b\ne 0\). Nếu có số nguyên \(q\) sao cho \(a=bq\) thì ta nói \(a\) chia hết cho \(b.\)
Chú ý đến hai số nguyên đối nhau.
Hướng dẫn giải
Các số nguyên đối nhau thì chia hết cho nhau.
Ví dụ:
\(6 \,⋮\, (– 6)\) và \((– 6) \,⋮\, 6;\)
\(15 \,⋮\, (– 15)\) và \((– 15) \,⋮\, 15 ;\)
Chứng minh: "Nếu a \(\vdots\) b và b \(\vdots\) a thì a và b là hai số nguyên đối nhau."
Vì \(a \,\,⋮\, \,b\) nên tồn tại số nguyên \(k\) để \(a = k . b\)
Vì \(b\, \,⋮\, \,a\) nên tồn tại số nguyên \(m\) để \(b = m . a.\)
Từ đó \(b = m . a = m . k . b\) (vì \(a = k . b\))
Suy ra \(m . k = 1 .\)
Mà \(m\) và \(k\) là các số nguyên nên có 2 trường hợp:
+) \( m = k = 1\) thì \(a = b\) (loại).
+) \(m = k = –1\) thì \(a = –b\) và \(b = –a\) hay \(a\) và \(b\) là hai số nguyên đối nhau.
Tham khảo thêm
- doc Giải bài tập SGK Toán 6 Bài 1: Làm quen với số nguyên âm
- doc Giải bài tập SGK Toán 6 Bài 2: Tập hợp các số nguyên
- doc Giải bài tập SGK Toán 6 Bài 3: Thứ tự trong tập hợp các số nguyên
- doc Giải bài tập SGK Toán 6 Bài 4: Cộng hai số nguyên cùng dấu
- doc Giải bài tập SGK Toán 6 Bài 5: Cộng hai số nguyên khác dấu
- doc Giải bài tập SGK Toán 6 Bài 6: Tính chất của phép cộng các số nguyên
- doc Giải bài tập SGK Toán 6 Bài 7: Phép trừ hai số nguyên
- doc Giải bài tập SGK Toán 6 Bài 8: Quy tắc dấu ngoặc
- doc Giải bài tập SGK Toán 6 Bài 9: Quy tắc chuyển vế
- doc Giải bài tập SGK Toán 6 Bài 10: Nhân hai số nguyên khác dấu
- doc Giải bài tập SGK Toán 6 Bài 11: Nhân hai số nguyên cùng dấu
- doc Giải bài tập SGK Toán 6 Bài 12: Tính chất của phép nhân
- doc Giải bài tập SGK Toán 6 Ôn tập chương 2: Số nguyên