Giải bài tập SGK Toán 6 Bài 7: Phép trừ hai số nguyên
Phần hướng dẫn giải bài tập SGK Phép trừ hai số nguyên sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 6 Tập một.
Mục lục nội dung
1. Giải bài 47 trang 82 SGK Toán 6 tập 1
2. Giải bài 48 trang 82 SGK Toán 6 tập 1
3. Giải bài 49 trang 82 SGK Toán 6 tập 1
4. Giải bài 50 trang 82 SGK Toán 6 tập 1
5. Giải bài 51 trang 82 SGK Toán 6 tập 1
6. Giải bài 52 trang 82 SGK Toán 6 tập 1
7. Giải bài 53 trang 82 SGK Toán 6 tập 1
8. Giải bài 54 trang 83 SGK Toán 6 tập 1

1. Giải bài 47 trang 82 SGK Toán 6 tập 1
\(2 - 7\); \(1 - (-2)\);
\((-3) - 4\); \((-3) - (-4)\).
Phương pháp giải
Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối của b.
\( a - b = a + (-b)\)
Hướng dẫn giải
\(2 - 7 = 2 + (-7) = - ( 7 - 2) = -5\);
\(1 - (-2) = 1 + 2 = 3\);
\((-3) - 4 = (-3) + (-4)= - ( 3 + 4) = -7\);
\((-3) - (-4) = (-3) + 4 = 4 - 3 = 1\).
2. Giải bài 48 trang 82 SGK Toán 6 tập 1
Tính
\( 0 - 7 = ?; \) \( 7 - 0 = ?; \)
\( a - 0 = ?; \) \( 0 - a = ?.\)
Phương pháp giải
Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối của b: \(a-b=a+(-b)\)
Hướng dẫn giải
\(0 - 7 = 0 + (-7) = -(7-0)= -7; \)
\( 7 - 0 = 7 + 0 = 7;\)
\(a - 0 = a + 0 = a; \)
\(0 - a = 0 + (-a) = -a.\)
3. Giải bài 49 trang 82 SGK Toán 6 tập 1
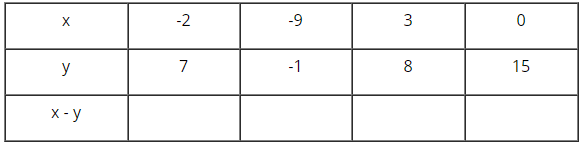
Điền số thích hợp vào ô trống:
Phương pháp giải
Số đối của \(a\) là \(- a\).
Ví dụ số đối của \(2\) là \(- 2\) và ngược lại.
Hướng dẫn giải
a và –a là số đối của nhau.
Số đối của –15 là 15;
Số đối của –2 là 2;
Số đối của 0 là 0;
Số đối của –(–3) là –3.
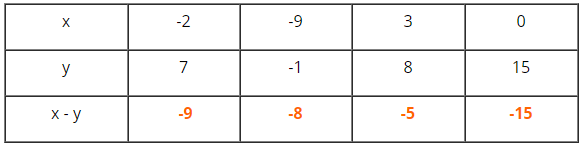
Ta điền như sau:
4. Giải bài 50 trang 82 SGK Toán 6 tập 1
Dùng các số 2, 9 và các phép toán "+", "-" điền vào các ô trống trong bảng sau đây để được bảng tính đúng. Ở mỗi dòng hoặc mỗi cột, mỗi số hoặc phép tính chỉ được dùng một lần:
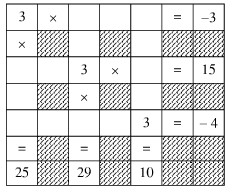
Phương pháp giải
Lưu ý đến thứ tự thực hiện phép tính: nhân chia trước, cộng trừ sau.
Hướng dẫn giải
Điền vào bảng như sau:
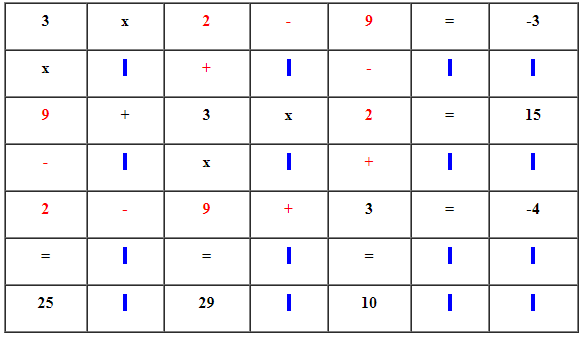
Bằng cách thử trực tiếp số \(2\) và số \(9\) vào cột ba ta có:
\(2-3\times 9 \ne 29\)
\(9 + 3 \times 2 \ne 29\)
\(2+3\times 9 =29\) (đúng)
\(9-3\times 2\ne 29\).
Như vậy ở cột ba là: \(2+3\times 9 =29\)
Khi đó ở dòng một sẽ là: \(3\times 2-9=-3\).
Dòng năm phải là: \(2-9+3=-4\).
Suy ra cột một là: \(3\times 9-2=25\).
Từ đó suy ra được dòng ba và cột năm.
5. Giải bài 51 trang 82 SGK Toán 6 tập 1
Tính:
a) \( 5 - (7 - 9); \) b) \( (-3) - (4 - 6)\).
Phương pháp giải
+ Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối b.
\(a -b = a + (-b)\)
+ Thứ tự thực hiện phép tính với số nguyên giống với thứ tự thực hiện phép tính với số tự nhiên:
Với biểu thức không có dấu ngoặc: Nhân và chia → cộng và trừ.
Với biểu thức có dấu ngoặc: ( ) → [ ] → { }
Hướng dẫn giải
Thực hiện phép tính trong dấu ngoặc trước.
Câu a
\( 5 - (7 - 9) = 5 - [ 7 + (- 9) ] = 5 - [ - ( 9 - 7) ]\)
\(= 5 - (- 2) = 5 + 2 = 7\);
Câu b
\((-3) - (4 - 6) = (- 3) - [ 4 + (-6)] \)
\(= (- 3) - [ - ( 6 - 4)]\)
\(= (- 3) - (- 2) = ( -3) + 2 \)
\(= - ( 3 - 2 ) = - 1.\)
6. Giải bài 52 trang 82 SGK Toán 6 tập 1
Tính tuổi thọ của nhà bác học Ác-si-mét, biết rằng ông sinh năm \(-287\) và mất năm \(-212.\)
Phương pháp giải
Muốn tính tuổi thọ ta lấy năm mất trừ đi năm sinh.
Hướng dẫn giải
Tuổi thọ của nhà bác học Ác-si-mét là:
\(-212 - (-287) = -212 + 287 = 287 - 212 = 75\) (tuổi)
Vậy nhà bác học Ác-si-mét thọ \(75\) tuổi.
7. Giải bài 53 trang 82 SGK Toán 6 tập 1
Điền số thích hợp vào ô trống:
Phương pháp giải
Muốn trừ số nguyên \(a\) cho số nguyên \(b\), ta cộng \(a\) với số đối \(b\).
\(a -b = a + (-b)\)
Hướng dẫn giải
+) \(-2 - 7 = -2 + (-7) \)\(= -(2 + 7) = -9 \)
+) \(-9 - (-1) = -9 + 1 \)\(= - (9-1) = -8\)
+) \(3 - 8 = 3 + (-8) \)\(= - (8 - 3 )= -5\)
+) \(0 - 15 = 0 + (-15) \)\(= -(15 - 0) = -15\)
8. Giải bài 54 trang 83 SGK Toán 6 tập 1
Tìm số nguyên x, biết:
a) \(2 + x = 3\);
b) \(x + 6 = 0\);
c) \( x + 7 = 1\).
Phương pháp giải
x trong bài toán đóng vai trò là số hạng chưa biết.
Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.
Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối b.
\(a -b = a + (-b)\)
Hướng dẫn giải
Câu a
\(2 + x = 3\)
\(x = 3-2\)
\(x = 1\)
Vậy \(x = 1\)
Câu b
\(x + 6 = 0\)
\(x = 0 - 6\)
\(x = 0 + (-6)\)
\(x = -6\)
Vậy \(x = -6\)
Câu c
\( x + 7 = 1\)
\(x = 1-7\)
\(x = 1 + (-7)\)
\(x = -(7-1)\)
\(x = -6\)
Vậy \(x = -6.\)
9. Giải bài 55 trang 83 SGK Toán 6 tập 1
Đố vui: Ba bạn Hồng, Hoa, Lan tranh luận với nhau:
Hồng nói rằng có thể tìm được hai số nguyên mà hiệu của chúng lớn hơn số bị trừ; Hoa khẳng định rằng không thể tìm được; Lan lại nói rằng còn có thể tìm được hai số nguyên mà hiệu của chúng lớn hơn cả số bị trừ và số trừ.
Bạn đồng ý với ý kiến của ai ? Vì sao ? Cho ví dụ.
Phương pháp giải
Muốn trừ số nguyên \(a\) cho số nguyên \(b\), ta cộng \(a\) với số đối của \(b.\) \(a-b=a+(-b)\) để lập luận.
Hướng dẫn giải
Cả 2 bạn Lan và Hồng đều nói đúng.
Vì nếu phép trừ có số bị trừ là số nguyên dương, số trừ là số nguyên âm thì hiệu lớn hơn cả số trừ và số bị trừ.
Thật vậy giả sử có hai số nguyên dương \(a\) và \(b\), khi đó \(-b\) là số nguyên âm.
Ta có: \(a – (–b) = a + b.\)
Mà \(a, b\) cùng dương nên \(a + b > a\) và \(a + b > (–b).\)
Ví dụ: \( 3 - (-5) = 3 + 5 = 8\). Rõ ràng \( 8 > 3\) và \(8 > -5\).
10. Giải bài 56 trang 83 SGK Toán 6 tập 1
Sử dụng máy tính bỏ túi:
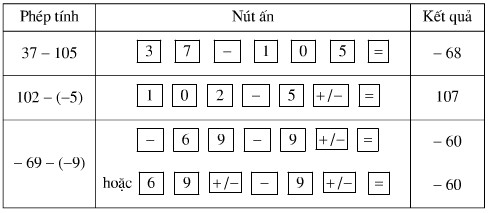
Dùng máy tính bỏ túi để tính:
a) \(169 - 733;\)
b) \(53 - (-478)\)
c) \(-135 - (-1936).\)
Hướng dẫn giải
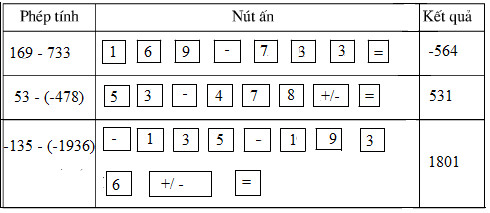
Tham khảo thêm
- doc Giải bài tập SGK Toán 6 Bài 1: Làm quen với số nguyên âm
- doc Giải bài tập SGK Toán 6 Bài 2: Tập hợp các số nguyên
- doc Giải bài tập SGK Toán 6 Bài 3: Thứ tự trong tập hợp các số nguyên
- doc Giải bài tập SGK Toán 6 Bài 4: Cộng hai số nguyên cùng dấu
- doc Giải bài tập SGK Toán 6 Bài 5: Cộng hai số nguyên khác dấu
- doc Giải bài tập SGK Toán 6 Bài 6: Tính chất của phép cộng các số nguyên
- doc Giải bài tập SGK Toán 6 Bài 8: Quy tắc dấu ngoặc
- doc Giải bài tập SGK Toán 6 Bài 9: Quy tắc chuyển vế
- doc Giải bài tập SGK Toán 6 Bài 10: Nhân hai số nguyên khác dấu
- doc Giải bài tập SGK Toán 6 Bài 11: Nhân hai số nguyên cùng dấu
- doc Giải bài tập SGK Toán 6 Bài 12: Tính chất của phép nhân
- doc Giải bài tập SGK Toán 6 Bài 13: Bội và ước của một số nguyên
- doc Giải bài tập SGK Toán 6 Ôn tập chương 2: Số nguyên