Giải bài tập SGK Toán 6 Bài 10: Nhân hai số nguyên khác dấu
Phần hướng dẫn giải bài tập SGK Nhân hai số nguyên khác dấu sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 6 Tập một.
Mục lục nội dung

1. Giải bài 73 trang 89 SGK Toán 6 tập 1
Thực hiện phép tính:
a) \((-5) . 6\); b) \(9 . (-3)\);
c) \((-10) . 11\); d) \(150 . (-4)\)
Phương pháp giải
Quy tắc nhân hai số nguyên khác dấu: Muốn nhân hai số nguyên khác dấu, ta nhân hai giá trị tuyệt đối của chúng rồi đặt dấu " -" trước kết quả nhận được.
Hãy nhớ: Số âm x Số dương = Số âm.
Hướng dẫn giải
Câu a
\((-5) . 6 = \,– (|–5| . |6|)\)\(= - (5.6) = -30\)
Câu b
\(9 . (-3) = – (|9| . |–3|)\)\(= - (9.3) = -27\)
Câu c
\((-10) . 11 = – (|–10| . |11|)\)\( = - (10. 11) = -110\)
Câu d
\(150 . (-4) = \,– ( |150| . |–4|)\)\(= - (150.4) = -600 \)
2. Giải bài 74 trang 89 SGK Toán 6 tập 1
Thực hiện phép tính:
a) \((-5) . 6\); b) \(9 . (-3)\);
c) \((-10) . 11\); d) \(150 . (-4)\)
Phương pháp giải
Quy tắc nhân hai số nguyên khác dấu: Muốn nhân hai số nguyên khác dấu, ta nhân hai giá trị tuyệt đối của chúng rồi đặt dấu " -" trước kết quả nhận được.
Hãy nhớ: Số âm x Số dương = Số âm.
Hướng dẫn giải
Câu a
\((-5) . 6 = \,– (|–5| . |6|)\)\(= - (5.6) = -30\)
Câu b
\(9 . (-3) = – (|9| . |–3|)\)\(= - (9.3) = -27\)
Câu c
\((-10) . 11 = – (|–10| . |11|)\)\( = - (10. 11) = -110\)
Câu d
\(150 . (-4) = \,– ( |150| . |–4|)\)\(= - (150.4) = -600 \)
3. Giải bài 75 trang 89 SGK Toán 6 tập 1
So sánh:
a) \( (-67) . 8 \) với \( 0\);
b) \( 15 . (-3)\) với \( 15 \);
c) \( (-7) . 2 \) với \( -7 \).
Phương pháp giải
Quy tắc nhân hai số nguyên khác dấu: Muốn nhân hai số nguyên khác dấu, ta nhân hai giá trị tuyệt đối của chúng rồi đặt dấu " -" trước kết quả nhận được.
Hãy nhớ: Số âm x Số dương = Số âm.
Hướng dẫn giải
Câu a
\( (-67) . 8 < 0\);
Vì tích của số âm và số dương là một số âm nên \( (-67) . 8 < 0\)
Cách khác:
\((–67) . 8 = – (67 . 8) = –536 < 0\)
Câu b
\( 15 . (-3) < 15\) (vì số dương nhân số âm kết quả là một số âm nên \(15 . (-3) < 0 < 15\))
Cách khác:
\(15 .(–3) = –(15 . 3) = –45 < 15\) (số nguyên âm luôn nhỏ hơn số nguyên dương).
Câu c
\( (-7) . 2 < -7\) (vì \( (-7) . 2 = -14<-7\)).
4. Giải bài 76 trang 89 SGK Toán 6 tập 1
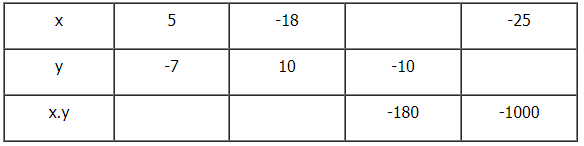
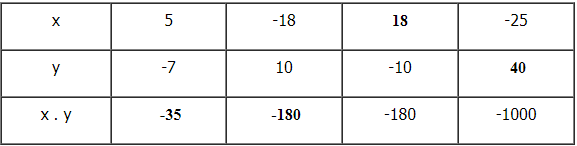
Điền vào ô trống:
Phương pháp giải
Quy tắc nhân hai số nguyên khác dấu: Muốn nhân hai số nguyên khác dấu, ta nhân hai giá trị tuyệt đối của chúng rồi đặt dấu " -" trước kết quả nhận được.
Chú ý: Số âm x Số dương = Số âm.
Hướng dẫn giải
Ta có bảng sau:
Giải thích:
+ \(x = 5, y = –7\) thì \(x . y = 5. ( –7) = – (5 . 7) = –35.\)
+ \(x = –18, y = 10\) thì \(x . y = (–18) . 10\)\( = – (18 . 10) = –180.\)
+ \(y = –10 ;\)\(x.y = x . (–10) = – (x.10) = – 180,\) do đó \(x . 10 = 180\) nên \(x =180:10= 18.\)
+\( x = –25; x.y = (–25).y = –(25.y) = –1000,\) do đó \(25.y = 1000\) nên \(y = 1000:25=40.\)
5. Giải bài 77 trang 89 SGK Toán 6 tập 1
Một xí nghiệp may mỗi ngày được 250 bộ quần áo. Khi may theo mốt mới, chiều dài của vải dùng để may một bộ quần áo tăng x dm (khổ vải như cũ). Hỏi chiều dài của vải dùng để may 250 bộ quần áo mỗi ngày tăng bao nhiêu đềximét, biết:
a) x = 3 ? b) x = -2 ?
Phương pháp giải
Tính chiều dài của vải để may \(250\) bộ quần áo sẽ tăng theo x nếu mỗi bộ tăng \(x\) dm
Từ đó thay \(x=3; x=-2\) rồi thực hiện phép tính nhân để có đáp án.
Hướng dẫn giải
Theo bài, chiều dài của vải để may 1 bộ quần áo tăng x (dm).
Suy ra, chiều dài của vải để may \(250\) bộ quần áo sẽ tăng \(250.x\) (dm).
Câu a
Với \(x = 3\) thì chiều dài vải tăng: \(250.3 = 750\) (dm)
Câu b
Với \(x = -2\) thì chiều dài vải tăng: \(250.(-2) =-(250.2)= -500\) (dm) tức là giảm 500 (dm)
Tham khảo thêm
- doc Giải bài tập SGK Toán 6 Bài 1: Làm quen với số nguyên âm
- doc Giải bài tập SGK Toán 6 Bài 2: Tập hợp các số nguyên
- doc Giải bài tập SGK Toán 6 Bài 3: Thứ tự trong tập hợp các số nguyên
- doc Giải bài tập SGK Toán 6 Bài 4: Cộng hai số nguyên cùng dấu
- doc Giải bài tập SGK Toán 6 Bài 5: Cộng hai số nguyên khác dấu
- doc Giải bài tập SGK Toán 6 Bài 6: Tính chất của phép cộng các số nguyên
- doc Giải bài tập SGK Toán 6 Bài 7: Phép trừ hai số nguyên
- doc Giải bài tập SGK Toán 6 Bài 8: Quy tắc dấu ngoặc
- doc Giải bài tập SGK Toán 6 Bài 9: Quy tắc chuyển vế
- doc Giải bài tập SGK Toán 6 Bài 11: Nhân hai số nguyên cùng dấu
- doc Giải bài tập SGK Toán 6 Bài 12: Tính chất của phép nhân
- doc Giải bài tập SGK Toán 6 Bài 13: Bội và ước của một số nguyên
- doc Giải bài tập SGK Toán 6 Ôn tập chương 2: Số nguyên