Toán 8 Chương 3 Bài 6: Trường hợp đồng dạng thứ hai

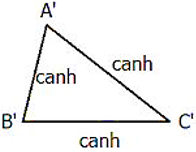
Nếu hai cạnh tam giác này tỉ lệ với hai cạnh của tam giác kia và góc tạo bởi các cặp cạnh đó bằng nhau, thì hai tam giác đồng dạng.

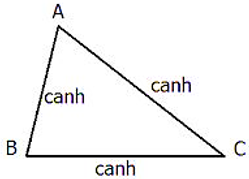
Tổng quát: Δ ABC,Δ A'B'C' có A'B'/AB = A'C'/AC = B'C'/BC ⇒ Δ ABC ∼ Δ A'B'C'

Ví dụ 1

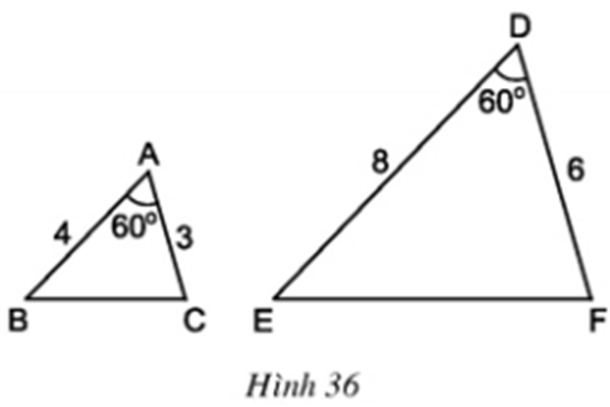
Cho hai tam giác $ABC$ và $DEF$ có kích thước như trong hình 36.

- So sánh các tỉ số $\dfrac{{AB}}{{DE}}$ và $\dfrac{{AC}}{{DF}}$

- Đo các đoạn thẳng $BC, EF$. Tính tỉ số $\dfrac{{BC}}{{EF}}$, so sánh với các tỉ số trên và dự đoán sự đồng dạng của hai tam giác $ABC$ và $DEF.$

Hướng dẫn giải

$\dfrac{{AB}}{{DE}} = \dfrac{{AC}}{{DF}} = \dfrac{1}{2}$

Đo các cạnh ta có: $BC \approx \,3,6 ; EF \approx 7,2$

$\eqalign{&  \Rightarrow {{BC} \over {EF}} = {1 \over 2}  \cr &  \Rightarrow {{AB} \over {DE}} = {{AC} \over {DF}} = {{BC} \over {EF}} = {1 \over 2} \cr}$

Dự đoán : $ΔABC$ đồng dạng $ΔDEF$. 

Ví dụ 2

Hãy chỉ ra các cặp tam giác đồng dạng với nhau từ các tam giác sau đây (h.38):

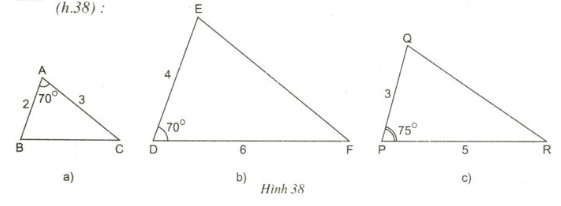
Hướng dẫn giải

Xét $ΔABC$ và $ΔDEF$ có:

$\eqalign{& \widehat A = \widehat D = {70^o}  \cr & {{AB} \over {AC}} = {{DE} \over {DF}} = {2 \over 3} \cr}$

$⇒ ΔABC$ đồng dạng $ΔDEF$ (c.g.c)

Ví dụ 3

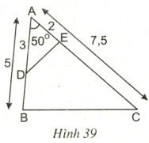
a) Vẽ tam giác $ABC$ có $\widehat {BAC} = {50^o}$, $AB = 5cm, AC = 7,5cm$ (h.39)

b) Lấy trên các cạnh $AB, AC$ lần lượt hai điểm $D, E$ sao cho $AD = 3cm, AE = 2cm$. Hai tam giác $AED$ và $ABC$ có đồng dạng với nhau không ? Vì sao ?

Hướng dẫn giải

a) Học sinh tự vẽ hình 

b) Ta có: $\dfrac{{AB}}{{AC}} = \dfrac{5}{{7,5}} = \dfrac{2}{3}$

$\dfrac{{AE}}{{AD}} = \dfrac{2}{3}$

Xét $\Delta ABC$ và $\Delta AED$ có

$\widehat A$ chung 

$\dfrac{{AB}}{{AC}} = \dfrac{{AE}}{{AD}} = \dfrac{2}{3}$

$\Rightarrow \Delta ABC$ đồng dạng $\Delta AED\,\,\left( {c.g.c} \right)$

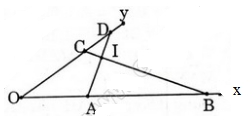
Trên một cạnh của góc $xOy$ ($\widehat {xOy} \ne {180^0}$), Đặt các đoạn thẳng $OA= 5cm, OB= 16cm$. Trên cạnh thứ hai của góc đó, đặt các đoạn $OC= 8cm, OD= 10cm$.

a) Chứng minh hai tam giác $OCB$ và $OAD$ đồng dạng.

b) Gọi giao điểm của các cạnh $AD$ và $BC$ là $I$, chứng minh rằng hai tam giác $IAB$ và $ICD$ có các góc bằng nhau từng đôi một.

Hướng dẫn giải

a) Ta có:

$\dfrac{OA}{OC} = \dfrac{5}{8}$ ; $\dfrac{OD}{OB} = \dfrac{10}{16} = \dfrac{5}{8}$ 

 $\Rightarrow \dfrac{OA}{OC} = \dfrac{OD}{OB}$

Xét  $∆OCB$ và $∆OAD$ có:

+) $\widehat O$ chung

+) $\dfrac{OA}{OC} = \dfrac{OD}{OB}$ (chứng minh trên)

 $\Rightarrow ∆OCB$ đồng dạng $∆OAD$ ( c-g-c)

$\Rightarrow \widehat {ODA} = \widehat {CBO}$ (2 góc tương ứng) hay $\widehat{CDI}$ = $\widehat{IBA}$ 

b) Xét $∆ICD$ và $∆IAB$ có

 $\widehat{CID}$ = $\widehat{AIB}$ (hai góc đối đỉnh)   (1)

$\widehat{CDI}$ = $\widehat{IBA}$ (theo câu a)            (2)

Theo định lí tổng ba góc trong một tam giác ta có:

$\eqalign{ & \widehat {CID} + \widehat {CDI} + \widehat {ICD} = {180^0} \cr & \widehat {AIB}+\widehat {IBA} + \widehat {IAB} = {180^0} \cr}$

$\Rightarrow \widehat {CID} + \widehat {CDI} + \widehat {ICD}$ $= \widehat {AIB}+\widehat {IBA} + \widehat {IAB}$   (3)

Từ (1), (2) và (3) suy ra: $\widehat {ICD}=\widehat {IAB}$

Vậy hai tam giác $IAB$ và $ICD$ có các góc bằng nhau từng đôi một. 

Chứng minh rằng nếu tam giác $A'B'C'$ đồng dạng với tam giác $ABC$ theo tỉ số $k$, thì tỉ số của hai đường trung tuyến tương ứng với hai tam giác đó cũng bằng $k$.

Hướng dẫn giải

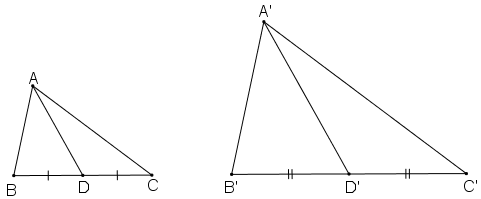
Giả sử $∆A'B'C'$ đồng dạng $∆ABC$ theo tỉ số $k, A'M', AM$ là hai đường trung tuyến tương ứng.

Vì $∆A'B'C'$ đồng dạng $∆ABC$ (giả thiết)

$\dfrac{A'B'}{AB} = \dfrac{B'C'}{BC}$ (tính chất hai tam giác đồng dạng)

Mà $B'C' = 2B'M', BC = 2BM$ (tính chất trung tuyến)

$\Rightarrow \dfrac{{A'B'}}{{AB}} = \dfrac{{2B'M'}}{{2BM}} = \dfrac{{B'M'}}{{BM}}$

Xét  $∆ABM$ và $∆A'B'M'$ có:

 $\widehat{B} = \widehat{B'}$ (vì $∆A'B'C'$ đồng dạng $∆ABC$) 

 $\dfrac{{A'B'}}{{AB}} = \dfrac{{B'M'}}{{BM}}$ (chứng minh trên)

$\Rightarrow ∆A'B'M'$ đồng dạng $∆ABM$ (c-g-c)

$\Rightarrow \dfrac{A'M'}{AM}= \dfrac{A'B'}{AB} = k.$

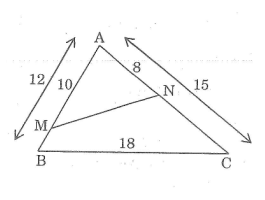
Câu 1: Cho tam giác $ABC$ có $AB = 12cm, AC = 15cm,$ $BC = 18cm.$

Trên cạnh $AB$, đặt đoạn thẳng $AM = 10cm,$ trên cạnh $AC$ đặt đoạn thẳng $AN = 8cm.$ Tính độ dài đoạn thẳng $MN.$

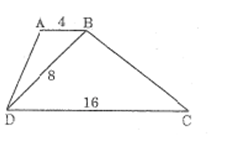
Câu 2: Hình thang $ABCD \;(AB // CD)$ có $AB = 4cm, CD = 16cm$ và $BD = 8cm$ (h23).

Chứng minh $\widehat {BAD} = \widehat {DBC}$ và $BC = 2 AD.$ 

Câu 3: Cho tam giác $ABC$ có $\widehat A = 60^\circ$, $AB = 6cm, AC = 9cm$

a) Dựng tam giác đồng dạng với tam giác $ABC$ theo tỉ số đồng dạng $\displaystyle k = {1 \over 3}$

b) Hãy nêu một vài cách dựng khác và vẽ hình trong từng trường hợp cụ thể.

Câu 4: Dựng tam giác $ABC$, biết $\widehat{A}={60^o}$ và, tỉ số $\dfrac{AB}{AC} = \dfrac{4}{5}$ và đường cao $AH = 6cm$.

Câu 1: Nếu hai tam giác MNP và QRS có $\frac{MN}{QS}=\frac{MP}{RS}$ và $\widehat{M}=\widehat{S}$ thì:

A. $\Delta MNP \sim \Delta QSR$

B. $\Delta MNP \sim \Delta SQR$

C. $\Delta MNP \sim \Delta RSQ$

D. $\Delta MNP \sim \Delta RSQ$

Câu 2: Nếu hai tam giác EFH và GKL có $\frac{EF}{GK}=\frac{EH}{GL}$ và $\widehat{E}=\widehat{G}$ thì:

A. $\widehat{EHF}=\widehat{GKL}$

B. $\widehat{ÈFH}=\widehat{GLK}$

C. $\widehat{FEH}=\widehat{LKG}$

D. $\widehat{EHF}=\widehat{KLG}$

Câu 3: Cho tam giác ABC, AAD là đường phân giác.Chứng minh được: 

A. $AD^{2}=AB.AC+DB.DC$

B. $AD^{2}=BD.DC-AB.AC$

C. $AD^{2}=AB.AC-DB.DC$

D. Cả a,b,c đều sai 

Câu 4: Cho hai tam giác ABC, DEF có AB=4cm, AC=6cm, BC=5cm, DE=2cm,EF=1cm, $\widehat{ABC}=\widehat{DEF}$.Chứng minh được:

A. $\widehat{BAC}=2\widehat{EDF}$

B. $\widehat{DFE}=\frac{\widehat{BAC}}{2}+\widehat{ACB}$

C.Cả a,b đều đúng 

D.Cả a,b đều sai 

Câu 5: Cho $\Delta MNP \sim \Delta EFH$ theo tỉ số k, MM', EE' lần lượt là hai trung tuyến của tam giác MNP và EFH. Ta chứng minh được.

A. $\frac{EE'}{MM'}=k$

B. $\frac{MM'}{EE'}=k^{2}$

C. $\frac{MM'}{EE'}=k$

D. $\frac{EE'}{MM'}=k^{2}$

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Nắm chắc nội dung định lý (GT, KL), hiểu được cách chứng minh gồm 2 bước chính.
• Vận dụng định lý để nhận biết được các cặp tam giác đồng dạng, làm các bài tập tính độ dài các cạnh và các bài tập chứng minh.