Toán 8 Chương 3 Bài 3: Tính chất đường phân giác của tam giác

* Đường phân giác trong của một tam giác chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn ấy.

* Đường phân giác ngoài tại một đỉnh của tam giác chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn thẳng ấy.

\(\begin{array}{l}\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\\\frac{{EB}}{{EC}} = \frac{{AB}}{{AC}}\end{array}\)                  

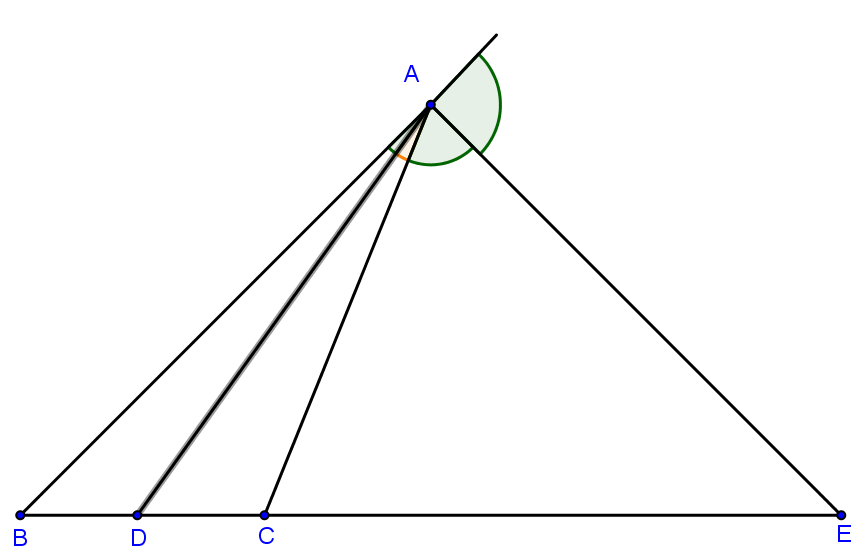
Như vậy, chân các đường phân giác trong và phân giác ngoài của một góc tại một đỉnh của tam giác là các điểm chia trong và chia ngoài cạnh đối diện theo tỉ số bằng tỉ số của hai cạnh bên tương ứng.

\(\frac{{DB}}{{DC}} = \frac{{EB}}{{EC}} = \frac{{AB}}{{AC}}.\)

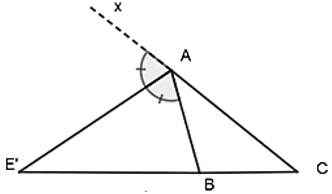
Định lí vẫn đúng với đường phân giác của góc ngoài của tam giác

AE' là phân giác của góc BAx ( AB ≠ AC )

Ta có: \(\frac{{AB}}{{AC}} = \frac{{E'B}}{{E'C}}\) hay \(\frac{{E'B}}{{AB}} = \frac{{E'C}}{{AC}}\)

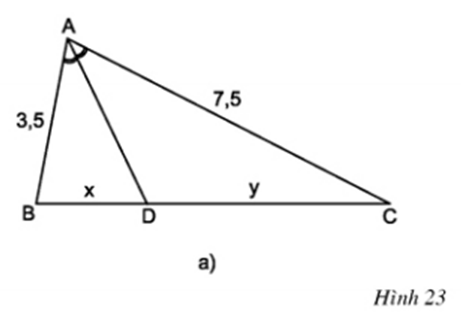
Xem hình 23a.

a) Tính \(\dfrac{x}{y}\)

b) Tính \(x\) khi \(y = 5\)

Hướng dẫn giải

a) Áp dụng tính chất đường phân giác của tam giác vào \(\Delta ABC\), phân giác \(AD\) ta có:

\(\eqalign{
& {{AB} \over {AC}} = {{BD} \over {DC}} \cr 
& \Rightarrow {{3,5} \over {7,5}} = {x \over y} \Rightarrow {x \over y} = {7 \over {15}} \cr} \)

b) Khi \(y = 5\)

\(\Rightarrow x = 5.\dfrac{7}{{15}} = \dfrac{7}{3}\)

Tính \(x\) trong hình 24 và làm tròn kết quả đến chữ số thập phân thứ nhất.

a) 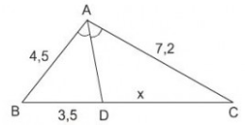  b) 

Hướng dẫn giải

a) \(AD\) là tia phân giác góc \(A\) của \(∆ABC\) (gt) nên áp dụng tính chất của đường phân giác trong tam giác ta có:

 \(\dfrac{BD}{AB} = \dfrac{DC}{AC}\)

\(\Rightarrow DC = \dfrac{BD.AC}{AB}= \dfrac{3,5.7,2}{4,5}\)

\(\Rightarrow x = 5,6\)

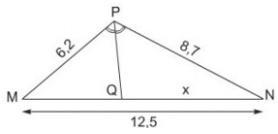
b) \(PQ\) là đường phân giác góc \(P\) của \(∆PMN\) (gt) nên 

\(\dfrac{MQ}{MP}= \dfrac{NQ}{NP}\) (tính chất đường phân giác của tam giác)

Hay  \(\dfrac{MQ}{6,2} = \dfrac{x}{8,7}\)

Có: \(MN=MQ+x=12,5\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\Rightarrow \dfrac{x}{8,7} = \dfrac{MQ}{6,2} = \dfrac{x + MQ}{8,7+ 6,2}= \dfrac{12,5}{14,9}\)

\( \Rightarrow x = \dfrac{{12,5.8,7}}{{14,9}} \approx 7,3\)

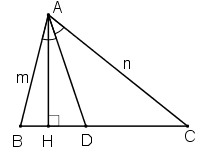
Tam giác \(ABC\) có độ dài các cạnh \(AB= m, AC= n\) và \(AD\) là đường phân giác. Chứng minh rẳng tỉ số diện tích tam giác \(ABD\) và diện tích tam giác \(ACD\) bằng \(\dfrac{m}{n}\).

Hướng dẫn giải

Kẻ \(AH ⊥ BC\) 

Ta có: 

\({S_{ABD}} = \dfrac{1}{2}AH.BD\)

\({S_{ACD}} = \dfrac{1}{2}AH.DC\)

\( \Rightarrow \dfrac{S_{ABD}}{S_{ACD}} = \dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.DC} = \dfrac{BD}{DC}\)

Mặt khác: \(AD\) là đường phân giác của \(∆ABC\) (gt)

\( \Rightarrow \dfrac{BD}{DC}= \dfrac{AB}{AC} = \dfrac{m}{n}\) (tính chất đường phân giác của tam giác)

Vậy \(\dfrac{S_{ABD}}{S_{ACD}} = \dfrac{m}{n}\) (điều phải chứng minh).

Câu 1: Tam giác \(ABC\) có \(AB = 15cm, AC = 20cm,\) \( BC = 25cm.\) Đường phân giác góc \(BAC\) cắt cạnh \(BC\) tại \(D\) (h.14)

a) Tính độ dài đoạn thẳng \(DB\) và \(DC\).

b) Tính tỉ số diện tích của hai tam giác \(ABD\) và \(ACD.\)

Câu 2: Tam giác \(ABC\) có các đường phân giác \(AD, BE\) và \(CF\) (h15).

Chứng minh rằng:

\(\displaystyle {{DB} \over {DC}}.{{EC} \over {EA}}.{{FA} \over {FB}} = 1\)

Câu 3: Tam giác cân \(BAC\) có \(BA = BC = a, AC = b.\) Đường phân giác góc \(A\) cắt \(BC\) tại \(M\), đường phân giác góc \(C\) cắt \(BA\) tại \(N\) (h16).

a) Chứng minh rằng: \(MN // AC.\) 

b) Tính \(MN\) theo \(a, b\).

Câu 4: Tam giác \(ABC\) có \(AB = 12cm, AC = 20cm,\) \(BC = 28cm.\) Đường phân giác góc \(A\) cắt \(BC\) tại \(D.\) Qua \(D\) kẻ \(DE // AB\) (\(E\) thuộc \(AC\)) (h17).

a) Tính độ dài đoạn thẳng \(BD, DC\) và \(DE\).

b) Cho biết diện tích tam giác \(ABC\) là \(S\), tính diện tích các tam giác \(ABD, ADE\) và \(DCE.\)

Câu 1: Cho tam giác ABC.Tia phân giác trong của góc A cắt BC tại D.Cho AB=6, AC=x,BD=9, BC=21.Hãy chọn kết quả đúng về độ dài x:

A. x=14

B. x=12

C. x=8

D. Một kết quả khác 

Câu 2: Cho tam giác ABC có AD là phân giác ngoài của góc A.D thuộc đường thẳng BC.Các dữ kiện được cho trên hình.Số đo nào sau đây là độ dài của đoạn CD

A. DC=10

B. DC=15

C. DC=6

D. DC=8

Câu 3: Tam giác ABC có cạnh AB=15cm, AC=20cm, BC=25cm.Đường phân giác góc BAC cắt cạnh BC tại D.Vậy độ dài DB là:

A. 10

B. \(10\frac{5}{7}\)

C. 14

D. \(14\frac{2}{7}\)

Câu 4: Tam giác ABC có AB=15cm,AC=20cm,BC=25cm.Đường phân giác góc BAC cắt BC tại D.Vậy tỉ số diện tích của hai tam giác ABD và ACD là:

A. \(\frac{1}{4}\)

B. \(\frac{1}{2}\)                               

C. \(\frac{3}{4}\)

D. \(\frac{1}{3}\)

Câu 5: Độ dài các cạnh tam giác BAC tỉ lệ với 2:3:4.BD là phân giác trong ứng với cạnh ngắn nhất AC,Chia AC thành hai đoạn AD và CD.Nếu độ dài AC là 10, thế thì độ dài của đoạn thẳng dài hơn trong hai đoạn AD và CD là:

A.3,5

B.5

C. \(\frac{40}{7}\)

D.6

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Biết được tính chất đường phân giác của tam giác
• Vận dụng tính chất đường phân giác trong tam giác để:
• Tính độ dài của đoạn thẳng
• Lập dãy tỉ số đoạn thẳng bằng nhau