Toán 8 Chương 3 Bài 5: Trường hợp đồng dạng thứ nhất

* Định lí: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng

$\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CA}}{{C'A'}} \Rightarrow \Delta ABC \sim \Delta A'B'C'$

Trường hợp đồng dạng này được ghi tóm tắt (c.c.c)

Ví dụ 1

Tam giác ABC vuông tại A có AB = 6cm, AC = 8cm và tam giác A'B'C' vuông tại A' có A'B'= 9cm, B'C' = 15cm. Hỏi hai tam giác vuông ABC và A'B'C' có đồng dạng với nhau không?

Hướng dẫn giải:

Áp dụng định lí pitago tính được cạnh huyền BC = 10cm và cạnh góc vuông A'C' = 12cm. từ đó ta có:

$\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CA}}{{C'A'}}\,\,\left( { = \frac{2}{3}} \right)$

Vậy tam giác ABC đồng dạng với tam giác A'B'C'

Ví dụ 2

Hai tam giác mà các cạnh có độ dài như sau có đồng dạng không?

a) 4cm, 5cm, 6cm và 8mm, 10mm, 12mm

b) 3cm, 4cm, 6cm và 9cm, 15cm, 18cm

Hướng dẫn giải:

a) Hai tam giác đồng dạng với nhau vì $\frac{{40}}{8} = \frac{{50}}{{10}} = \frac{{60}}{{12}}\,\,\left( { = 5} \right)$

b) Hai tam giác không đồng dạng với nhau vì $\frac{3}{9} \ne \frac{4}{{15}}$

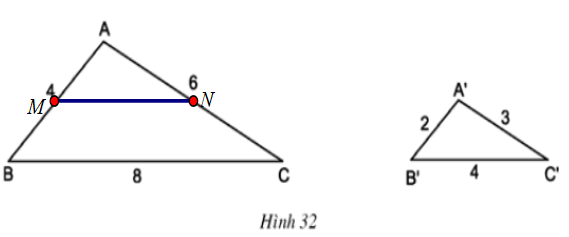
Hai tam giác $ABC$ và $A’B’C’$ có kích thước như trong hình 32 (có cùng đơn vị đo là xentimet)

Trên các cạnh $AB$ và $AC$ của tam giác $ABC$ lần lượt lấy hai điểm $M, N$ sao cho

$AM = A’B’ = 2cm; AN = A’C’ = 3cm$.

Tính độ dài đoạn thẳng $MN$.

Có nhận xét gì về mối quan hệ giữa các tam giác $ABC, AMN, A’B’C’$?

Hướng dẫn giải

$\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AC}} = \dfrac{1}{2}$

$⇒ MN // BC$ (định lí Ta lét đảo)

$\eqalign{&  \Rightarrow {{AM} \over {AB}} = {{AN} \over {AC}} = {{MN} \over {BC}} = {1 \over 2}  \cr &  \Rightarrow MN = {1 \over 2}BC = {1 \over 2}.8 = 4 \,cm\cr}$

Nhận xét:

$ΔAMN$ đồng dạng $ΔABC$ (vì MN//BC); $ΔAMN = ΔA’B’C'(c-c-c)$ nên $ΔAMN$ đồng dạng $ΔA’B’C'$

Từ đó: $ΔABC$ đồng dạng $ΔA’B’C’$ (cùng đồng dạng với $ΔAMN$)

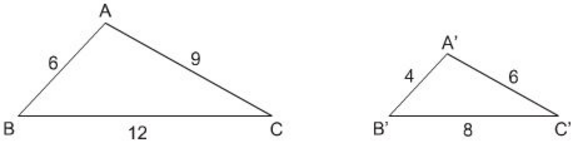
Cho tam giác $ABC$ và $A'B'C'$ có kích thước như trong hình 35.

a) Tam giác $ABC$ và $A'B'C'$ có đồng dạng với nhau không? Vì sao?

b) Tính tỉ số chu vi của hai tam giác đó.

Hướng dẫn giải

a) Ta có: 

$\begin{array}{l} \dfrac{{AB}}{{A'B'}} = \dfrac{6}{4} = \dfrac{3}{2};\,\,\dfrac{{AC}}{{A'C'}} = \dfrac{9}{6} = \dfrac{3}{2};\\\dfrac{{BC}}{{B'C'}} = \dfrac{{12}}{8} = \dfrac{3}{2}\\ \Rightarrow \dfrac{{AB}}{{A'B'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{3}{2} \end{array}$

$\Rightarrow \Delta ABC \text{ đồng dạng }\Delta A'B'C'$ $\left( c-c-c \right)$

b) Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\dfrac{{AB}}{{A'B'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{{BC}}{{B'C'}}$$\, = \dfrac{{AB + AC + BC}}{{A'B' + A'C' + B'C'}}$ $= \dfrac{{{C_{ABC}}}}{{{C_{A'B'C'}}}} = \dfrac{3}{2}$

(với $C_{ABC}$ và $C_{A'B'C'}$ lần lượt là chu vi của hai tam giác $ABC, A'B'C')$ 

Vậy tỉ số chu vi của tam giác ABC và chu vi của tam giác A’B’C’ là $\dfrac{3}{2}$  

Tam giác $ABC$ có độ dài các cạnh là $AB = 3cm, AC = 5cm, BC = 7cm$. Tam giác $A'B'C'$ đồng dạng với tam giác $ABC$ và có chu vi bằng $55 cm$. 

Hãy tính độ dài các cạnh của $A'B'C'$ (làm tròn đến chữ số thập phân thứ hai).

Hướng dẫn giải

$\Rightarrow \Delta ABC$ đồng dạng $\Delta A'B'C'\left( {gt} \right)$

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\dfrac{{AB}}{{A'B'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{{BC}}{{B'C'}}$$\, = \dfrac{{AB + AC + BC}}{{A'B' + A'C' + B'C'}}$ $= \dfrac{{{C_{ABC}}}}{{{C_{A'B'C'}}}}$

hay $\dfrac{3}{A'B'}$ = $\dfrac{7}{B'C'}$ = $\dfrac{5}{A'C'}$ = $\dfrac{C_{ABC}}{55}$ = $\dfrac{3 + 7 + 5}{55}$ = $\dfrac{{15}}{{55}}$ = $\dfrac{3}{11}$

(với $C_{ABC}$ và $C_{A'B'C'}$ lần lượt là chu vi của hai tam giác $ABC, A'B'C'$)  

$+ )\,\,\dfrac{3}{{A'B'}} = \dfrac{3}{{11}}$$\; \Rightarrow A'B' = \dfrac{{3.11}}{3} = 11\,cm$ 

$+ )\,\,\dfrac{7}{{B'C'}} = \dfrac{3}{{11}}$$\; \Rightarrow B'C' = \dfrac{{7.11}}{3} \approx  25,67\,cm$

$+ )\,\,\dfrac{5}{{A'C'}} = \dfrac{3}{{11}}$$\; \Rightarrow A'C' = \dfrac{{5.11}}{3} \approx 18,33\,cm$ 

Câu 1: Hai tam giác mà các cạnh có độ dài như sau có đồng dạng không?

a) $4cm, 5cm, 6cm$ và $8mm, 10mm, 12mm$;

b) $3cm, 4cm, 6cm$ và $9cm, 15cm, 18cm;$

c) $1dm, 2dm, 2dm$ và $1dm, 1dm, 0,5dm$.

Câu 2: Tam giác vuông $ABC$ ($\widehat A = 90^\circ$) có $AB = 6cm, AC = 8cm$ và tam giác vuông $A’B’C’$ ($\widehat {A'} = 90^\circ$) có $A’B’ = 9cm, B’C’ = 15cm.$

Hỏi rằng hai tam giác vuông $ABC$ và $A’B’C’$ có đồng dạng với nhau không? Vì sao?

Câu 3: Tam giác $ABC$ có ba đường trung tuyến cắt nhau tại $O.$ Gọi $P, Q, R$ thứ tự là trung điểm của các đoạn thẳng $OA, OB, OC.$

Chứng minh rằng tam giác $PQR$ đồng dạng với tam giác $ABC.$

Câu 4: Tam giác $ABC$ có ba góc nhọn và có trực tâm là điểm $H.$ Gọi $K, M, N$ thứ tự là trung điểm của các đoạn thẳng $AH, BH, CH.$

Chứng minh rằng tam giác $KMN$ đồng dạng với tam giác $ABC$ với tỉ số đồng dạng $\displaystyle k = {1 \over 2}$.

Câu 1: Chọn đáp án sai. Hai tam giác ABC và MNP có $\widehat{BAC}=\widehat{NMP}=90^{\circ}$, AB=3cm, BC=5cm, MN=6cm, MP=8cm thì chứng minh được:

A. $\Delta ABC\sim \Delta MNP$

B. $\widehat{ACB}=\widehat{MPN}$

C. Cả a, b đều sai 

D. Cả a,b đều đúng 

Câu 2: $\Delta ABC\sim \Delta EDC$, AB=3; AC=2; CD=3,5; DE=6; BC=x;CE=y. Tỉ số các độ dài x,y là:

A. 7

B. $\frac{7}{2}$

C. $\frac{7}{4}$

D. $\frac{7}{16}$

Câu 3: Cho tam giác ABC, AB=8; BC=7; CA=6.kéo dài cạnh BC một đoạn CP sao cho tam giác PAB đồng dạng với tam giác PCA.Độ dài cạnh PC là:

A. 7

B. 8

C. 9

D. 10

Câu 4: Những đường thẳng song song L và L' đi qau A và C , Vuông góc vỡi BD và chia đường chéo BD của hình chữ nhật ABCD thành ba đoạn có độ dài bằng 1.Diện tích hình chữ nhật làm tròn đến chữ số thập phân là:

A. 4,1

B. 4,2

C. 4,3

D. 4,4

Câu 5: Cho tam giác ABC. D,E lần lượt trên các cạnh AB,AC sao cho AD.AC=AE.AB. Chứng minh được

A. AD.CE=BD.AE

B. $\frac{BD}{AD}=\frac{CE}{AE}$

C. DE//BC

D. $\frac{AD}{BD}=\frac{CE}{AE}$

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Nắm vững nội dung định lí về trường hợp đồng dạng thứ nhất
• Biết vận dụng định lý để nhận biết các cặp tam giác đồng dạng