Toán 9 Ôn tập chương 3: Góc với đường tròn

Góc có đỉnh trùng với tâm của đường tròn được gọi là góc ở tâm.

Hai cạnh của góc ở tâm cắt đường tròn tại hai điểm, do đó chia đường tròn thành hai cung.

Với các góc α ( 0 < α < 180°) thì cung nằm bên trong góc được gọi là cung nhỏ.

Cung nằm bên ngoài góc được gọi là cung lớn.

Định nghĩa

Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

Cung nằm bên trong góc được gọi là cung bị chắn.

Định lí

Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.

Hệ quả

Trong một đường tròn:

Các góc nội tiếp bằng nhau chắn các cung bằng nhau

Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau

Góc nội tiếp (nhỏ hơn hoặc bằng 900) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung

Góc nội tiếp chắn nửa đường tròn là góc vuông

Khái niệm

Góc tạo bởi tiếp tuyến và dây cung là góc có đỉnh nằm trên đường tròn, hai cạnh của góc gồm một tia là tiếp tuyến với đường tròn, tia còn lại chứa dây cung.

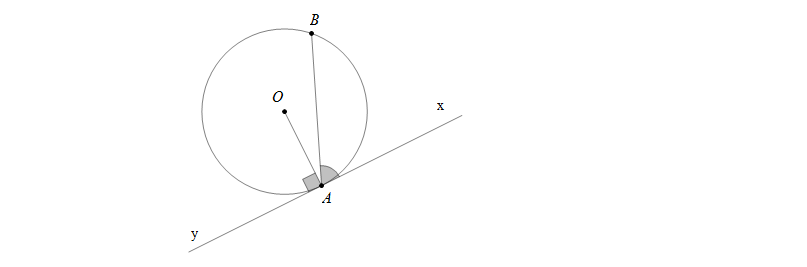
Góc $\widehat{BAx}$ (hoặc $\widehat{BAy}$) là góc tạo bởi tiếp tuyến và dây cung.

Định lí

Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.

ĐỊNH LÍ: Số đo của góc có đỉnh bên trong đường tròn bẳng nửa tổng số đo hai cung bị chắn.

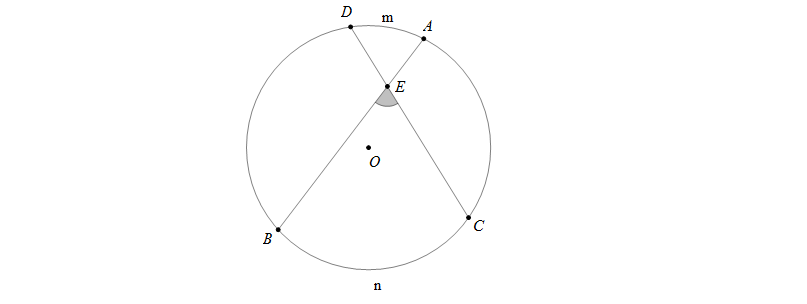
Góc $\widehat{BEC}$ là góc có đỉnh $E$ nằm bên trong đường tròn nên $\widehat{BEC}=\frac{1}{2}$(sđ$\stackrel\frown{BnC}$+sđ$\stackrel\frown{AmD}$)

ĐỊNH LÍ: Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

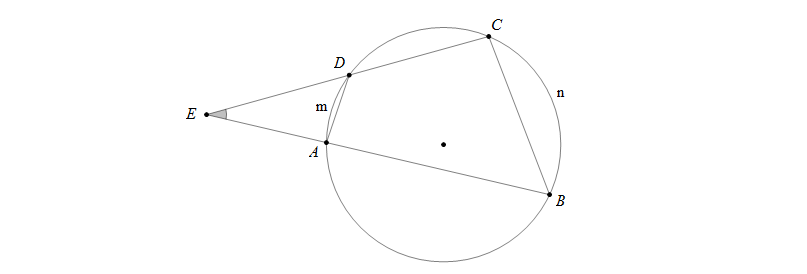
Góc $\widehat{AED}$ có đỉnh $E$ bên ngoài đường tròn nên $\widehat{AED}=\frac{1}{2}$(sđ$\stackrel\frown{BnC}-$sđ$\stackrel\frown{AmD}$)

Với đoạn thẳng $AB$ và góc $\alpha(0^0<\alpha<180^0)$ cho trước thì quỹ tích các điểm $M$ thỏa mãn $\widehat{AMB}=\alpha$ là hai cung chứa góc $\alpha$ dựng trên đoạn $AB$

Chú ý:

- Hai cung chứa góc $\alpha$ nói trên là hai cung đối xứng với nhau qua $AB$

- Hai điểm $A,B$ được coi là thuộc quỹ tích

- Trường hợp $\alpha=90^0$ thì quỹ tích trên là hai nửa đường tròn đường kính $AB$

Định nghĩa: Một tứ giác có bốn đỉnh cùng nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (hay tứ giác nội tiếp)

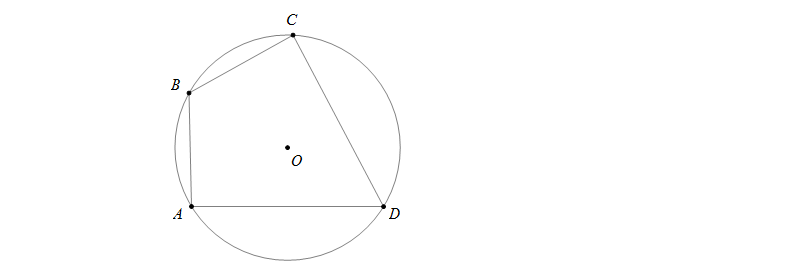
Chẳng hạn, tứ giác $ABCD$ có bốn đỉnh $A,B,C,D$ cùng nằm trên một đường tròn nên $ABCD$ được gọi là tứ giác nội tiếp.

Định lí: Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180⁰

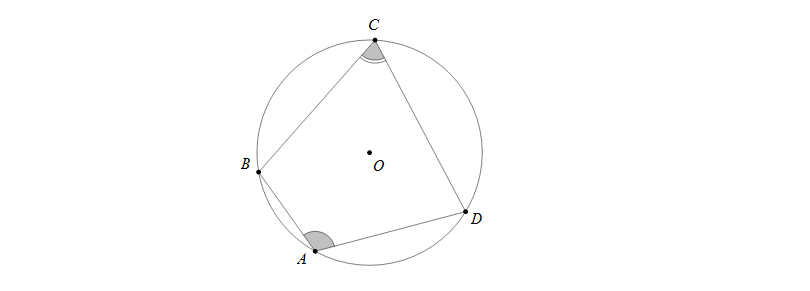
$ABCD$ là tứ giác nội tiếp nên ta có $\widehat{A}+\widehat{C}=\widehat{B}+\widehat{D}=180^0$

Định lí đảo: Nếu một tứ giác có tổng số đo hai góc đối nhau bằng 1800 thì tứ giác đó nội tiếp được đường tròn

Cụ thể ở hình trên, nếu có $\widehat{A}+\widehat{C}=180^0$ hoặc $\widehat{B}+\widehat{D}=180^0$ thì tứ giác $ABCD$ nội tiếp được đường tròn.

"Độ dài đường tròn" được kí hiệu là C, hay còn gọi là chu vi hình tròn được tính bằng công thức $C=2\pi R$ với $R$ là bán kính của đường tròn

Trên đường tròn bán kính $R$, độ dài $l$ cả một cung $n^0$ được tính theo công thức $l=\frac{\pi Rn}{180}$

$S=\frac{\pi R^2n}{360}$ hoặc $S=\frac{lR}{2}$

Cho đường tròn (O) có đường kính AB bằng 12cm. Một đường thẳng qua A cắt đường tròn (O) ở M và cắt tiếp tuyến của đường tròn tại B ở N. Gọi I là trung điểm của MN. Biết rằng AI=13cm,độ dài đoạn thẳng AM là:

Hướng dẫn giải

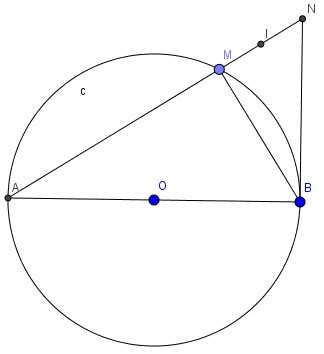
Đặt $AM=x, MI=NI=y$

Khi đó theo đề bài ta có $x+y=13$ (1) (AI=13cm)

Mặt khác áp dụng hệ thức lượng cho tam giác vuông ABN với đường cao BM ta có $AB^2=AM.AN$ hay $12^2=x(x+2y)$ (2)

Từ (1) ta có $y=13-x$ thế vào (2) ta được: $x(x+2(13-x))=12^2\Leftrightarrow -x^2+26x-144=0$

Dễ dàng giải phương trình trên bằng công thức nghiệm ta được $x=18 ,x=8$

Kết hợp với điều kiện ta suy ra AM=8cm

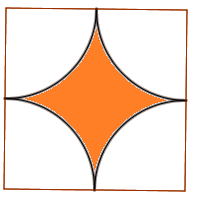
Cho viên gạch men được mô phỏng như hình, hãy tính diện tích bị tô màu, biết viên gạch hình vuông có cạnh là 40cm

Hướng dẫn giải

Ta có diện tích của viên gạch hình vuông là $S_{hv}=40.40=1600(cm^2)$

Bốn góc không tô màu chính là diện tích hình tròn có bán kính bằng 20cm.

Vậy, diện tích phần không tô màu là: $S_{ktm}=\pi r^2=20.20.\pi=400\pi(cm^2)$

Diện tích phần tô màu là: $S=1600-400\pi\approx 344(cm^2)$

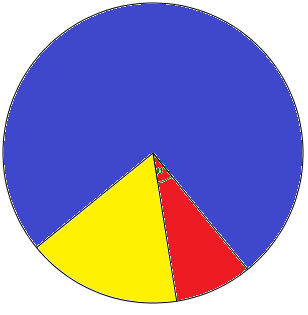
Đồ thị trên biểu diễn hình quạt phân phối học sinh của một trường thuộc vùng quê, trong đó, màu xanh hiển thị học sinh cấp 1, màu vàng hiển thị cấp 2 và màu đỏ hiển thị cấp 3.

biết rằng giá trị góc $\alpha=30^{\circ}$ và tổng học sinh cấp 2 và cấp 3 chỉ bằng $\frac{1}{4}$ học sinh cấp 1. Tổng số học sinh trong trường là 720 em. Tính số học sinh mỗi cấp.

Hướng dẫn giải

Ta thấy rằng số học sinh cấp 2 và 3 có tổng là $\frac{1}{4}$ nên số học sinh của hai cấp này là $\frac{720}{4}=180$ em.

Số học sinh cấp 1 của trường này là $720-180=540$ em

Vì góc $\alpha =30^{\circ}\Rightarrow$ số học sinh cấp 3 bằng $\frac{30}{90}=\frac{1}{3}$ số học sinh của cấp 2 và 3.

Số học sinh cấp 3 là: $\frac{180}{3}=60$ em.

Số học sinh cấp 1 là $180-60=120$ em

Cho đường tròn (O). Vẽ hai dây cung AC và BD bằng nhau và vuông góc với nhau tại điểm I (B thuộc cung nhỏ AC). Chứng minh rằng ABCD là hình thang cân.

Hướng dẫn giải

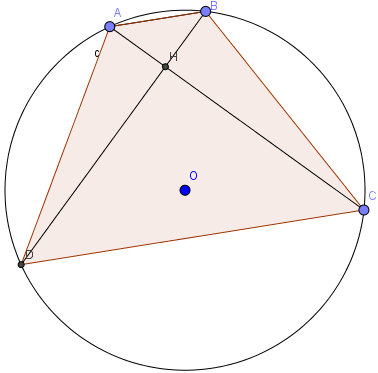
Gọi giao điểm của AC và BD là H

Ta có hai dây AC và BD bằng nhau và cùng vuông góc với nhau nên:

sđAD=sđBC.

Suy ra hai tam giác HCD và HAB đều vuông cân tại H

$\widehat{BDC}=\widehat{ABD}$

ABCD là hình thang.

Lưu ý: Hình thang nội tiếp đường tròn luôn là hình thang cân

Tam giác ABC đều nội tiếp đường tròn (O). M là điểm chính giữa cung nhỏ BC, AM cắt BC tại E. chứng minh $AB.BM=AM.BE$ 

Hướng dẫn giải

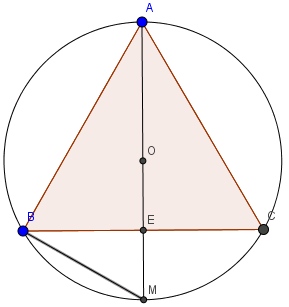
Ta có, M là điểm chính giữa cung BC nên $\widehat{BAM}=\widehat{CAM}$

Mặc khác tam giác ABC đều nên AM chính là đường trung trực của BC.

Và AM chính là đường kính của đường tròn (O)

$\Rightarrow \widehat{MBA}=90^o$

Dễ dàng chứng minh $\Delta ABM\sim \Delta BEM(g.g)$

Nên $\frac{AB}{BE}=\frac{AM}{BM}\Leftrightarrow AB.BM=AM.BE$

Câu 1: Cho đường tròn đường kính $AB.$ Qua $A$ và $B$ kẻ hai tiếp tuyến của đường tròn đó. Gọi $M$ là một điểm trên đường tròn. Các đường thẳng $AM$ và $BM$ cắt các tiếp tuyến trên lần lượt tại $B’$ và $A’.$

$a)$ Chứng minh rằng ${\rm{AA}}'.BB' = A{B^2}$

$b)$ Chứng minh rằng $A'{A^2} = A'M.A'B$

Câu 2: Cho lục giác $ABCDEF.$ Chứng minh rằng đường chéo $BF$ chia $AD$ thành hai đoạn thẳng theo tỉ số $1: 3.$

Câu 3: Cho tam giác $ABC$ có ba góc nhọn. Dựng điểm $M$ nằm trong tam giác $ABC$ sao cho $\widehat {AMB} = \widehat {BMC} = \widehat {CMA}$

Câu 4: Hai ròng rọc có tâm $O, O’$ và bán kính $R = 4a,$ $R’ = a.$ Hai tiếp tuyến chung $MN$ và $PQ$ cắt nhau tại $A$ theo góc $60^\circ.$ Tìm độ dài của dây cua- roa mắc qua hai ròng rọc.

Câu 1: Cho đường tròn đường kính AB và dây AC sao cho số đo cung AC là 60 độ. Số đo góc OCB là:

​A. $\widehat{OCB}=15^o$

B. $\widehat{OCB}=20^o$

C. $\widehat{OCB}=25^o$

D. $\widehat{OCB}=30^o$

Câu 2: Cho đường tròn (O;R). Vẽ dây AB sao cho số đo cung nhỏ AB bằng $\frac{1}{2}$ số đo cung lớn AB. Diện tích tam giác AOB là:

A. $\frac{R^2\sqrt{3}}{4}$

B. $\frac{R^2\sqrt{3}}{2}$

C. $R^2\sqrt{3}$

D. $2R^2\sqrt{3}$

Câu 3: Cho viên gạch men được mô phỏng như hình, diện tích bị tô màu là bao nhiêu? (biết viên gạch hình vuông có cạnh là 80cm)

A. $\approx 1373,45(cm^2)$

B. $\approx 1375,55(cm^2)$

C. $\approx 1385,55(cm^2)$

D. $\approx 1345,65(cm^2)$

Câu 4: Cho biết tam giác OBC đều, hai đoạn thẳng OB và CD tạo với nhau một góc bao nhiêu độ $(\leq 90^{\circ})$

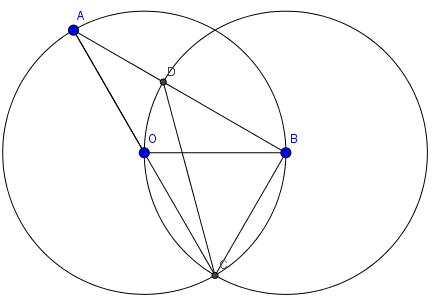
A. $65^o$

B. $75^o$

C. $105^o$

D. $115^o$

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Biết vận dụng các kiến thức vào việc giải bài tập về tính toán các đại lượng liên quan đến đường tròn , hình tròn.
• Phát biểu được các khái niệm, đọc, vẽ hình,.... Vận dụng giải các bài toán