Toán 9 Chương 3 Bài 10: Diện tích hình tròn, hình quạt tròn
Ở bài trước, chúng ta đã biết cách tính độ dài cung tròn, đường tròn. Nó thực chất là đường bao quanh cái đường tròn, thế còn phần trong đường tròn thì sao? Sau đây là bài Diện tích hình tròn, hình quạt tròn
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Công thức tính diện tích hình tròn
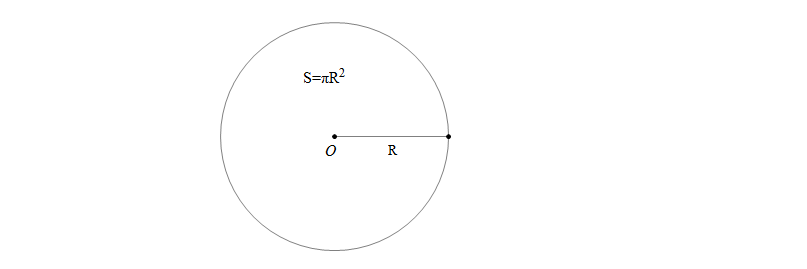
Diện tích hình tròn với bán kính R được tính theo công thức: \(S=\pi R^2\)
1.2. Công thức tính diện tích hình quạt tròn
Diện tích hình quạt tròn bán kính R, cung n0 được tính theo công thức
\(S=\frac{\pi R^2n}{180}\) hay \(S=\frac{l R}{2}\) (với \(l\) là độ dài cung n0 của hình quạt tròn)
2. Bài tập minh hoạ
2.1. Bài tập cơ bản
Câu 1: Tính diện tích hình tròn ngoại tiếp hình vuông có cạnh là 10cm
Hướng dẫn giải
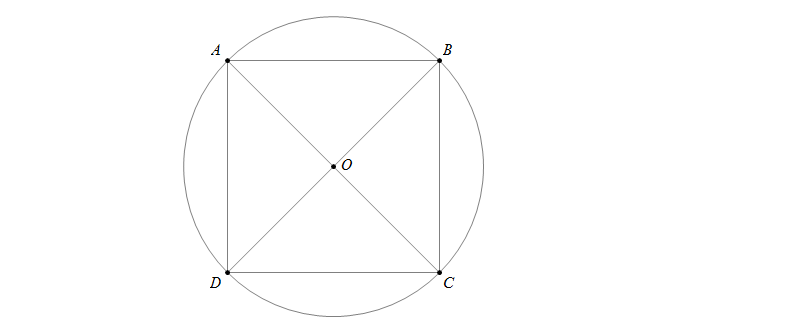
Ta đã biết bán kính đường tròn ngoại tiếp hình vuông ABCD là OA.
Cạnh hình vuông là 10cm nên AB=10cm
Áp dụng định lí Pytago cho tam giác vuông OAB ta có \(2OA^2=AB^2\Rightarrow2OA^2=10^2\Rightarrow OA=5\sqrt{2} (cm)\)
Diện tích hình tròn ngoại tiếp hình vuông là \(S=\pi R^2=\pi (5\sqrt{2})^2=50\pi (cm^2)\)
Câu 2: Tính diện tích hình quạt tròn có bán kính là 20cm, số đo cung là 300
Hướng dẫn giải
Áp dụng công thức tính diện tích hình quạt tròn, ta có
\(S=\frac{\pi R^2n}{360}=\frac{\pi.20^2.30}{360}=\frac{100\pi}{3} (cm^2)\)
Câu 3: Diện tích hình tròn sẽ thay đổi như thế nào nếu tăng bán kính lên gấp ba lần?
Hướng dẫn giải
Ta có \(S_1=\pi R^2\) với R là bán kính bao đầu
Sau khi tăng bán kính lên 3 lần thì bán kính hình tròn mới là 3R
Lúc đó, diện tích hình tròn là \(S_2=\pi (3R)^2=9\pi R^2\)
Vì \(\frac{S_2}{S_1}=\frac{9\pi R^2}{\pi R^2}=9\) nên diện tích hình tròn tăng lên 9 lần sau khi thay đổi bán kính
2.2. Bài tập nâng cao
Biết chu vi hình tròn là \(16\pi (cm)\). Tính diện tích hình quạt tròn có số đo cung là 500
Hướng dẫn giải
Chu vi hình tròn là \(16\pi (cm)\) nên \(C=2\pi R\Rightarrow R=\frac{16\pi}{2\pi}=8(cm)\)
Diện tích hình quạt tròn số đo cung 500 là \(S=\frac{\pi R^2n}{360}=\frac{\pi 8^2.50}{360}=\frac{80}{9}\pi (cm^2)\)
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: \(a)\) Điền vào ô trống trong bảng sau (\(S\) là diện tích hình tròn bán kính \(R\)).
|
\(R\) |
\(0\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(5\) |
\(10\) |
\(20\) |
|
\(S\) |
|
|
|
|
|
|
|
|
\(b)\) Vẽ đồ thị biểu diễn diện tích hình tròn theo bán kính của nó.
\(c)\) Diện tích hình tròn có tỉ lệ thuận với bán kính không?
Câu 2: \(a)\) Điền vào ô trống trong bảng sau (\(S\) là diện tích hình quạt \(n^\circ\)).
|
Cung \(n^\circ\) |
\(0\) |
\(45\) |
\(90\) |
\(180\) |
\(360\) |
|
\(S\) |
|
|
|
|
|
\(b)\) Vẽ đồ thị biểu diễn diện tích hình quạt theo \(n^\circ\).
\(c)\) Diện tích hình quạt có tỉ lệ thuận với số đo độ của cung không\(?\)
Câu 3: Cho đường trong \((O; R).\) Chia đường tròn này thành ba cung có số đo tỉ lệ với \(3, 4\) và \(5\) rồi tính diện tích các hình quạt tròn được tạo thành.
Câu 4: Cho tam giác \(ABC\) nội tiếp đường tròn \((O; R)\) có \(\widehat C = {45^\circ}\).
\(a)\) Tính diện tích hình quạt tròn \(AOB\) (ứng với cung nhỏ \(AB\))
\(b)\) Tính diện tích hình viên phân \(AmB\) (ứng với cung nhỏ \(AB\))
3.2. Bài tập trắc nghiệm
Câu 1: Tính diện tích hình quạt tròn có bán kính là 10cm và độ dài cung tròn là \(\frac{5}{2}\pi (cm)\)
A. \(50\pi (cm^2)\)
B. \(\frac{25}{3}\pi (cm^2)\)
C. \(\frac{25}{2}\pi (cm^2)\)
D. \(25\pi (cm^2)\)
Câu 2: Diện tích nửa hình tròn đường kính 4R bằng
A. \(R^2\pi\)
B. \(4R^2\pi\)
C. \(2R^2\pi\)
D. \(8R^2\pi\)
Câu 3: Diện tích hình tròn sẽ thay đổi như thế nào nếu tăng bán kính lên 2 lần?
A. Diện tích giảm 2 lần
B. Diện tích giảm 4 lần
C. Diện tích tăng 2 lần
D. Diện tích tăng 4 lần
Câu 4: Tính diện tích hình tròn biết chu vi của nó là \(10\pi (dm)\)
A. \(50\pi (dm^2)\)
B. \(25\pi (dm^2)\)
C. \(100\pi (dm^2)\)
D. \(64\pi (dm^2)\)
Câu 5: Một con bò bị nhốt trong một cái chuồng hình vuông có cạnh là 5m. Nhưng vì trong chuồng còn để nuôi heo, gà,... nên ông chủ phải buộc con bò ở một góc chuồng (cái cột ở góc chuồng), ông chủ đã dùng sợi dây thừng dài 1,5m để buộc con bò. Hỏi con bò có thể di chuyển trong mảnh đất có diện tích là bao nhiêu?
A. \(25\pi (m^2)\)
B. \(3\pi (m^2)\)
C. \(\frac{9}{16}\pi (m^2)\)
D. \(4,5\pi (m^2)\)
4. Kết luận
Qua bài học này, các em nắm được một số nội dung chính như sau:
- Phát biểu được công thức tính diện tích hình tròn, diện tích hình quạt tròn.
- Vận dụng được các công thức đã học vào giải một số bài toán thực tế.
Tham khảo thêm
- doc Toán 9 Chương 3 Bài 1: Góc ở tâm và số đo cung
- doc Toán 9 Chương 3 Bài 2: Liên hệ giữa cung và dây
- doc Toán 9 Chương 3 Bài 3: Góc nội tiếp
- doc Toán 9 Chương 3 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung
- doc Toán 9 Chương 3 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
- doc Toán 9 Chương 3 Bài 6: Cung chứa góc
- doc Toán 9 Chương 3 Bài 7: Tứ giác nội tiếp
- doc Toán 9 Chương 3 Bài 8: Đường tròn ngoại tiếp và đường tròn nội tiếp
- doc Toán 9 Chương 3 Bài 9: Độ dài đường tròn, cung tròn
- doc Toán 9 Ôn tập chương 3: Góc với đường tròn



