Toán 9 Chương 3 Bài 7: Tứ giác nội tiếp

Định nghĩa: Một tứ giác có bốn đỉnh cùng nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (hay tứ giác nội tiếp)

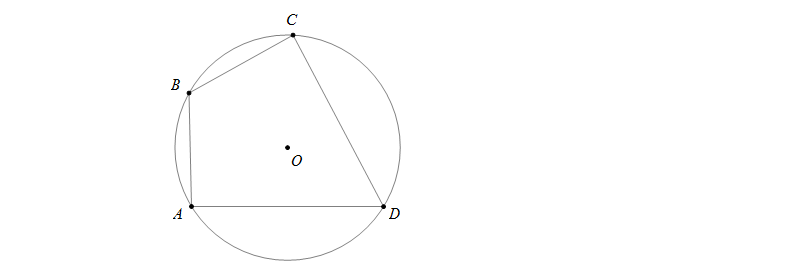
Chẳng hạn, tứ giác \(ABCD\) có bốn đỉnh \(A,B,C,D\) cùng nằm trên một đường tròn nên \(ABCD\) được gọi là tứ giác nội tiếp.

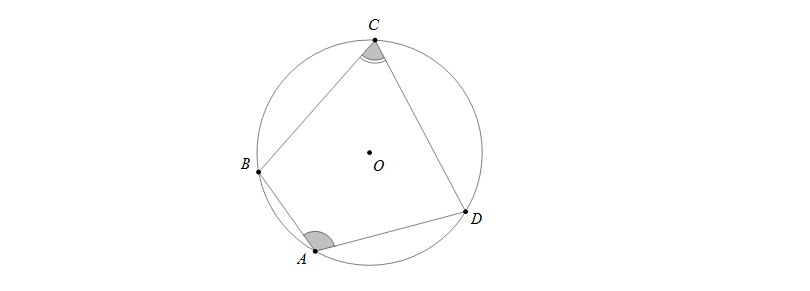
\(ABCD\) là tứ giác nội tiếp nên ta có \(\widehat{A}+\widehat{C}=\widehat{B}+\widehat{D}=180^0\)

Cụ thể ở hình trên, nếu có \(\widehat{A}+\widehat{C}=180^0\) hoặc \(\widehat{B}+\widehat{D}=180^0\) thì tứ giác \(ABCD\) nội tiếp được đường tròn.

- Tứ giác có tổng hai góc đối bằng \(180^\circ \). 

- Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó.

- Tứ giác có bốn đỉnh cách đều một điểm (mà có thể xác định được). Điểm đó là tâm đường tròn ngoại tiếp tứ giác.

- Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới cùng một góc \(\alpha \).

Câu 1: 

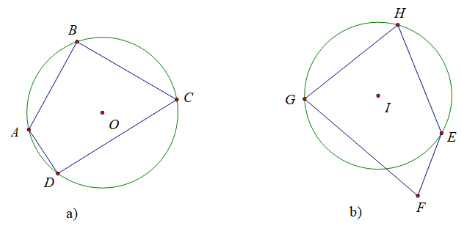
a) Vẽ một đường tròn tâm O rồi vẽ một tứ giác có tất cả các đỉnh nằm trên đường tròn đó.

b) Vẽ một đường tròn tâm I rồi vẽ một tứ giác có ba đỉnh nằm trên đường tròn đó còn đỉnh thức tư thì không.

Hướng dẫn giải

Câu 2: Tính số đo các góc của tứ giác \(ABCD\), biết rằng \(\widehat{DCx}=130^0\)

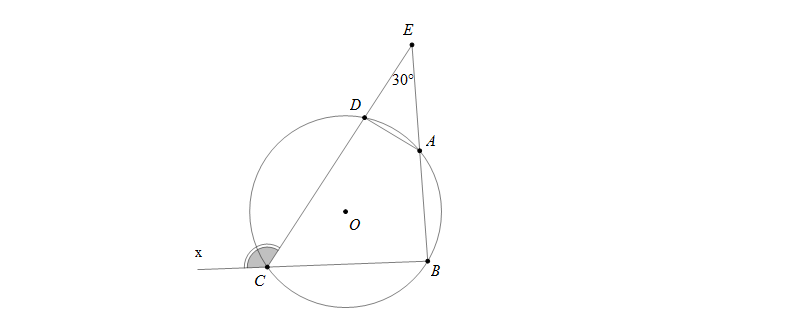
Hướng dẫn giải

Ta có \(\widehat{DCB}=180^0-\widehat{DCx}=180^0-130^0=50^0\), suy ra \(\widehat{DAB}=180^0-\widehat{DCB}=180^0-50^0=130^0\)

Lại có \(\widehat{DCx}\) là góc ngoài của \(\bigtriangleup ECB\) nên \(\widehat{DCx}=\widehat{E}+\widehat{B}\Rightarrow \widehat{B}=\widehat{DCx}-\widehat{E}=130^0-30^0=100^0\)

Từ đó suy ra \(\widehat{ADC}=180^0-\widehat{ABC}=180^0-100^0=80^0\)

Câu 1: Xem hình 45. Hãy chứng minh định lý trên.

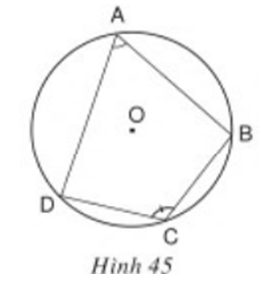
Hướng dẫn giải

Xét đường tròn \((O)\) ta có:

\(\widehat {BAD} = \dfrac{1}{2}sđ\,\overparen {BCD}\) (góc nội tiếp chắn cung \(BCD\))

\(\widehat {BCD} = \dfrac{1}{2}sđ\,\overparen {BAD}\) (góc nội tiếp chắn cung \(BAD\))

Suy ra \(\widehat {BAD} + \widehat {BCD} = \dfrac{1}{2}sđ\,\overparen {BCD} + \dfrac{1}{2}sđ\,\overparen {BAD} = \dfrac{{sđ\,\overparen {BAD} + sđ\,\overparen {BCD}}}{2}\) \( = \dfrac{{360^\circ }}{2} = 180^\circ .\)

Vậy \(\widehat {BAD} + \widehat {BCD} = 180^\circ \) .

Vậy trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng \(180^0\).

Câu 2: Cho tam giác \(ABC\) vuông tại \(A,(AB

a) \(CI\) là phân giác của \(\widehat{BCD}\)

b) \(DA\) là tiếp tuyến của \((O)\).

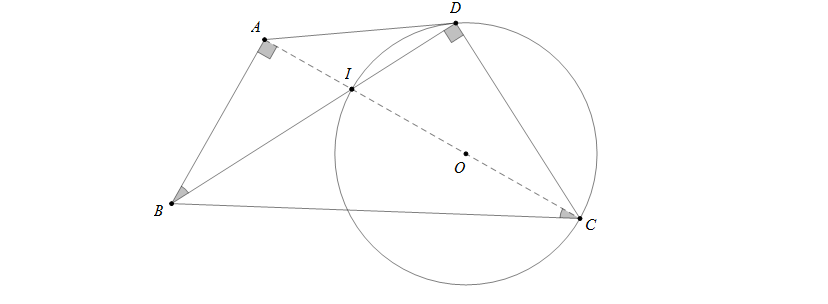
Hướng dẫn giải

a) Ta có \(\widehat{IDC}=90^0\) (góc nội tiếp chắn đường kính)

Nên \(\widehat{BAC}=\widehat{BDC}=90^0\) suy ra tứ giác \(ABCD\) nội tiếp 

do đó \(\widehat{ACD}=\widehat{ABD}\) mà theo đề bài \(\widehat{ABD}=\widehat{ACB}\) nên \(\widehat{ACD}=\widehat{ACB}\) hay \(CI\) là phân giác của \(\widehat{BCD}\) (đpcm)

b) Tứ giác \(ABCD\) nội tiếp nên \(\widehat{ADB}=\widehat{ACB}\) mà \(\widehat{ACD}=\widehat{ACB}\) nên \(\widehat{ADB}=\widehat{ACD}\)

Từ đó suy ra \(DA\) là tiếp tuyến của \((O)\).

Câu 1: Trên đường tròn tâm \(O\) có một cung \(AB\) và \(S\) là điểm chính giữa của cung đó. Trên dây \(AB\) lấy hai điểm \(E\) và \(H.\) Các đường thẳng \(SH\) và \(SE\) cắt đường tròn theo thứ tự tại \(C\) và \(D.\) Chứng minh \(EHCD\) là một tứ giác nội tiếp.

Câu 2: Cho tam giác \(ABC.\) Các đường phân giác trong của \(\widehat B\) và \(\widehat C\) cắt nhau tại \(S,\) các đường phân giác ngoài của \(\widehat B\) và \(\widehat C\) cắt nhau tại \(E.\) Chứng minh \(BSCE\) là một tứ giác nội tiếp.

Câu 3: Cho tam giác cân \(ABC\) có đáy \(BC\) và \(\widehat A = {20^0}\). Trên nửa mặt phẳng bờ \(AB\) không chứa điểm \(C\) lấy điểm \(D\) sao cho \(DA = DB\) và \(\widehat {DAB} = {40^0}\). Gọi \(E\) là giao điểm của \(AB\) và \(CD.\)

\(a)\) Chứng minh \(ACBD\) là tứ giác nội tiếp

\(b)\) Tính \(\widehat {AED}\)

Câu 4: Cho ba đường tròn cùng đi qua một điểm \(P.\) Gọi các giao điểm khác \(P\) của hai trong ba đường tròn đó là \(A, B, C.\) Từ một điểm \(D\) (khác điểm \(P\)) trên đường tròn \((PBC)\) kẻ các tia \(DB, DC\) cắt các đường tròn \((PAB)\) và \((PAC)\) lần lượt tại \(M, N.\) Chứng minh ba điểm \(M, A, N\) thẳng hàng.