Toán 9 Chương 3 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn

Góc có đỉnh nằm bên trong đường tròn được gọi là góc có đỉnh ở bên trong đường tròn.

Số đo của góc có đỉnh bên trong đường tròn bẳng nửa tổng số đo hai cung bị chắn.

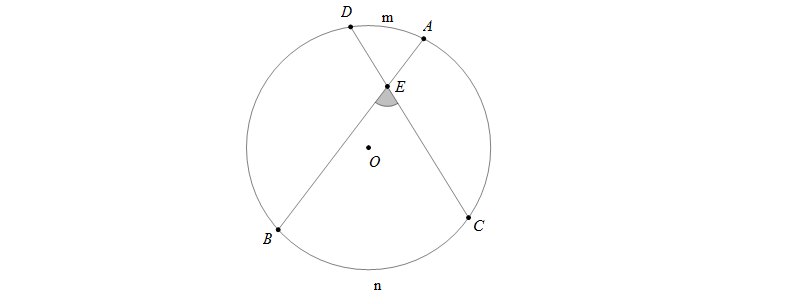
Góc $\widehat{BEC}$ là góc có đỉnh $E$ nằm bên trong đường tròn nên $\widehat{BEC}=\frac{1}{2}$(sđ$\stackrel\frown{BnC}$+sđ$\stackrel\frown{AmD}$)

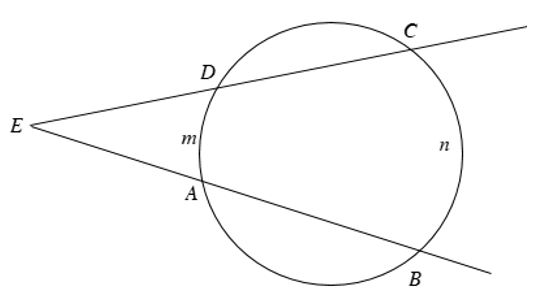
Góc có đỉnh ở bên ngoài đường tròn là góc có đỉnh nằm ngoài đường tròn và các cạnh đều có điểm chung với đường tròn.

Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

Góc $\widehat{AED}$ có đỉnh $E$ bên ngoài đường tròn nên $\widehat{AED}=\frac{1}{2}$(sđ$\stackrel\frown{BnC}-$sđ$\stackrel\frown{AmD}$)

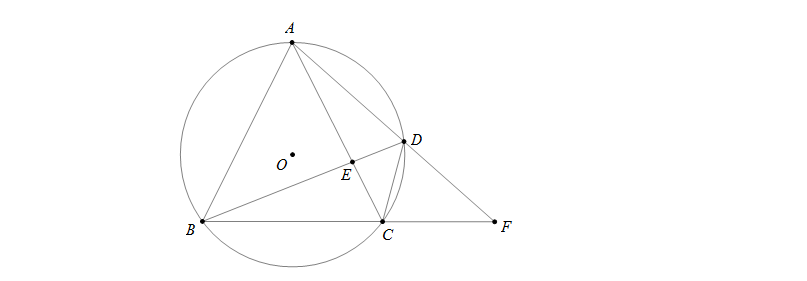
Câu 1: Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Điểm D di chuyển trên cung AC. E là diao điểm của AC và BD, F là giao điểm của AD và BC. Chứng minh $\widehat{AFB}=\widehat{ABD}$

Hướng dẫn giải

Do $\bigtriangleup ABC$ cân tại A nên AB=AC suy ra sđ$\stackrel\frown{AB}=$sđ$\stackrel\frown{AC}$

Ta có $\widehat{AFB}=\frac{1}{2}$(sđ$\stackrel\frown{AB}-$ sđ$\stackrel\frown{CD}$)$=\frac{1}{2}$(sđ$\stackrel\frown{AC}-$ sđ$\stackrel\frown{CD}$)$=\frac{1}{2}$sđ$\stackrel\frown{AD}$

Mặt khác $\widehat{ABD}=\frac{1}{2}$sđ$\stackrel\frown{AD}$, do đó $\widehat{AFB}=\widehat{ABD}$

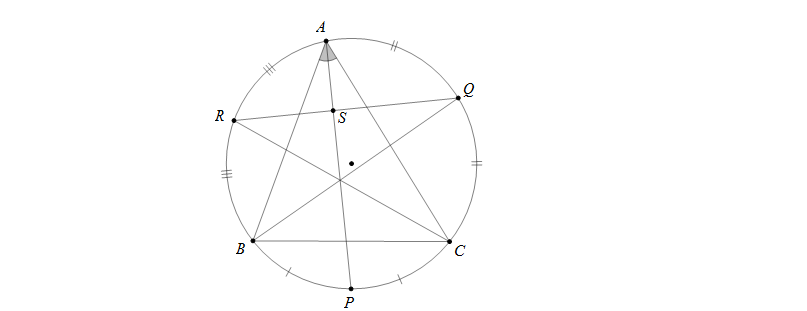
Câu 2: Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi P,Q,R lần lượt là giao điểm của các tia phân giác trong góc A,B,C với đường tròn. Chứng minh $AP\perp QR$

Hướng dẫn giải

Ta có tia phân giác AP chia đôi cung $\stackrel\frown{BC}$ thành hai cung bằng nhau, tức là $\stackrel\frown{BP}=\stackrel\frown{CP}$

Tương tự $\stackrel\frown{AQ}=\stackrel\frown{CQ},\stackrel\frown{AR}=\stackrel\frown{BR}$

Gọi S là giao điểm của AP và QR. Lúc đó $\widehat{ASQ}=\frac{1}{2}$(sđ$\stackrel\frown{AQ}+$sđ$\stackrel\frown{PR}$)$=\frac{1}{2}(\frac{1}{2}$sđ$\stackrel\frown{AC}$+$\frac{1}{2}$sđ$\stackrel\frown{AB}$+$\frac{1}{2}$sđ$\stackrel\frown{BC})$=$\frac{1}{2}.(\frac{1}{2}.360^0)=90^0$

Và do đó $AP\perp QR$

Câu 3: Cho tam giác nhọn ABC (AB>BC) nội tiếp đường tròn (O). D là điểm chính giữa cung AC. Gọi E,F lần lượt là giao điểm của AB và CD; AD và BC. Chứng minh rằng $\widehat{AED}<\widehat{CFD}$

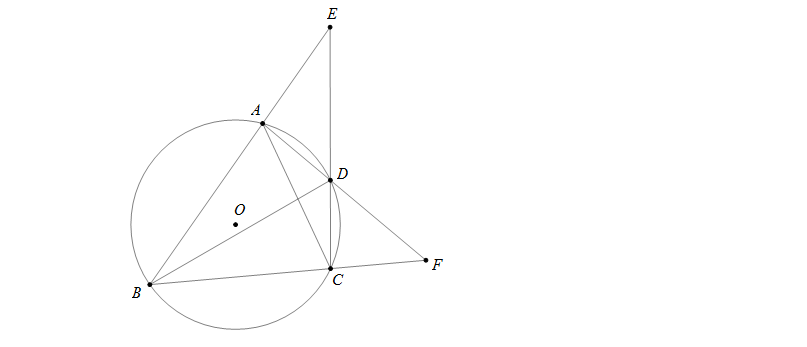
Hướng dẫn giải

Ta có: $\widehat{AED}=\frac{1}{2}$(sđ$\stackrel\frown{BC}-$sđ$\stackrel\frown{AD}$) và $\widehat{CFD}=\frac{1}{2}$(sđ$\stackrel\frown{AB}-$sđ$\stackrel\frown{CD}$)

Theo đề bài ta có sđ$\stackrel\frown{BC}<$sđ$\stackrel\frown{AB}$ (do AB>BC) và sđ$\stackrel\frown{AD}$=sđ$\stackrel\frown{CD}$ (do D là điểm chính giữa cung AC)

Suy ra$\widehat{AED}<\widehat{CFD}$

Câu 1: Cho tam giác đều ABC nội tiếp đường tròn tâm O. D là một điểm di dộng trên cung nhỏ AC. Gọi E là giao điểm của AC và BD, gọi F là giao điểm của AD và BC. Chứng minh tích AE.BF không phụ thuộc vào vị trí của D

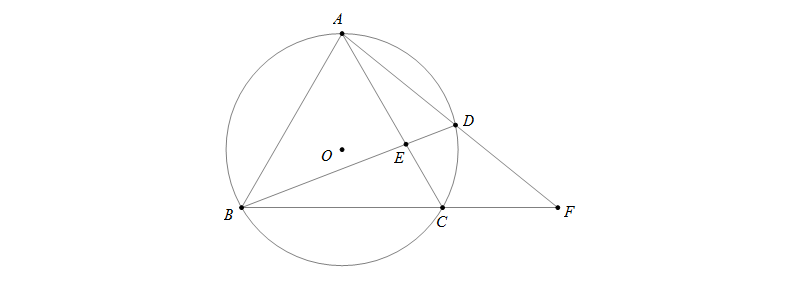
Hướng dẫn giải

Vì AB=AC nên sđ$\stackrel\frown{AB}=$sđ$\stackrel\frown{AC}$

Ta có $\widehat{AFB}=\frac{1}{2}$(sđ$\stackrel\frown{AB}-$ sđ$\stackrel\frown{CD}$)$=\frac{1}{2}$(sđ$\stackrel\frown{AC}-$ sđ$\stackrel\frown{CD}$)$=\frac{1}{2}$sđ$\stackrel\frown{AD}$

Mặt khác $\widehat{ABD}=\frac{1}{2}$sđ$\stackrel\frown{AD}$, do đó $\widehat{AFB}=\widehat{ABD}$

Xét $\bigtriangleup AFB$ và $\bigtriangleup EBA$ có $\widehat{AFB}=\widehat{ABD}$ (chứng minh trên) và $\widehat{FBA}=\widehat{BAE}=60^0$ ($\bigtriangleup ABC$ đều)

nên $\bigtriangleup AFB \sim\bigtriangleup EBA$ (g.g) suy ra $\frac{AB}{AE}=\frac{BF}{AB} \Rightarrow AE.BF=AB^2$ không đổi

Vậy tích AE.BF không phụ thuộc vào vị trí điểm D

Câu 2: Tứ giác ABCD có các góc B và D tù. Chứng minh AC>BD

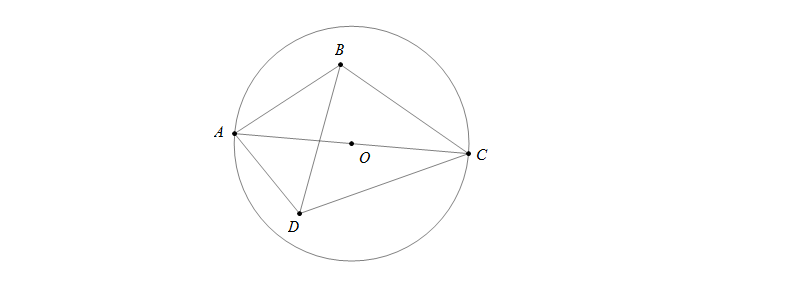
Hướng dẫn giải

Vẽ đường tròn tâm O đường kính AC.

Ta có $\widehat{ABC}>90^0, \widehat{ADC}>90^0$ nên B và D là hai điểm ở bên trong đường tròn (O)

suy ra BD nhỏ hơn dây cung chứa nó

Mặt khác đường kính AC là dây cung lớn nhất và do đó AC>BD

Câu 1: Cho tam giác ABC vuông ở A.Đường tròn đường kính AB cắt BC ở D .Tiếp tuyến ở D cắt AC ở P.Chứng minh rằng PD = PC

Câu 2: A, B, C là ba điểm thuộc đường tròn (O) sao cho tiếp tuyến tại A cắt tia BC tại D.Tia phân giác của góc (BAC) cắt đường tròn ở M,tia phân giác của góc D cắt AM ở I. Chứng minh DI ⊥ AM

Câu 3: Các điểm ${A_1},{A_2},....,{A_{19}},{A_{20}}$ được sắp xếp theo thứ tự đó trên đường tròn $(O)$ và chia đường tròn thành $20$ cung bằng nhau. Chứng minh rằng dây ${A_1}{A_8}$ vuông góc với dây ${A_3}{A_{16}}$.

Câu 4: Trên đường tròn $(O; R)$ vẽ ba dây liên tiếp bằng nhau $AB, BC, CD,$ mỗi dây có độ dài nhỏ hơn $R.$ Các đường thẳng $AB$ và $CD$ cắt nhau tại $I,$ các tiếp tuyến của đường tròn tại $B, D$ cắt nhau tại $K.$

$a)$ Chứng minh $\widehat {BIC} = \widehat {BKD}$

$b)$ Chứng minh $BC$ là tia phân giác của $\widehat {KBD}.$

Câu 1: Khẳng nào sau đây là đúng:

A. Số đo của góc có đỉnh bên trong đường tròn bằng nửa hiệu số đo hai cung bị chắn.

B. Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa tổng số đo hai cung bị chắn.

C. Góc có đỉnh trên đường tròn được gọi là góc nội tiếp và bằng góc ở tâm cùng chắn cung đó.

D. Góc nội tiếp chắn nửa đường tròn là góc vuông.

Câu 2: Cho đường tròn (O) và điểm E nằm ngoài đường tròn. Vẽ cát tuyến EAB và ECD với đường tròn (A nằm giữa E và B, C nằm giữa E và D). Gọi F là một điểm trên đường tròn sao cho B nằm chính giữa cung DF, I là giao điểm của FA và BC. Biết $\widehat{E}=25^0$, số đo góc $\widehat{I}$ là: 

A. 35⁰

B. 15⁰

C. 50⁰

D. 25⁰

Câu 3: Dựa vào hình vẽ sau, biết B là điểm chính giữa cung nhỏ AC, M là giao điểm của AD và BE và sđ$\stackrel\frown{BC}=30^0$, $\widehat{DCE}=30^0$. Lúc đó $\widehat{AMB}=?$

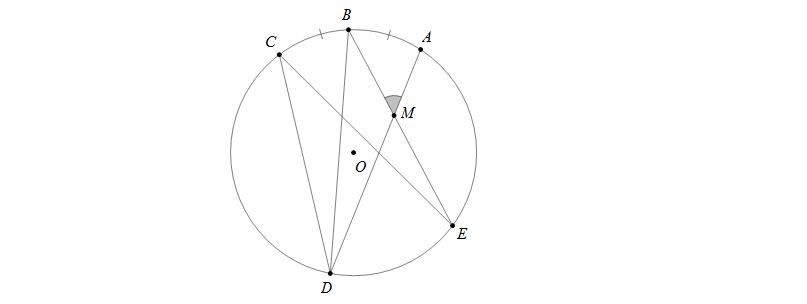
A. 90⁰

B. 60⁰

C. 45⁰

D. 50⁰

Câu 4: Cho đường tròn (O) và hai dây AB,CD của đường tròn sao cho AB cắt CD tại E. I là giao điểm của AD và BC. Cho $\widehat{E}=35^0$, sđ$\stackrel\frown{BD}=120^0$. Khi đó $\widehat{AIC}=?$

A. 75⁰

B. 85⁰

C. 100⁰

D. 110⁰

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Nhận biết được góc có đỉnh ở bên trong hay bên ngoài đường tròn dựa vào định nghĩa.
• Phát biểu và chứng minh được định lí về số đo của góc có đỉnh ở bên trong hay bên ngoài đường tròn.
• Phân chia được các trường hợp để tiến hành chứng minh.
• Bước đầu vận dụng được kiến thức vào giải bài tập.