Toán 9 Chương 3 Bài 6: Cung chứa góc
Bài học này trình bày nội dung lý thuyết và các bài tập quỹ tích, eLib đã tóm tắt lại hệ thống lý thuyết và hướng dẫn giải các bài tập một cách chi tiết, dễ hiểu. Sau đây mời các em cùng tham khảo.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Cách giải bài toán quỹ tích
Muốn chứng minh quỹ tích (tập hợp) các điểm M thỏa mãn tính chất \(\tau\) là một hình \(H\) nào đó, ta phải chứng minh hai phần:
Phần thuận: Mọi điểm có tính chất \(\tau\) đều thuộc hình \(H\).
Phần đảo: Mọi điểm thuộc hình \(H\) đều có tính chất \(\tau\).
Kết luận: Quỹ tích (hay tập hợp) các điểm M có tính chất \(\tau\) là hình \(H\)
Nhận xét: Một bài toán quỹ tích sẽ dễ có hướng xử lí hơn khi ta dự đoán được hình \(H\) trước khi bắt đầu chứng minh
1.2. Bài toán quỹ tích "Cung chứa góc"
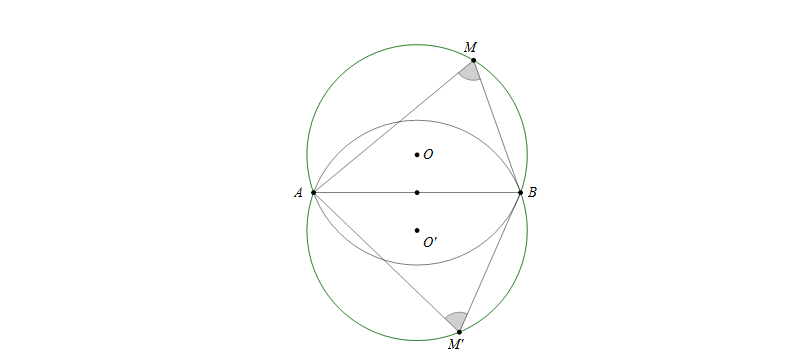
Với đoạn thẳng \(AB\) và góc \(\alpha(0^0<\alpha<180^0)\) cho trước thì quỹ tích các điểm \(M\) thỏa mãn \(\widehat{AMB}=\alpha\) là hai cung chứa góc \(\alpha\) dựng trên đoạn \(AB\)
Chú ý:
- Hai cung chứa góc \(\alpha\) nói trên là hai cung đối xứng với nhau qua \(AB\)
- Hai điểm \(A,B\) được coi là thuộc quỹ tích
- Trường hợp \(\alpha=90^0\) thì quỹ tích trên là hai nửa đường tròn đường kính \(AB\)
Áp dụng cung chứa góc vào chứng minh bốn điểm cùng thuộc một đường tròn: Nếu một tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc \(\alpha\) thì bốn đỉnh của tứ giác ấy cùng thuộc một đường tròn.
1.3. Cách vẽ cung chứa góc α
– Vẽ đường trung trực d của đoạn thẳng AB.
– Vẽ tia Ax tạo với AB một góc α.
– Vẽ đường thẳng Ay vuông góc với Ax. Gọi O là giao điểm của Ay với d.
– Vẽ cung AmB, tâm O, bán kính OA sao cho cung này nằm ở nửa mặt phẳng bờ AB không chứa tia Ax.
– Cung AmB được vẽ như trên là một cung chứa góc α.
2. Bài tập minh hoạ
2.1. Bài tập cơ bản
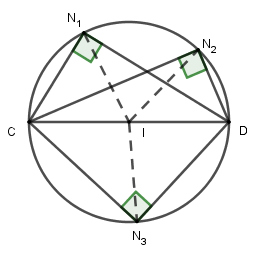
Câu 1: Cho đoạn thẳng \(CD\).
a) Vẽ ba điểm \(N_1;N_2;N_3\) sao cho \( \widehat {CN_1D}=\widehat {CN_2D}=\widehat {CN_3D}=90^0\)
b) Chứng minh rằng các điểm \(N_1;N_2;N_3\) nằm trên đường tròn đường kính \(CD.\)
Hướng dẫn giải
a) Vẽ hình.
b) Gọi \(I\) là trung điểm cạnh \(CD.\)
Vì tam giác \(C{N_1}D\) vuông tại \({N_1}\) nên \(I{N_1} = IC = ID = \dfrac{{CD}}{2}\)
Tương tự với hai tam giác vuông \(C{N_2}D;C{N_3}D\) ta có \(I{N_2} = I{N_3} = IC = ID = \dfrac{{CD}}{2}\)
Vậy \(I{N_1} = I{N_2} = I{N_3} = \dfrac{{CD}}{2}\) hay \({N_1};{N_2};{N_3}\) thuộc đường tròn đường kính \(CD.\)
Câu 2: Cho hình thang ABCD (AB//CD), O là giao điểm hai đường chéo. Trên tia OA lấy điểm M sao cho OM=OB. Trên tia OB lấy điểm M sao cho ON=OA. Chứng minh rằng: bốn điểm D,M,N,C cùng thuộc một đường tròn.
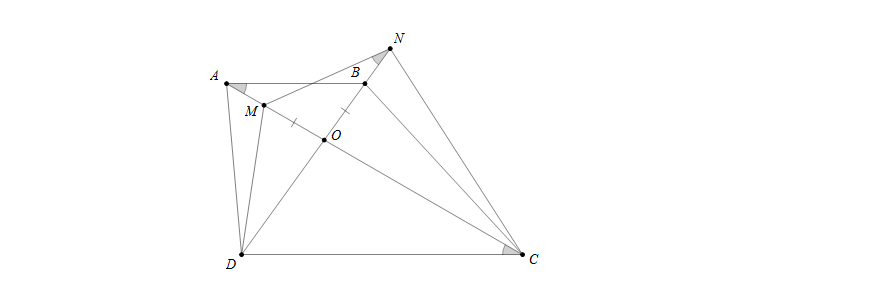
Hướng dẫn giải
Xét hai tam giác \(\bigtriangleup AOB\) và \(\bigtriangleup NOM\) có \(\widehat{AOB}\) chung và OA=ON; OM=OB
nên \(\bigtriangleup AOB=\bigtriangleup NOM\)(c.g.c)
suy ra \(\widehat{BAO}=\widehat{MNO}\)
Mặt khác do AB//CD (hình thang) nên \(\widehat{BAO}=\widehat{DCO}\), từ đó suy ra \(\widehat{MNO}=\widehat{DCO}\)
Xét tứ giác DMNC có \(\widehat{MNO}=\widehat{DCO}\) mà hai góc này cùng nhìn cạnh MD nên bốn điểm D,M,N,C cùng thuộc một đường tròn.
2.2. Bài tập nâng cao
Câu 1: Cho cung AB cố định tạo bởi các bán kính OA,OB vuông góc với nhau, điểm I chuyển động trên cung AB. Trên tia OI lấy điểm M sao cho OM bằng tổng các khoảng cách từ I đến OA và OB. Tìm quỹ tích các điểm M.
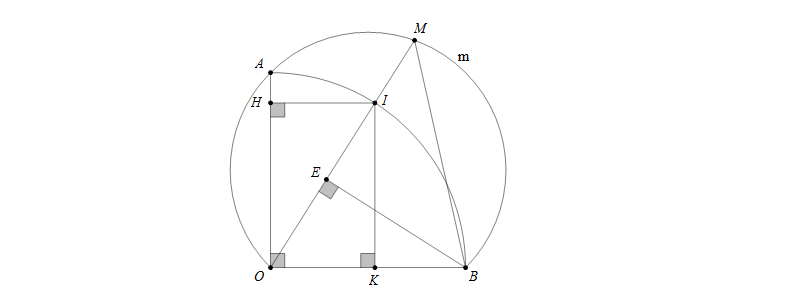
Hướng dẫn giải
Phần thuận: Kẻ \(IH\perp OA,IK\perp OB\), điểm M thuộc OI có tính chất OM=IH+IK (1)
Kẻ \(BE\perp OI\). Ta có \(\bigtriangleup OBE=\bigtriangleup OIK\) (cạnh huyền -góc nhọn) nên OE=OK=IH, BE=IK (2)
Từ (1) và (2) suy ra OM=IH+IK=OE+BE và do đó EM=EB
Suy ra tam giác EMB vuông cân tại E nên \(\widehat{EMB}=45^0\). Điểm M nhìn OB cố định dới góc \(45^0\) nên M di chuyển trên cung chứa góc \(45^0\) dựng trên OB.
Mặt khác, vì điểm M chỉ nằm bên trong góc vuông AOB nên M chỉ di chuyển trên cung AmB, một phần của cung chứa góc \(45^0\) dựng trên OB.
Phần đảo: Lấy điểm M bất kì trên cung AmB. Kẻ \(BE\perp OM,IH\perp OA, IK\perp OB\) ta sẽ chứng minh OM=IH+IK
Thật vậy, ta làm ngược lại với phần thuận
Do \(\widehat{OMB}=45^0\) nên tam giác EMB vuông cân tại E, suy ra EM=EB
\(\bigtriangleup OBE=\bigtriangleup OIK\) (cạnh huyền -góc nhọn) nên OE=OK=IH, BE=IK. Do đó EM=IK
Vậy OM=OE+EM=IH+IK
Kết luận: Quỹ tích (tập hợp) các điểm M là cung AmB, một phần của cung chứa góc \(45^0\) dựng trên đoạn OB nằm bên trong góc vuông AOB.
Câu 2: Cho nửa đường tròn (O) đường kính AB. C là một điểm trên nửa đường tròn. Trên bán kính OC lấy điểm D sao cho OD bằng khoảng cách từ C đến AB.
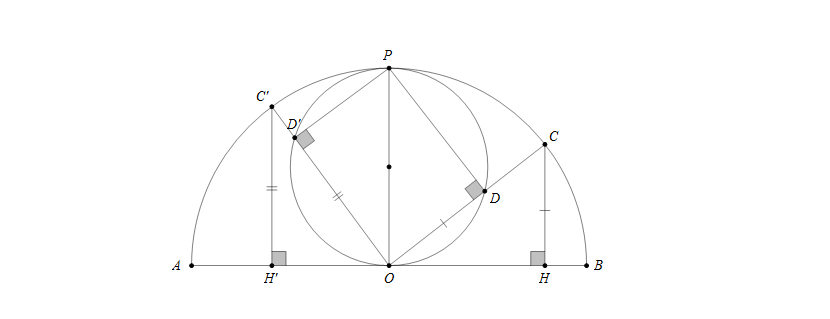
Hướng dẫn giải
Phần thuận: Vẽ \(OP\perp AB\) với P thuộc (O)
Xét \(\bigtriangleup OPD\) và \(\bigtriangleup COH\) có
OD=OH (giả thiết)
OP=OC (cùng bằng bán kính nửa đường tròn)
\(\widehat{POD}=\widehat{OCH}\) (so le trong)
Nên \(\bigtriangleup OPD=\bigtriangleup {COH}\) (c.g.c) suy ra \(\widehat{ODP}=90^0\)
Mặt khác ta có O,P cố định nên D nằm trên đường tròn đường kính OP
Phần đảo: Lấy điểm D' bất kì nằm trên đường tròn đường kính OP, tia OD' cắt (O) tại C'. Hạ đường vuông góc C'H' xuống AB. Ta sẽ chứng minh OD'=C'H'
Thật vậy, xét hai tam giác vuông OD'P và C'H'O có cạnh huyền OP=OC' và một góc nhọn \(\widehat{POD'}=\widehat{OC'H'}\)(so le trong)
Nên \(\bigtriangleup OD'P=\bigtriangleup C'H'O\) (cạnh huyền - góc nhọn) suy ra OD'=CH'
Kết luận: Quỹ tích (tập hợp) các điểm D khi C chạy trên nửa đường tròn đường kính AB là đường tròn đường kính OP với P là điểm chính giữa cung AB.
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho tam giác \(ABC\) có cạnh \(BC\) cố định và \(\widehat A = \alpha \) không đổi. Tìm quỹ tích giao điểm của ba đường phân giác trong của tam giác đó
Câu 2: Dựng tam giác \(ABC,\) biết \(BC = 3 cm,\) \(\widehat A = {45^o}\) và trung tuyến \(AM = 2,5 cm.\)
Câu 3: Cho nửa đường tròn đường kính \(AB\) cố định. \(C\) là điểm trên nửa đường tròn, trên dây \(AC\) kéo dài lấy điểm \(D\) sao cho \(CD = CB.\)
\(a)\) Tìm quỹ tích các điểm \(D\) khi \(C\) chạy trên nửa đường tròn đã cho.
\(b)\) Trên tia \(CA\) lấy điểm \(E\) sao cho \(CE = CB.\) Tìm quỹ tích các điểm \(E\) khi \(C\) chạy trên nửa đường tròn đã cho.
Câu 4: Cho nửa đường tròn đường kính \(AB\) và \(C\) là một điểm trên nửa đường tròn. Trên bán kính \(OC\) lấy điểm \(D\) sao cho \(OD\) bằng khoảng cách \(CH\) từ \(C\) đến \(AB.\) Tìm quỹ tích các điểm \(D\) khi \(C\) chạy trên nửa đường tròn đã cho.
3.2. Bài tập trắc nghiệm
Câu 1: Quỹ tích các điểm M nhìn đoạn thẳng AB dưới một góc 1200 là:
A. Một đường tròn đi qua hai điểm A,B
B. Một đường thẳng song song với AB
C. Một cung chứa góc 1200 dựng trên hai điểm A,B
D. Hai cung chứa góc 1200 đối xứng nhau dựng trên hai điểm A,B
Câu 2: Cho đường thẳng d,một điểm C nằm ngoài đường thẳng d và cách d một khoảng là 5cm. Tập hợp các điểm trên d cách C một khoảng là 6cm là
A. Hai điểm trên d cách C một khoảng 6cm
B. Không có điểm nào
C. Là đường thẳng d
D. Một điểm trên d cách C một khoảng 6cm.
Câu 3: Khẳng định nào sau đây là sai:
A. Tập hợp các điểm cách đều hai đầu mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó
B. Tập hợp các điểm nằm bên ngoài một góc cho trước và cách đều hai tia của góc đó là đường phân giác trong kẻ từ đỉnh của góc đó.
C. Tập các điểm cách điều một điểm cho trước là đường tròn với tâm là điểm đã cho
D. Với đoạn thẳng \(AB\) và góc \(\alpha(0^0<\alpha<180^0)\) cho trước thì quỹ tích các điểm \(M\) thỏa mãn \(\widehat{AMB}=\alpha\) là hai cung chứa góc \(\alpha\) dựng trên đoạn \(AB\)
Câu 4: Cho tam giác ABC vuông tại A, có cạnh BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Quỹ tích điểm I khi A thay đổi là:
A. Đường tròn đường kính BC
B. Đường thẳng song song với BC
C. Một cung chứa góc 1350 dựng trên đoạn BC (nằm cùng phía với A so với BC)
D. Hai cung chứa góc 1350 dựng trên đoạn BC
4. Kết luận
Qua bài học này, các em nắm được một số nội dung chính như sau:
- Quỹ tích cung chứa góc, vận dụng cặp mệnh đề thuận, đảo của quỹ tích này để giải bài toán.
- Sử dụng đúng thuật ngữ “cung chứa góc” dựng trên một đoạn thẳng và vẽ cung chứa góc trên đoạn thẳng cho trước.
- Giải được bài toán quỹ tích gồm hai phần thuận, đảo và kết luận.
Tham khảo thêm
- doc Toán 9 Chương 3 Bài 1: Góc ở tâm và số đo cung
- doc Toán 9 Chương 3 Bài 2: Liên hệ giữa cung và dây
- doc Toán 9 Chương 3 Bài 3: Góc nội tiếp
- doc Toán 9 Chương 3 Bài 4: Góc tạo bởi tia tiếp tuyến và dây cung
- doc Toán 9 Chương 3 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
- doc Toán 9 Chương 3 Bài 7: Tứ giác nội tiếp
- doc Toán 9 Chương 3 Bài 8: Đường tròn ngoại tiếp và đường tròn nội tiếp
- doc Toán 9 Chương 3 Bài 9: Độ dài đường tròn, cung tròn
- doc Toán 9 Chương 3 Bài 10: Diện tích hình tròn, hình quạt tròn
- doc Toán 9 Ôn tập chương 3: Góc với đường tròn