Toán 9 Chương 3 Bài 8: Đường tròn ngoại tiếp và đường tròn nội tiếp

1. Tóm tắt lý thuyết

- Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác và đa giác này gọi là nội tiếp đường tròn.

- Đường tròn tiếp xúc với tất cả các cạnh của một đa giác được gọi là đường tròn  nội tiếp đa giác và đa giác được gọi là ngoại tiếp đường tròn.

Đa giác đều nào cũng có một đường tròn ngoại tiếp, một đường tròn nội tiếp. Tâm của hai đường tròn này trùng nhau và được gọi là tâm của đa giác đều

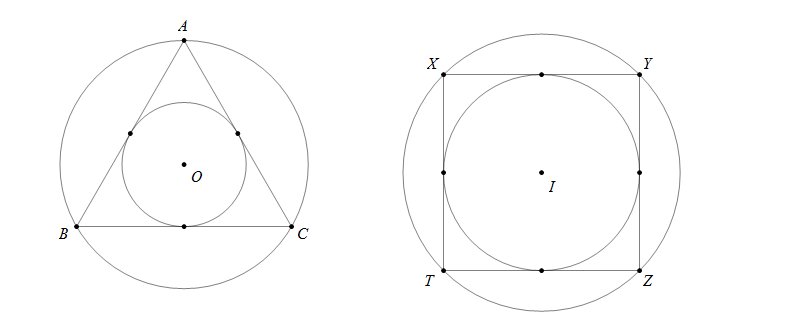
- Tam giác ABC đều có tâm đường tròn nội tiếp và ngoại tiếp trùng nhau

- Hình vuông XYZT có tâm đường tròn nội tiếp và ngoại tiếp trùng nhau

Đa giác đều \(n\) cạnh có độ dài mỗi cạnh là \(a, R\) là bán kính đường tròn ngoại tiếp và \(r\) là bán kính đường tròn nội tiếp đa giác.

Ta có: \( R\) = \(\dfrac{a}{2sin\dfrac{180^{\circ}}{n}}\); \(r\) = \(\dfrac{a}{2tan\dfrac{180^{\circ}}{n}}\).

Câu 1: 

a) Vẽ đường tròn tâm O bán kính R = 2cm.

b) Vẽ một lục giác đều ABCDEF có tất cả các đỉnh nằm trên đường tròn (O).

c) Vì sao tâm O cách đều các cạnh của lục giác đều ? Gọi khoảng cách này là r.

d) Vẽ đường tròn (O; r).

Hướng dẫn giải

a)

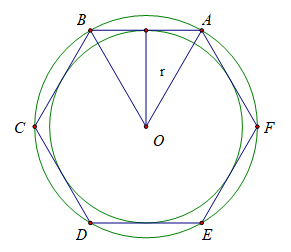
b) Cách vẽ lục giác đều có tất cả các đỉnh nằm trên đường tròn (O)

Vẽ các dây cung AB = BC = CD = DE = EF = FA = R = 2 cm

c) Vì các dây cung AB = BC = CD = DE = EF = FA bằng nhau nên khoảng cách từ O đến các dây là bằng nhau

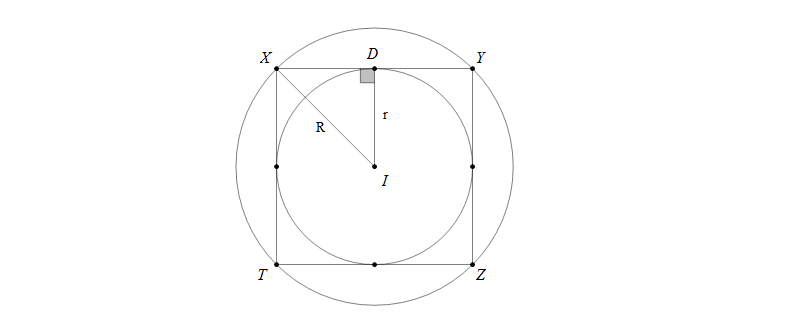
Câu 2: Cho hình vuông XYZT có tâm I. Tính chu vi đường tròn ngoại tiếp của hình vuông biết chu vi đường tròn nội tiếp của hình vuông XYZT là \(20\pi\)(cm)

Hướng dẫn giải

Đặt \(R,r (cm)\) lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp của hình vuông XYZT.

Theo đề bài, chu vi đường tròn nội tiếp của hình vuông XYZT là \(20\pi\)(cm) nên \(2r.\pi=20\Rightarrow r=10 cm\)

Vẽ \(ID\perp XY (D\in XY)\)

Khi đó tam giác IXD vuông cân tại D, áp dụng định lí Pytago ta có \(R^2=2r^2\Rightarrow R=\sqrt{2.10^2}=10\sqrt{2} cm\)

Chu vi đường tròn ngoại tiếp của hình vuông là: \(2\pi R=20\sqrt{2} \pi (cm)\)

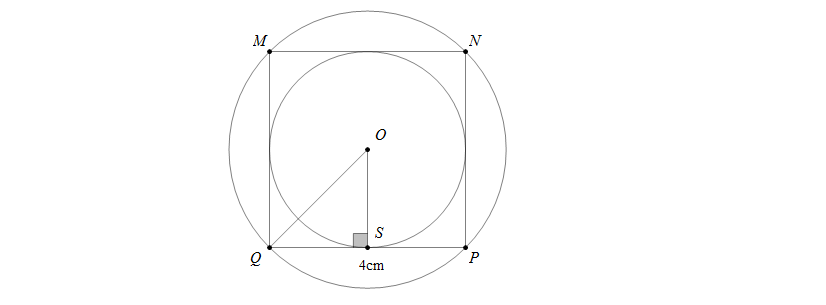
Câu 3: Cho hình vuông MNPQ có cạnh bằng 4cm. Tính diện tích hình vuông, diện tích hình tròn nội tiếp và ngoại tiếp hình vuông MNPQ.

Hướng dẫn giải

Diện tích hình vuông MNPQ là: \(S_{MNPQ}=4^2=16(cm^2)\)

Kẻ \(OS\perp PQ (S\in PQ)\) thì \(SQ=SP=2cm\)

Dễ chứng minh tam giác OSQ vuông cân tại S

Áp dụng định lí Pytago cho tam giác vuông cân OSQ ta có \(OQ=\sqrt{2.OS^2}=2\sqrt{2}(cm)\)

Diện tích hình tròn nội tiếp hình vuông là: \(S_{1}=OS^2.\pi=4\pi (cm^2)\)

Diện tích hình tròn ngoại tiếp hình vuông là: \(S_{2}=OQ^2.\pi=(2\sqrt{2})^2\pi=8\pi (cm^2)\)

Câu 1: Chứng minh rằng: Trong hình vuông, bán kính đường tròn ngoại tiếp luôn lớn hơn bán kính đường tròn nội tiếp của hình vuông đó.

Hướng dẫn giải

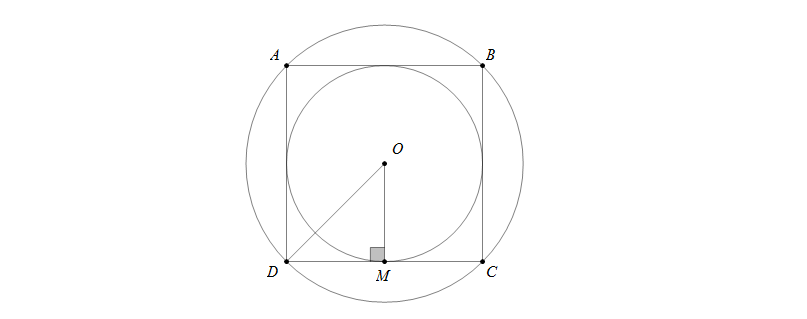
Xét hình vuông ABCD có tâm O, kẻ \(OM\perp CD (M\in CD)\)

Lúc đó OD là bán kính đường tròn ngoại tiếp, OM là bán kính đường tròn nội tiếp hình vuông ABCD

\(\bigtriangleup OMD\) vuông tại M nên \(OD\geq OM\) (1)

Giả sử \(OD= OM\) khi đó đường tròn nội tiếp và đường tròn ngoại tiếp là hai đường tròn có chung tâm O và độ dài hai bán kính bằng nhau nên chúng trùng nhau.

Lúc đó không tồn tại hình vuông vừa có đỉnh trên đường tròn (O) vừa có cạnh tiếp xúc với đường tròn (O)

Do đó \(OD\neq OM\) kết hợp với (1) ta có \(OD> OM\) (đpcm)

Câu 2: Cho lục giác đều ABCDEF có tâm O. Đặt R,r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp lục giác. Viết biểu thức liên hệ giữa R và r.

Hướng dẫn giải

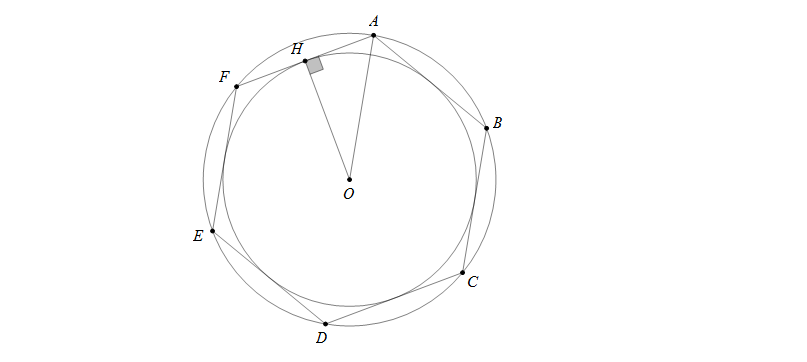
Lục giác ABCDEF đều nên chia đường tròn ngoại tiếp (O) thành 6 cung bằng nhau, suy ra \(\widehat{AOF}=\frac{360^0}{6}=60^0\)

Tam giác AOF cân tại O có \(\widehat{AOF}=60^0\) nên \(\bigtriangleup AOF\) đều.

Vẽ đường cao AH của \(\bigtriangleup AOF\) khi đó \(OH=r\) và \(AH=\frac{R}{2}\)

\(\bigtriangleup AOH\) vuông tại H nên \(AO^2=OH^2+AH^2\Rightarrow R^2=r^2+(\frac{R}{2})^2\Rightarrow r^2=\frac{3R^2}{4}\Rightarrow r=\frac{R\sqrt{3}}{2}\)

Câu 1: Vẽ hình vuông \(ABCD\) tâm \(O\) rồi vẽ tam giác đều có một đỉnh là \(A\) và nhận \(O\) làm tâm. Nêu cách vẽ.

Câu 2: Vẽ đường tròn tâm \(O\) bán kính \(R = 2cm\) rồi vẽ hình tám cạnh đều nội tiếp đường tròn \((O; 2 cm).\) Nêu cách vẽ.

Câu 3: 

\(a)\) Vẽ một lục giác đều \(ABCDEG\) nội tiếp đường tròn bán kính \(2cm\) rồi vẽ hình \(12\) cạnh đều \(AIBJCKDLEMGN\) nội tiếp đường tròn đó. Nêu cách vẽ.

\(b)\) Tính độ dài cạnh \(AI.\)

\(c)\) Tính bán kính \(r\) của đường tròn nội tiếp hình \(AIBJCKDLEMGN.\)

Hướng dẫn. Áp dụng các công thức ở bài \(46.\)

Câu 4: 

\(a)\) Tính cạnh của một ngũ giác đều nội tiếp đường tròn bán kính \(3cm.\)

\(b)\) Tính cạnh của một ngũ giác đều ngoại tiếp đường tròn bán kính \(3cm.\) 

Câu 1: Tam giác đều ABC có tâm (O), bán kính đường tròn ngoại tiếp của tam giác là 12cm. Khi đó, chu vi tam giác là:

A. \(12\sqrt{3}(cm)\)

B. \(24\sqrt{3}(cm)\)

C. \(36\sqrt{3}(cm)\)

D. \(48\sqrt{3}(cm)\)

Câu 2: Phát biểu nào sau đây là sai:

A. Hình vuông luôn nội tiếp được đường tròn.

B. Tam giác luôn nội tiếp được đường tròn

C. Ngũ giác đều luôn có đường tròn nội tiếp và ngoại tiếp

D. Trong hình vuông, đặt R,r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp hình vuông. Khi đó R=2r

Câu 3: Khẳng định nào sau đây là đúng:

A. Bất cứ đa giác nào cũng có đường tròn nội tiếp, đường tròn ngoại tiếp.

B. Bán kính đường tròn nội tiếp của một hình vuông luôn lớn hơn bán kính đường tròn ngoại tiếp hình vuông đó.

C. Đa giác bất kì đều có tâm đường tròn ngoại tiếp và đường tròn nội tiếp trùng nhau.

D. Tam giác luôn luôn có đường tròn nội tiếp và đường tròn ngoại tiếp.

Câu 4: Cho hình vuông ABCD có tâm O. Gọi R,r là bán kính đường tròn ngoại tiếp và nội tiếp hình vuông ABCD. Biết \(R+r=3\sqrt{2}(cm)\). Tính chu vi đường tròn nội tiếp hình vuông ABCD.

A. \((12-6\sqrt{2})\pi (cm)\)

B. \((18-6\sqrt{2}) \pi (cm)\)

C. \(8 (cm)\)

D. \(12-6\sqrt{2} (cm)\)

Câu 5: Cho lục giác ABCDEF đều có bán kính đường tròn ngoại tiếp là \(2\sqrt{3} (cm)\). Bán kính đường tròn nội tiếp lục giác này là:

A. \(\frac{3\sqrt{2}}{2} (cm)\)

B. \(4 (cm)\)

C. \(3\sqrt{2}(cm)\)

D. \(3(cm)\)

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Phát biểu được định nghĩa, tính chất của đường tròn ngoại tiếp, đường tròn nội tiếp một đa giác.
• Nhận biết được bất cứ một đa giác đều nào cũng có một đường tròn ngoại tiếp và một đường tròn nội tiếp.
• Vẽ được tâm của đa giác đều, từ đó vẽ được đường tròn ngoại tiếp và đường tròn nội tiếp của một đa giác đều cho trước.
• Tính được cạnh a theo R và ngược lại tính được R theo cạnh a của tam giác đều, hình vuông, lục giác đều.