Giải bài tập SBT Toán 12 Bài 1: Sự đồng biến, nghịch biến của hàm số
Giải bài tập trang 7, 8, 9 SBT Toán 12 Bài Sự đồng biến, nghịch biến của hàm số giúp các em học sinh sẽ dễ dàng ôn tập lại các kiến thức đã học, rèn luyện khả năng tính toán nhanh và chính xác. Sau đây mời các em cùng tham khảo lời giải tương ứng với từng bài tập SBT.
Mục lục nội dung
1. Giải bài 1.1 trang 7 SBT Giải tích 12
2. Giải bài 1.2 trang 7 SBT Giải tích 12
3. Giải bài 1.3 trang 8 SBT Giải tích 12
4. Giải bài 1.4 trang 8 SBT Giải tích 12
5. Giải bài 1.5 trang 8 SBT Giải tích 12
6. Giải bài 1.6 trang 8 SBT Giải tích 12
7. Giải bài 1.7 trang 8 SBT Giải tích 12
8. Giải bài 1.8 trang 8 SBT Giải tích 12
9. Giải bài 1.9 trang 8 SBT Giải tích 12
10. Giải bài 1.10 trang 8 SBT Giải tích 12
11. Giải bài 1.11 trang 9 SBT Giải tích 12
12. Giải bài 1.12 trang 9 SBT Giải tích 12
13. Giải bài 1.13 trang 9 SBT Giải tích 12
14. Giải bài 1.14 trang 9 SBT Giải tích 12

1. Giải bài 1.1 trang 7 SBT Giải tích 12
Xét sự đồng biến, nghịch biến của các hàm số sau:
|
a) \(y=3x^2-8x^3\); |
b) \(y=16x+2x^2-\dfrac{16}{3}x^3-x^4\); |
|
c) \(y=x^3-6x^2+9x\); |
d) \(y=x^4+8x^2+5\). |
Phương pháp giải
- Tính y'
- Tìm nghiệm của phương trình y'=0
- Xét dấu y' và kết luận.
Hướng dẫn giải
a) \(y=3x^2-8x^3\). TXĐ: \(\mathbb{R}\)
\(y'=6x-24x^2=6x(1-4x) \\ y'=0 \Leftrightarrow \left[ \begin{align} & x=0 \\ & x=\frac{1}{4} \\ \end{align} \right. \)
Bảng biến thiên:
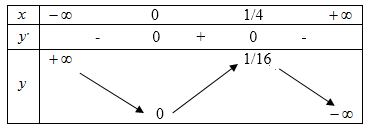
\(y'>0\) trên khoảng \(\left( 0;\dfrac{1}{4} \right) \), suy ra y đồng biến trên khoảng \(\left( 0;\dfrac{1}{4} \right) \)
\(y'<0\) trên khoảng \(\left( -\infty ;0 \right)\,;\,\,\left( \dfrac{1}{4};+\infty \right) \), suy ra y nghịch biến trên từng khoảng \(\left( -\infty ;0 \right)\,;\,\,\left( \dfrac{1}{4};+\infty \right) \)
b) \(y=16x+2x^2-\dfrac{16}{3}x^3-x^4\). TXĐ: \(\mathbb{R}\)
\(\begin{aligned} & y'=16+4x-16{{x}^{2}}-4{{x}^{3}}=-4\left( x+4 \right)\left( {{x}^{2}}-1 \right) \\ & y'=0\Leftrightarrow \left[ \begin{aligned} & x=-4 \\ & x=-1 \\ & x=1 \\ \end{aligned} \right. \\ \end{aligned} \)

Vậy hàm số y đã cho đồng biến trên các khoảng \( \left( -\infty ;-4 \right)\) và \((-1;1)\), nghịch biến trên các khoảng \((-4;-1)\) và \((1;+\infty)\).
c) \(y=x^3-6x^2+9x\). TXĐ: \(\mathbb{R}\)
\(\begin{aligned} & y'=3{{x}^{2}}-12x+9 \\ & y'=0\Leftrightarrow \left[ \begin{aligned} & x=0 \\ & x=3 \\ \end{aligned} \right. \\ \end{aligned} \)

\(y'>0\) trên các khoảng \((-\infty;1), (3;+\infty)\)nên y đồng biến trên các khoảng \((-\infty;1), (3;+\infty)\)
y'<0 trên khoảng (1;3) nên y nghịch biến trên khoản (1;3)
d) \(y=x^4+8x^2+5\). TXĐ: \(\mathbb{R}\)
\(\begin{align} & y'=4{{x}^{3}}+16x=4x\left( {{x}^{2}}+4 \right) \\ & y'=0\Leftrightarrow x=0 \\ \end{align} \)

\(y'>0\) trên khoảng \((0;+\infty)\) nên y đồng biến trên khoảng \((0;+\infty)\)
\(y'<0\) trên khoảng \((-\infty;0)\) nên y nghịch biến trên khoảng \((-\infty;0)\).
2. Giải bài 1.2 trang 7 SBT Giải tích 12
Tìm các khoảng đồng biến, nghịch biến của các hàm số sau:
|
a) \(y=\dfrac{3-2x}{x+7}\); |
b) \(y=\dfrac{1}{(x-5)^2}\); |
|
c) \(y=\dfrac{2x}{x^2-9}\); |
d) \(y=\dfrac{x^4+48}{x}\); |
|
e) \(y=\dfrac{x^2-2x+3}{x+1}\); |
g) \(y=\dfrac{x^2-5x+3}{x-2}\). |
Phương pháp giải
- Tìm TXĐ.
- Tính y' theo công thức \(\left( {\dfrac{{ax + b}}{{cx + d}}} \right)' = \dfrac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}\)
- Xét dấu y' và kết luận khoảng đồng biến, nghịch biến.
Hướng dẫn giải
a) \(y=\dfrac{3-2x}{x+7}\). TXĐ: \(\mathbb{R}\)\ {-7}.
\(y'=\dfrac{-17}{(x+7)^2}\).
\(y'<0\) trên các khoảng \((-\infty;-7), (-7;+\infty)\) nên hàm số nghịch biến trên các khoảng đó.
b) \(y=\dfrac{1}{(x-5)^2}\). TXĐ: \(\mathbb{R}\)\ {5}
\(y'=\dfrac{-2}{(x-5)^3}\).
\(y'<0\) trên khoảng \((5;+\infty)\) nên y nghịch biến trên khoảng \((5;+\infty)\).
\(y'>0\) trên khoảng \((-\infty;5)\) nên y đồng biến trên khoảng \((-\infty;5)\).
c) \(y=\dfrac{2x}{x^2-9}\). TXĐ: \(\mathbb{R}\)\{-3;3}
\(y'=\dfrac{-2(x^2+9)}{(x^2-9)^2}\)
\(y'<0\) trên các khoảng \((-\infty;-3), (-3;3), (3;+\infty)\) nên hàm số nghịch biến trên các khoảng đó.
d) \(y=\dfrac{x^4+48}{x}\). TXĐ: \(\mathbb{R}\)\{0}
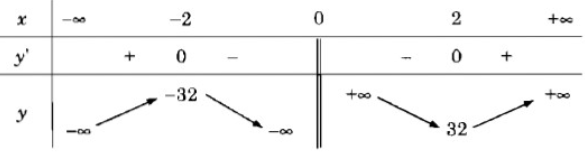
\(\begin{aligned} & y'=\dfrac{3\left( {{x}^{4}}-16 \right)}{{{x}^{2}}}=\dfrac{3\left( {{x}^{2}}-4 \right)\left( {{x}^{2}}+4 \right)}{{{x}^{2}}} \\ & y'=0\Leftrightarrow \left[ \begin{aligned} & x=-2 \\ & x=2 \\ \end{aligned} \right. \\ \end{aligned} \)
Bảng biến thiên:
Vậy hàm số đã cho đồng biến trên các khoảng \((-\infty;-2), (2;+\infty)\) và nghịch biến trên các khoảng \((-2;0), (0;2)\).
e) \(y=\dfrac{x^2-2x+3}{x+1}\). TXĐ: \(\mathbb{R}\)\{-1}
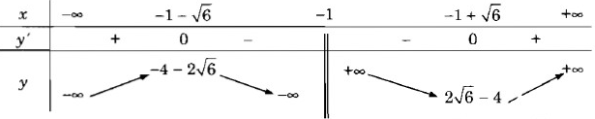
\(\begin{aligned} & y'=\dfrac{{{x}^{2}}+2x-5}{{{\left( x+1 \right)}^{2}}} \\ & y'=0\Leftrightarrow \left[ \begin{aligned} & x=-1-\sqrt{6} \\ & x=-1+\sqrt{6} \\ \end{aligned} \right. \\ \end{aligned} \)
Bảng biến thiên:
Vậy hàm số đồng biến trên các khoảng \((-\infty;-1-\sqrt{6}), (-1+\sqrt{6};+\infty)\) và nghịch biến trên các khoảng \((-1-\sqrt{6};-1),(-1;-1+\sqrt{6})\).
g) \(y=\dfrac{x^2-5x+3}{x-2}\). TXĐ: \(\mathbb{R}\)\{2}
\(y'=\dfrac{x^2-4x+7}{(x-2)^2}>0\) (do \(x^2-4x+7\) có \(\Delta' =-3 <0\))
Vậy hàm số đã cho đồng biến trên các khoảng \((-\infty;2), (2;+\infty)\).
3. Giải bài 1.3 trang 8 SBT Giải tích 12
Xét tính đơn điệu của các hàm số sau:
|
a) \(y=\dfrac{\sqrt{x}}{x+100}\); |
b) \(y=\dfrac{{{x}^{3}}}{\sqrt{{{x}^{2}}-6}}\). |
Phương pháp giải
- Tìm tập xác định.
- Tính y' và tìm nghiệm của y'=0.
- Xét dấu của y' và kết luận khoảng đồng biến, nghịch biến của hàm số.
Hướng dẫn giải
a) \(y=\dfrac{\sqrt{x}}{x+100} \) . TXĐ: \(\mathbb{R}\backslash \left\{ 2 \right\}\)
\(\begin{align} & y'=\frac{100-x}{2\sqrt{x}{{\left( x+100 \right)}^{2}}} \\ & y'=0\Leftrightarrow x=100 \\ \end{align} \)
Bảng biến thiên:
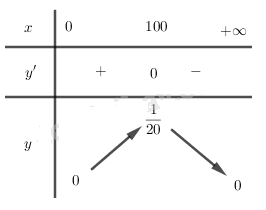
Vậy hàm số đồng biến trên khoảng (0;100) và nghịch biến trên khoảng \(\left( 100;+\infty \right)\)
b) \(y=\dfrac{{{x}^{3}}}{\sqrt{{{x}^{2}}-6}}\) . TXĐ: \((-\infty ;-\sqrt{6})\cup \left( \sqrt{6};+\infty \right)\)
\(\begin{align} & y'=\frac{2{{x}^{2}}\left( {{x}^{2}}-9 \right)}{\left( {{x}^{2}}-6 \right)\sqrt{{{x}^{2}}-6}} \\ & y'=0\Leftrightarrow x=\pm 3 \\ \end{align}\)
Bảng biến thiên:
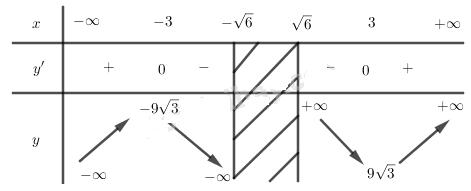
Vậy hàm số đồng biến trên các khoảng \(\left( -\infty ;-3 \right),\left( 3;+\infty \right)\) , nghịch biến trên các khoảng \(\left( -3;-\sqrt{6} \right),\left( \sqrt{6};3 \right)\)
4. Giải bài 1.4 trang 8 SBT Giải tích 12
Xét sự đồng biến, nghịch biến của các hàm số sau:
|
a) \(y=x-\sin x,x\in [0;2\pi]\); |
b) \(y=\sin \dfrac{1}{x}, (x>0)\). |
Phương pháp giải
- Tìm TXĐ.
- Tính y' và xét dấu y'.
- Kết luận.
Hướng dẫn giải
a) \(y=x-\sin x,\,x\in \left[ 0;2\pi \right]\)
\(y'=1-\cos x\ge 0\) với mọi \(x\in \left[ 0;2\pi \right]\)
Dâu “=” xảy ra chỉ tại x=0 và \(x=2\pi\)
Vậy hàm số đồng biến trên đoạn \(\left[ 0;2\pi \right]\)
b) Xét hàm số \(y=\sin \,\dfrac{1}{x}\) với x > 0
\(y'=-\dfrac{1}{{{x}^{2}}}cos\dfrac{1}{x}\)
Giải bất phương trình sau trên khoảng \(\left( 0;+\infty \right)\)
\(\begin{align} & \dfrac{1}{{{x}^{2}}}\left( -cos\dfrac{1}{x} \right)>0\Leftrightarrow cos\dfrac{1}{x}<0 \\ & \Leftrightarrow \dfrac{\pi }{2}\left( 1+4k \right)<\dfrac{1}{x}<\dfrac{\pi }{2}\left( 3+4k \right),\,k=0,1,2... \\ & \Leftrightarrow \dfrac{2}{\pi \left( 1+4k \right)}>x>\dfrac{2}{\pi \left( 3+4k \right)},k=0,1,2... \\ \end{align}\)
Do đó hàm số đồng biến trên các khoảng
\(...,\left( \dfrac{2}{\left( 4k+3 \right)\pi };\dfrac{2}{\left( 4k+1 \right)\pi } \right),\left( \dfrac{2}{\left( 4k-1 \right)\pi };\dfrac{2}{\left( 4k-3 \right)\pi } \right),...,\left( \dfrac{2}{7\pi };\dfrac{2}{5\pi } \right),\left( \dfrac{2}{3\pi };\dfrac{2}{\pi } \right)\)
và nghịch biến trên các khoảng
\(...,\left( \dfrac{2}{\left( 4k+1 \right)\pi };\dfrac{2}{\left( 4k-1 \right)\pi } \right),...,\left( \dfrac{2}{5\pi };\dfrac{2}{3\pi } \right),\left( \dfrac{2}{\pi };+\infty \right)\) với \(k=0,1,2...\)
5. Giải bài 1.5 trang 8 SBT Giải tích 12
Xác định tham số m để hàm số sau:
a) \(y=\dfrac{mx-4}{x-m}\) đồng biến trên từng khoảng xác định;
b) \(y=-x^3+mx^2-3x+4\) nghịch biến trên \((-\infty; +\infty)\).
Phương pháp giải
- Bước 1: Tính y'
- Bước 2: Cho y' > 0 ( y' < 0) để hàm số đồng biến (nghịch biến)
Hướng dẫn giải
a) Tập xác định: \(D=\mathbb{R}\backslash \left\{ m \right\}\)
Hàm số đồng biến trên từng khoảng \(\left( -\infty ;m \right),\left( m;+\infty \right)\) khi và chỉ khi
\(y'=\dfrac{-{{m}^{2}}+4}{{{\left( x-m \right)}^{2}}} > 0\Leftrightarrow -{{m}^{2}}+4 > 0\Leftrightarrow {{m}^{2}} < 4\Leftrightarrow -2 < m < 2 \)
b) Tập xác định: \(D=\mathbb{R}\)
Hàm số nghịch biến trên R khi và chỉ khi
\(\begin{align} & y'=-3{{x}^{2}}+2mx-3\le 0 \\ & \Leftrightarrow \Delta '={{m}^{2}}-9\le 0 \\ & \Leftrightarrow {{m}^{2}}\le 9 \\ & \Leftrightarrow -3\le m\le 3 \\ \end{align}\)
6. Giải bài 1.6 trang 8 SBT Giải tích 12
Chứng minh phương trình sau có nghiệm duy nhất.
\(3(\cos x-1)+2\sin x+6x=0\).
Phương pháp giải
Sử dụng phương pháp hàm số:
- Xét hàm số vế trái và chứng minh nó đơn điệu trên R.
- Từ đó suy ra phương trình có nghiệm duy nhất.
Hướng dẫn giải
Đặt y = 3(cos x – 1) + 2sin x + 6x
Hàm số xác định, liên tục và có đạo hàm tại mọi x ∈ R
Ta có: y(0 ) = 0 và(y' = -3sin x + 2cos x + 6 >0, x ∈ R
Hàm số đồng biến trên R và có một nghiệm x = 0
Vậy phương trình đã cho có một nghiệm duy nhất.
7. Giải bài 1.7 trang 8 SBT Giải tích 12
Chứng minh các bất đẳng thức sau:
a) \(\tan x >\sin x, 0< x< \dfrac{\pi}{2}\);
b) \(1+\dfrac{1}{2}x-\dfrac{x^2}{8}<\sqrt{1+x}<1+\dfrac{1}{2}\,\, \text{với}\,\,x>0\).
Phương pháp giải
a) Xét hàm \(f\left( x \right) = \tan x - \sin x\) và chứng minh nó đồng biến trên \(\left( {0;\dfrac{\pi }{2}} \right)\)
Từ đó suy ra điều phải chứng minh.
b) Xét các hàm số \(f\left( x \right) = 1 + \dfrac{1}{2}x - \dfrac{{{x^2}}}{8} - \sqrt {1 + x}\) và \(g\left( x \right) = \sqrt {1 + x} - 1 - \dfrac{1}{2}x\) trên \(\left( {0; + \infty } \right)\) và chứng minh chúng nghịch biến trên \(\left( {0; + \infty } \right)\)
Từ đó suy ra điều phải chứng minh.
Hướng dẫn giải
a) Xét hàm \(f\left( x \right) = \tan x - \sin x\) trên khoảng \(\left( {0;\dfrac{\pi }{2}} \right)\)ta có:
\(f'\left( x \right) = \dfrac{1}{{{{\cos }^2}x}} - \cos x = \dfrac{{1 - {{\cos }^3}x}}{{{{\cos }^2}x}} > 0\) với \(\forall x \in \left( {0;\dfrac{\pi }{2}} \right)\) vì cos x < 1 với mọi \(x \in \left( {0;\dfrac{\pi }{2}} \right)\) nên \({\cos ^3}x < 1,\forall x \in \left( {0;\dfrac{\pi }{2}} \right)\)
Do đó hàm số \(f\left( x \right) = \tan x - \sin x\) đồng biến trên \(\left( {0;\dfrac{\pi }{2}} \right)\)
\( \Rightarrow f\left( x \right) > f\left( 0 \right) = 0 \Rightarrow \tan x - \sin x > 0 \Leftrightarrow \tan x > \sin x\) với mọi \(x \in \left( {0;\dfrac{\pi }{2}} \right)\)
b)
Xét \(f\left( x \right) = 1 + \dfrac{1}{2}x - \dfrac{{{x^2}}}{8} - \sqrt {1 + x} \) trên \(\left( {0; + \infty } \right)\) ta có: \(f'\left( x \right) = \dfrac{1}{2} - \dfrac{1}{4}x - \dfrac{1}{{2\sqrt {x + 1} }}\)
Vì x > 0 nên \(f'\left( x \right) < \dfrac{1}{2} - \dfrac{1}{4}.0 - \dfrac{1}{{2\sqrt {0 + 1} }} = 0\) nên hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {0; + \infty } \right)\)
Do đó \(f\left( x \right) < f\left( 0 \right) = 0\) \( \Rightarrow 1 + \dfrac{1}{2}x - \dfrac{{{x^2}}}{8} - \sqrt {1 + x} < 0\) \( \Leftrightarrow 1 + \dfrac{1}{2}x - \dfrac{{{x^2}}}{8} < \sqrt {1 + x} \,\,\left( 1 \right)\)
Xét \(g\left( x \right) = \sqrt {1 + x} - 1 - \dfrac{1}{2}x\) trên \(\left( {0; + \infty } \right)\) ta có: \(g'\left( x \right) = \dfrac{1}{{2\sqrt {x + 1} }} - \dfrac{1}{2}\)
Vì x > 0 nên \(g'\left( x \right) < \dfrac{1}{{2\sqrt {0 + 1} }} - \dfrac{1}{2} = 0\) hay \(y = g\left( x \right)\)nghịch biến trên \(\left( {0; + \infty } \right)\)
Do đó \(g\left( x \right) < g\left( 0 \right) = 0\) hay \(\sqrt {1 + x} - 1 - \dfrac{1}{2}x < 0 \Leftrightarrow \sqrt {1 + x} < 1 + \dfrac{1}{2}x\,\,\left( 2 \right)\)
Từ (1) và (2) ta được \(1 + \dfrac{1}{2}x - \dfrac{{{x^2}}}{8} < \sqrt {1 + x} < 1 + \dfrac{1}{2}x\) với x > 0. (đpcm)
8. Giải bài 1.8 trang 8 SBT Giải tích 12
Xác định giá trị của b để hàm số \(f(x)=\sin x-bx+c\) nghịch biến trên toàn trục số.
Phương pháp giải
Hàm số y=f(x) nghịch biến trên D với mọi \(x\in D\) nếu \(f'(x) \le 0,\forall x \in D\)
Hướng dẫn giải
f(x) = sin x - bx + c nghịch biến trên R nếu ta có:
f'(x) = cos x - b \(\le 0,\forall x \in R\)
Vì \(|\cos x| \le 1\) nên \(f'(x) \le 0,\forall x \in R < = > b \ge 1.\)
9. Giải bài 1.9 trang 8 SBT Giải tích 12
Khẳng định nào sau đây đúng?
A. \(y=\sin x\) là hàm số chẵn.
B. Hàm số \(y=\dfrac{\sqrt{3x+5}}{x-1}\) xác định trên \(\mathbb{R}\).
C. Hàm số \(y=x^3+4x-5\) đồng biến trên \(\mathbb{R}\).
D. Hàm số \(y=\sin x+3x-1\) nghịch biến trên \(\mathbb{R}\).
Phương pháp giải
Xét tính đúng sai của mỗi đáp án, sử dụng tính chẵn lẻ, tính đơn điệu của hàm số.
Hướng dẫn giải
Đáp án A sai vì hàm y=sin x là hàm lẻ (do \(sin(-x)=-\sin x\) )
Đáp án B sai vì hàm số \(y=\dfrac{\sqrt{3x+5}}{x-1}\) xác định trên R\{1}.
Đáp án C đúng. Vì \(y'=3{{x}^{2}}+4>0,\,\forall x\in \mathbb{R}\)
Đáp án D sai vì hàm số y=sin x+3x-1 có: y'=cos x+3 > 0, \(\forall x\in \mathbb{R}\) nên hàm số đó đồng biến trên R
Chọn C
10. Giải bài 1.10 trang 8 SBT Giải tích 12
Hàm số \(y=\sqrt{25-x^2}\) nghịch biến trên khoảng:
|
A. \((-\infty;0)\) |
B. \((-5;0)\) |
C. \((0;5)\) |
D. \((5;+\infty)\) |
Phương pháp giải
- Tìm TXĐ D
- Tính y' và tìm nghiệm của y' = 0 trên D.
- Xét dấu y' và suy ra khoảng đồng biến, nghịch biến của hàm số.
Hướng dẫn giải
Đáp án C.
Gợi ý: Loại A, D vì tập xác định của hàm số là \(25-{{x}^{2}}\ge 0\Leftrightarrow -5\le x\le 5\)
Loại B vì:
+ x = -5 thì y = 0
+ x = 0 thì y = 5
Chọn C
11. Giải bài 1.11 trang 9 SBT Giải tích 12
Hàm số \(y=\dfrac{x}{\sqrt{16-x^2}}\) đồng biến trên khoảng:
|
A. \((4;+\infty)\) |
B. \((-4;4)\) |
C. \((-\infty;-4)\) |
D. \(\mathbb{R}\) |
Phương pháp giải
- Tìm TXĐ D
- Tính y' và tìm nghiệm của y' = 0 trên D.
- Xét dấu y' và suy ra khoảng đồng biến, nghịch biến của hàm số.
Hướng dẫn giải
TXĐ: \(D = \left( { - 4;4} \right)\)
Có
\(y' = \dfrac{{\sqrt {16 - {x^2}} - x.\dfrac{{ - 2x}}{{2\sqrt {16 - {x^2}} }}}}{{16 - {x^2}}}\) \( = \dfrac{{\left( {16 - {x^2}} \right) + {x^2}}}{{\left( {16 - {x^2}} \right)\sqrt {16 - {x^2}} }}\) \( = \dfrac{{16}}{{\left( {16 - {x^2}} \right)\sqrt {16 - {x^2}} }} > 0,\) \(\forall x \in \left( { - 4;4} \right)\)
Do đó hàm số đồng biến trên \(\left( { - 4;4} \right)\).
Chọn B.
12. Giải bài 1.12 trang 9 SBT Giải tích 12
Phương trình nào sau đây có nghiệm duy nhất trên \(\mathbb{R}\)?
|
A. \(3\sin^2 x-\cos^2x+5=0\) |
B. \(x^2-5x+6=0\) |
|
C. \(x^5+x^3-7=0\) |
D. \(3\tan x-5=0\) |
Phương pháp giải
Xét tính đơn điệu của mỗi hàm số vế trái, hàm số nào đơn điệu trên \(\mathbb{R}\) thì phương trình có nghiệm duy nhất.
Hướng dẫn giải
Đáp án C vì: Xét hàm \(f\left( x \right) = {x^5} + {x^3} - 7\) có \(f'\left( x \right) = 5{x^4} + 3{x^2} = {x^2}\left( {5{x^2} + 3} \right)\)
\(f'\left( x \right) = 0 \Leftrightarrow x = 0\) và \(f'\left( x \right) \ge 0,\forall x \in \mathbb{R}\) nên hàm số đồng biến trên R
Mặt khác \(f\left( 0 \right) = - 7 < 0,f\left( 2 \right) = 33 > 0\) nên \(f\left( 0 \right).f\left( 2 \right) < 0\)
Hàm số \(y = f\left( x \right)\) liên tục trên [0;2] nên tồn tại \({x_0} \in \left( {0;2} \right)\) để x0 = 0 hay phương trình f( x ) = 0 có nghiệm duy nhất trên R
Chọn C.
13. Giải bài 1.13 trang 9 SBT Giải tích 12
Phương trình nào sau đây có nghiệm duy nhất trên \(\mathbb{R}\)?
|
A. \(x^2-7x+12=0\) |
B. \(x^3+5x+6=0\) |
|
C. \(x^4-3x^2+1=0\) |
D. \(2\sin x\cos^2x-2\sin x-\cos^2x+1=0\) |
Phương pháp giải
Xét tính đơn điệu của mỗi hàm số vế trái, hàm số nào đơn điệu trên R thì phương trình có nghiệm duy nhất.
Hướng dẫn giải
Đáp án B vì: Xét hàm \(f\left( x \right) = {x^3} + 5x + 6\) có \(f'\left( x \right) = 3{x^2} + 5 > 0,\forall x \in \mathbb{R}\) nên hàm số đồng biến trên R
Mặt khác, f( - 1) = 0 nên phương trình f( x ) = 0 có nghiệm duy nhất trên R
Chọn B.
14. Giải bài 1.14 trang 9 SBT Giải tích 12
Phương trình nào sau đây có nghiệm duy nhất trên \(\mathbb{R}\)?
|
A. \((x-5)(x^2-x-12)=0\) |
B. \(-x^3+x^2-3x+2=0\) |
|
C. \(\sin^2x-5\sin x+4=0\) |
D. \(\sin x-\cos x+1=0\) |
Phương pháp giải
Loại đáp án, xét các đáp án bằng cách giải mỗi phương trình và suy ra số nghiệm.
Hướng dẫn giải
Đáp án B.
Các phương trình còn lại có nhiều hơn một nghiệm:
\(\left( x-5 \right)\left( {{x}^{2}}-x-12 \right)=0\) có các nghiệm là x=5; 4; -3
\(\sin {{\,}^{2}}x-5\sin x+4=0\Leftrightarrow \sin x=1\), có vô số nghiệm
\(\sin \,x-\cos x+1=0\) có các nghiệm \(x=0;x=\dfrac{3\pi }{2}\)
15. Giải bài 1.15 trang 9 SBT Giải tích 12
Tìm giá trị của tham số m để hàm số \(y=x^3-2mx^2+12x-7\) đồng biến trên \(\mathbb{R}\).
|
A. \(m=4\) |
B. \(m\in (0;+\infty)\) |
|
C. \(m\in (-\infty;0)\) |
D. \(-3\le x\le 3\). |
Phương pháp giải
- Tính y'
- Hàm số đồng biến trên \(\mathbb{R} \Leftrightarrow y' \ge 0,\forall x \in \mathbb{R}\)
Hướng dẫn giải
TXĐ: D = R
Ta có: \(y' = 3{x^2} - 4mx + 12\)
Hàm số đồng biến trên \(\mathbb{R} \Leftrightarrow y' \ge 0,\forall x \in \mathbb{R} \Leftrightarrow 3{x^2} - 4mx + 12 \ge 0,\forall x \in \mathbb{R}\)
\(\Leftrightarrow \Delta ' = 4{m^2} - 36 \le 0 \Leftrightarrow {m^2} \le 9\) \( \Leftrightarrow - 3 \le m \le 3\)
Chọn D.
16. Giải bài 1.16 trang 9 SBT Giải tích 12
Tìm giá trị của tham số m để hàm số \(y=\dfrac{-mx-5m+4}{x+m}\) nghịch biến trên từng khoảng xác định.
|
A. \(m < 1\) hoặc \(m >4\) |
B. \(0 < m < 1\) |
|
C. \(m >4\) |
D. \(1\le m\le 4\) |
Phương pháp giải
- Tính y'
- Hàm số nghịch biến trên từng khoảng xác định nếu y' < 0 trên từng khoảng xác định.
Hướng dẫn giải
Đáp án A. Hàm số xác định trên R \ {-m}
Hàm số nghịch biến trên từng khoảng \(\left( -\infty ;-m \right),\left( -m;+\infty \right)\) khi và chỉ khi
\(\begin{aligned} & y'=\dfrac{-{{m}^{2}}+5m-4}{{{\left( x+m \right)}^{2}}} < 0 \\ & \Leftrightarrow -{{m}^{2}}+5m-4 < 0 \\ & \Leftrightarrow \left[ \begin{aligned} & m < 1 \\ & m > 4 \\ \end{aligned} \right. \\ \end{aligned}\)
Chọn A
Các em hãy luyện tập bài trắc nghiệm Sự đồng biến, nghịch biến của hàm số Toán 12 sau để nắm rõ thêm kiến thức bài học.
Tham khảo thêm
- doc Giải bài tập SBT Toán 12 Bài 2: Cực trị của hàm số
- doc Giải bài tập SBT Toán 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- doc Giải bài tập SBT Toán 12 Bài 4: Đường tiệm cận
- doc Giải bài tập SBT Toán 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số