Giải bài tập SBT Toán 12 Bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Giải bài tập SBT Toán 12 Bài Khảo sát sự biến thiên và vẽ đồ thị của hàm số giúp các em học sinh sẽ dễ dàng ôn tập lại các kiến thức đã học, rèn luyện khả năng tính toán nhanh và chính xác. Sau đây mời các em cùng tham khảo lời giải tương ứng với từng bài tập SGK.
Mục lục nội dung
1. Giải bài 1.56 trang 36 SBT Giải tích 12
2. Giải bài 1.57 trang 36 SBT Giải tích 12
3. Giải bài 1.58 trang 36 SBT Giải tích 12
4. Giải bài 1.59 trang 36 SBT Giải tích 12
5. Giải bài 1.60 trang 36 SBT Giải tích 12
6. Giải bài 1.61 trang 36 SBT Giải tích 12
7. Giải bài 1.62 trang 37 SBT Giải tích 12
8. Giải bài 1.63 trang 37 SBT Giải tích 12
9. Giải bài 1.64 trang 38 SBT Giải tích 12
10. Giải bài 1.65 trang 38 SBT Giải tích 12
11. Giải bài 1.66 trang 38 SBT Giải tích 12
12. Giải bài 1.67 trang 38 SBT Giải tích 12
13. Giải bài 1.68 trang 38 SBT Giải tích 12
14. Giải bài 1.69 trang 38 SBT Giải tích 12
15. Giải bài 1.70 trang 38 SBT Giải tích 12
16. Giải bài 1.71 trang 39 SBT Giải tích 12
17. Giải bài 1.72 trang 39 SBT Giải tích 12

1. Giải bài 1.56 trang 36 SBT Giải tích 12
Khảo sát và vẽ đồ thị các hàm số:
\(a)\,y=2-3x-x^2;\\ b)\,y=x^3-x^2+x;\\ c)\,y=-x^4+2x^3+3\)
Phương pháp giải
- Tìm TXĐ.
- Xét sự biến thiên.
+ Tìm các giới hạn tại vô cực.
+ Tìm khoảng đồng biến, nghịch biến.
+ Tìm cực trị (nếu có).
+ Lập bảng biến thiên.
- Vẽ đồ thị hàm số.
Hướng dẫn giải
a)
\(y=2-3x-x^2=-x^2-3x+2\)
TXĐ: \(D=\mathbb R\)
\(y'=-2x-3\\ y'=0\Leftrightarrow x=-\dfrac 3 2\)
Hàm số đồng biến trên khoảng \(\left(-\infty;-\dfrac 3 2\right)\) và nghịch biến trên khoảng \(\left(-\dfrac 3 2;+\infty\right)\)
\(\lim\limits_{x\to{-\infty}}y=\lim\limits_{x\to{+\infty}}y=-\infty\)
Hàm số đạt cực đại tại \(x=-\dfrac 3 2; y=\dfrac{17} 4\)
Bảng biến thiên:
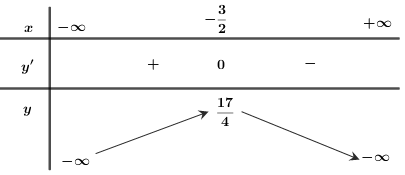
Đồ thị hàm số:
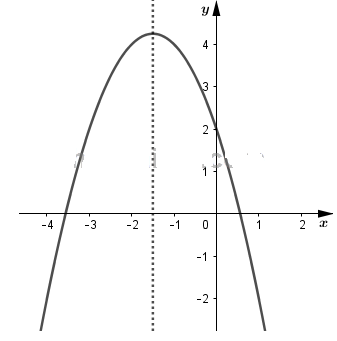
b)
TXĐ: \(D=\mathbb R\)
\(y'=3x^2-2x+1\\ y'=2x^2+(x-1)^2>0\forall x\)
Hàm số luôn đồng biến trên \(\mathbb R\)
\(\lim\limits_{x\to{-\infty}}y=-\infty;\,\lim\limits_{x\to{+\infty}}y=+\infty\)
Hàm số không có cực trị
Bảng biến thiên:
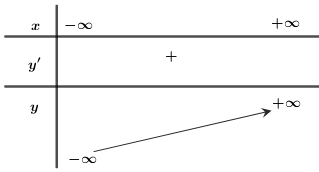
Đồ thị hàm số:
.png)
c)
TXĐ: \(D=\mathbb R\)
\(y'=-4x^3+6x^2\\ y'=0\Leftrightarrow \left[\begin{align}&x=0\\ &x=\dfrac 3 2\\ \end{align}\right.\)
Hàm số đồng biến trên các khoảng \((-\infty;\dfrac{3}{2})\) và nghịch biến trên khoảng \((\dfrac{3}{2};+\infty)\)
\(\lim\limits_{x\to{-\infty}}y=\lim\limits_{x\to{+\infty}}y=-\infty\)
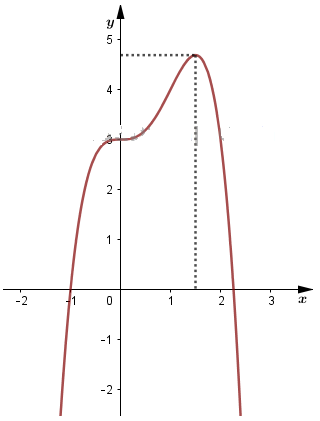
Hàm số đạt cực đại tại \(x=\dfrac 3 2;y\left(\dfrac 3 2\right)=\dfrac{75}{16}\)
Bảng biến thiên:
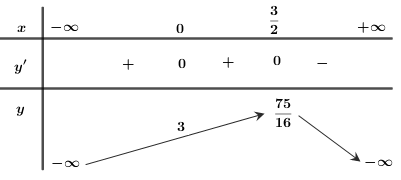
Đồ thị hàm số:
2. Giải bài 1.57 trang 36 SBT Giải tích 12
Khảo sát và vẽ đồ thị các hàm số :
\(a)\,y=\dfrac{x-2}{x+1};\\b)\,y=\dfrac{2-x}{2x-1}.\)
Phương pháp giải
* Tìm TXĐ.
* Xét sự biến thiên:
+ Tính \(y'\).
+ Tìm khoảng đồng biến, nghịch biến.
+ Tìm các đường tiệm cận.
+ Lập bảng biến thiên.
* Vẽ đồ thị hàm số.
Hướng dẫn giải
a) Tập xác định \(D=\mathbb{R}\backslash \left\{ -1 \right\}\)
\(y'=\dfrac 3 {(x+1)^2}>0\,\,\forall x\in D\)
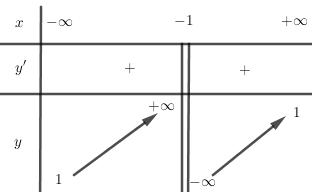
Hàm số đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(-1; +\infty\right)\)
\(\lim\limits_{x\to -\infty}y=\lim\limits_{x\to +\infty}y=1\). Tiệm cận ngang của đồ thị hàm số là đường thẳng \(y=1\)
\(\lim\limits_{x\to -1^-}y=+\infty; \lim\limits_{x\to -1^+}y=-\infty.\)Tiệm cận đứng của đồ thị hàm số là đường thẳng \(x=-1\)
Đồ thị hàm số không có cực trị
Bảng biến thiên
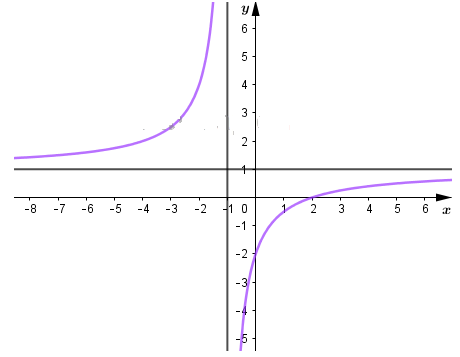
Đồ thị hàm số
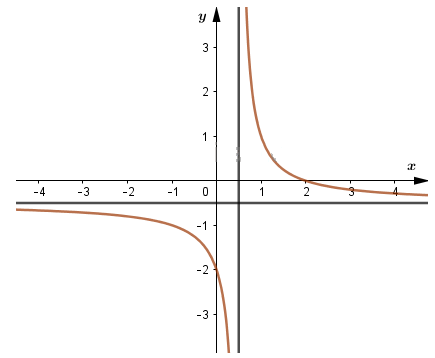
b) \(y=\dfrac{2-x}{2x-1}=\dfrac{-x+2}{2x-1}\)
Tập xác định \(D=\mathbb{R}\backslash \left\{ -\dfrac 1 2 \right\}\)
\(y'=\dfrac {-3} {(2x+1)^2}<0\,\,\forall x\in D\)
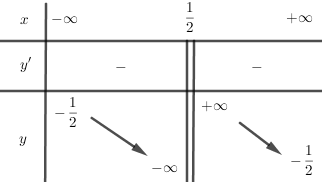
Hàm số nghịch biến trên các khoảng \(\left(-\infty;-\dfrac 1 2\right)\) và \(\left(-\dfrac 1 2; +\infty\right)\)
\(\lim\limits_{x\to -\infty}y=\lim\limits_{x\to +\infty}y=-\dfrac 1 2\). Tiệm cận ngang của đồ thị hàm số là đường thẳng \(y=-\dfrac 1 2\)
\(\lim\limits_{x\to {\frac{-1} 2}^-}y=-\infty; \lim\limits_{x\to {\frac{-1} 2}^+}y=+\infty.\)Tiệm cận đứng của đồ thị hàm số là đường thẳng \(x=-\dfrac1 2\)
Đồ thị hàm số không có cực trị
Bảng biến thiên
Đồ thị hàm số
3. Giải bài 1.58 trang 36 SBT Giải tích 12
Tìm giá trị của tham số m để hàm số
a) \(y=x^3+(m+3)x^2+mx-2\) đạt cực tiểu tại \(x=1\)
b) \(y=-\dfrac 1 3 (m^2+6m)x^3-2mx^2+3x+1\) đạt cực đại tại \(x=-1\)
Phương pháp giải
Sử dụng phương pháp điều kiện cần, điều kiện đủ.
- Sử dụng điều kiện x = x0 là điểm cực trị của hàm số thì \(f'\left( {{x_0}} \right) = 0\) tìm m.
- Thay m tìm được ở trên vào hàm số và kiểm tra x = x0 có là điểm cực trị theo yêu cầu hay không.
Hướng dẫn giải
a)
Ta có:
\(y'=3x^2+2(m+3)x+m\)
\(y''=6x+2(m+3)\)
Hàm số đạt cực tiểu tại \(x=1\) khi:
\(\left\{ \begin{aligned} & y'(1)=0 \\ & y''(1)>0 \\ \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned} & 3+2(m+3)+m=0 \\ & 6+2(m+3)>0 \\ \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned} & m=-3 \\ & m>-6 \\ \end{aligned} \right. \)
Vậy \(m=-3\)
b)
\(y'=-(m^2+6m)x^2-4mx+3\\ y''=-2(m^2+6m)x-4m\)
Hàm số đạt cực đại tại \(x=-1\) khi :
\(\left\{ \begin{aligned} & y'(-1)=0 \\ & y''(-1)<0 \\ \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned} & -(m^2+6m)+4m+3=0 \\ & 2(m^2+6m)-4m<0 \\ \end{aligned} \right.\Leftrightarrow \left\{ \begin{aligned} & \left[ \begin{aligned} & m=1 \\ & m=-3 \\ \end{aligned} \right. \\ & -4 < m<0 \\ \end{aligned} \right.\Rightarrow m=-3 \)
Vậy \(m=-3\)
4. Giải bài 1.59 trang 36 SBT Giải tích 12
Tìm giá trị của tham số m để hàm số
\(y=(m-1)x^4-mx^2+3\) có đúng một cực trị
Phương pháp giải
- Tính y'.
- Điều kiện để hàm số đã cho có đúng một cực trị là phương trình y' = 0 có nghiệm duy nhất x = 0.
Hướng dẫn giải
Ta có:
\(y'=4(m-1)x^3-2mx=x[4(m-1)x^2-2m]\)
Với \(m =1\), ta có: \(y'=-2x\Rightarrow y'=0\Leftrightarrow x=0\)
Với \(m\ne 1\)
\(y'=0\Leftrightarrow \left[ \begin{aligned} & x=0 \\ & x^2=\dfrac{2m}{4(m-1)} \,\,\,(*)\\ \end{aligned} \right. \)
Để hàm số có đúng một cực trị, thì phương trình \(y'=0\) có một nghiệm duy nhất.
Hay phương trình (*) vô nghiệm hoặc có 1 nghiệm duy nhất bằng 0
\(\Rightarrow \dfrac{2m}{4(m-1)}\le0\\ \Leftrightarrow 0\le m < 1\)
Vậy \(0\le m\le 1\)
5. Giải bài 1.60 trang 36 SBT Giải tích 12
Cho hàm số \(y=\dfrac 1 4 x^3-\dfrac 3 2 x^2+5\)
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho;
b) Tìm các giá trị của tham số m để phương trình \(x^3-6x^2+m=0\) có ba nghiệm phân biệt
Phương pháp giải
- Tìm TXĐ.
- Xét sự biến thiên.
+ Tìm các giới hạn tại vô cực.
+ Tìm khoảng đồng biến, nghịch biến.
+ Tìm cực trị (nếu có).
+ Lập bảng biến thiên.
- Vẽ đồ thị hàm số.
Hướng dẫn giải
a)
TXĐ: \(D=\mathbb R\)
\(y'=\dfrac 3 4 x^2-3x\\ y'=0\Leftrightarrow \left[ \begin{aligned} & x=0 \\ & x=4 \\ \end{aligned} \right. \)
\(\lim\limits_{x\to-\infty}y=-\infty;\lim\limits_{x\to+\infty}y=+\infty\)
Bảng biến thiên
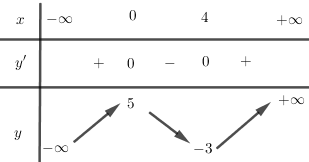
Đồ thị hàm số không có tiệm cận, đạt cực đại tại \(x=0,y(0)=5\) và đạt cực tiểu tại \(x=4, y(4)=-3\)
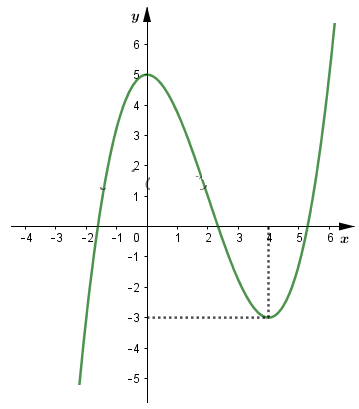
Đồ thị (C)
b)
Ta có:
\(x^3-6x^2+m=0\\ \Leftrightarrow\dfrac {1}{4}x^3-\dfrac{3}{2}x^2+5=\dfrac {-m} 4+5\,\,\,\,(*)\)
Số nghiệm của phương trình (*) là số giao điểm của đường thẳng \(y=-\dfrac m 4 +5\) và đồ thị (C).
Từ đồ thị hàm số, ta có:
Nếu \(\left\{ \begin{aligned} & -\dfrac{m}{4}+5<5 \\ & -\dfrac{m}{4}+5>-3 \\ \end{aligned} \right.\Leftrightarrow 0< m<32\) thì phương trình (*) có ba nghiệm phân biệt.
6. Giải bài 1.61 trang 36 SBT Giải tích 12
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
\(y=-x^3+3x+1\)
b) Chỉ ra phép biến hình biến (C) thành đồ thị (C') của hàm số
\(y=(x+1)^3-3x-4\)
c) Dựa vào đồ thị (C'), biện luận theo m số nghiệm của phương trình
\((x+1)^3=3x+m\)
d) Viết phương trình tiếp tuyến (d) của đồ thị (C'), biết tiếp tuyến vuông góc với đường thẳng \(y=-\dfrac x 9+1\)
Phương pháp giải
- Tìm TXĐ.
- Xét sự biến thiên.
+ Tìm các giới hạn tại vô cực.
+ Tìm khoảng đồng biến, nghịch biến.
+ Tìm cực trị (nếu có).
+ Lập bảng biến thiên.
- Vẽ đồ thị hàm số.
Hướng dẫn giải
a)
TXĐ: \(D=\mathbb R\)
\(y'=-3x^2+3\\ y'=0\Leftrightarrow x=\pm 1 \)
\(\lim\limits_{x\to -\infty}y=+\infty;\,\,\lim\limits_{x\to +\infty}y=-\infty;\)
Bảng biến thiên:
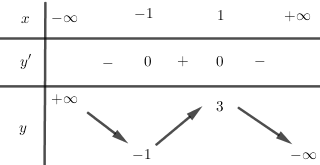
Hàm số đồng biến trên khoảng \((-1;1)\) và nghịch biến trên các khoảng \((-\infty;-1);(1;+\infty)\)
Hàm số đạt cực tiểu tại \((-1;-1)\); đạt cực đại tại \((1;3)\)
Đồ thị
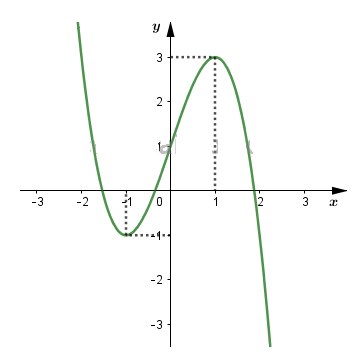
b)
Ta có:
\(y=(x+1)^3-3x-4=(x+1)^3-3(x+1)-1=-[-(x+1)^3+3x+1]\)
Vậy ta thực hiện liên tiếp các phép biến hình để thu được đồ thị (C')
- Tịnh tiến đồ thị (C) song song với trục Ox sang trái 1 đơn vị được đồ thị (\(C_1\))
- Lấy đối xứng đồ thị (\(C_1\)) qua Ox được đồ thị (C')
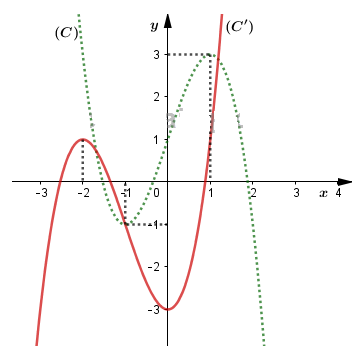
c) Ta có:
\((x+1)^3=3x+m\Leftrightarrow (x+1)^3-3x-4=m-4\)
Từ đồ thị ta có:
+) Nếu \(\left[ \begin{aligned} & m-4>1 \\ & m-4<-3 \\ \end{aligned} \right.\Leftrightarrow \left[ \begin{aligned} & m>5 \\ & m<1 \\ \end{aligned} \right.\) phương trình có 1 nghiệm
+) Nếu \(\left\{ \begin{aligned} & m-4>-3 \\ & m-4<1 \\ \end{aligned} \right.\Leftrightarrow 1< m<5\) phương trình có 3 nghiệm phân biệt
+) Nếu \( \left[ \begin{aligned} & m-4=-3 \\ & m-4=1 \\ \end{aligned} \right.\Leftrightarrow \left[ \begin{aligned} & m=1 \\ & m=5 \\ \end{aligned} \right.\) phương trình có 2 nghiệm phân biệt
d)
\(y'=3(x+1)^2-3\)
Gọi \(M(x_0;y_0)\) là tiếp điểm của tiếp tuyến với đồ thị (C')
Ta lại có tiếp tuyến vuông góc với đường thẳng \(y=-\dfrac x 9+1\)
\(y'(x_0)=9\Rightarrow 3(x_0+1)^2-3=9\Leftrightarrow \left[ \begin{aligned} & x_0=1 \\ & x_0=-3 \\ \end{aligned} \right. \)
Vậy có hai tiếp điểm thỏa mãn \((1;1)\) và \((-3;-3)\)
Nên phương trình tiếp tuyến có dạng: \(y=9x-8\) hoặc \(y=9x+24\)
7. Giải bài 1.62 trang 37 SBT Giải tích 12
Biện luận theo k số nghiệm của phương trình
\(a)\,(x-1)^2=2|x-k|;\\ b)\,(x+1)^2(2-x)=k\)
Phương pháp giải
a)
- Phá dấu giá trị tuyệt đối đưa về hai phương trình mới.
- Biến đổi các phương trình về dạng \(f\left( x \right) = g\left( k \right)\)
- Vẽ đồ thị các hàm số y = f(x) trên cùng một hệ trục tọa độ.
- Từ đó biện luận nghiệm của phương trình, sử dụng sự tương giao giữa đường thẳng y = g(k) với đồ thị hàm số \(y = f\left( x \right)\)
b)
- Khảo sát và vẽ đồ thị hàm số \(y = {\left( {x + 1} \right)^2}\left( {2 - x} \right)\)
- Biện luận số nghiệm dựa vào tương giao đồ thị.
Hướng dẫn giải
a)
Phương trình đã cho tương đương với
\(\begin{aligned} & 2\left( x-k \right)=\pm {{\left( x-1 \right)}^{2}} \\ & \Leftrightarrow \left[ \begin{aligned} & -{{x}^{2}}+4x-1=2k \\ & {{x}^{2}}+1=2k \\ \end{aligned} \right. \\ \end{aligned}\)
Vẽ đồ thị hai hàm số \(y=-{{x}^{2}}+4x-1 \,\,\text{và}\,\, y={{x}^{2}}+1 \)
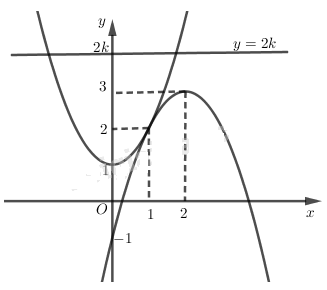
Từ đồ thị, ta có:
\(2k>3\): Phương trình có hai nghiệm
\(2k=3\): Phương trình có ba nghiệm
\(2<2k<3\): Phương trình có 4 nghiệm
\(2k=2\): Phương trình có 3 nghiệm
\(1<2k<2\): Phương trình có 4 nghiệm
\(2k=1\): Phương trình có 3 nghiệm
\(2k<1\): Phương trình có 2 nghiệm
Vậy
\(1< k<\dfrac{3}{2}\) hoặc \(\dfrac{1}{2}< k<1\): phương trình có bốn nghiệm
\(k=1\) hoặc \(k=\dfrac 1 2\) hoặc \(k=\dfrac 3 2\): phương trình có ba nghiệm
\(k>\dfrac{3}{2}\) hoặc \(k<\dfrac{1}{2}\) : phương trình có ba nghiệm
b)
Ta có:
\({{\left( x+1 \right)}^{2}}\left( 2-x \right)=-{{x}^{3}}=3x+2 \)
Vẽ đồ thị hàm số \( y=-{{x}^{3}}+3x+2\)
Ta vẽ được đồ thị hàm số:
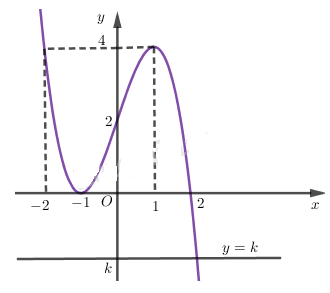
Từ đồ thị hàm số ta có:
\(k>4\) hoặc \(k<0\): phương trình có một nghiệm
\(k=4\) hoặc \(k=0\): phương trình có hai nghiệm
\(0< k<4\) phương trình có ba nghiệm
8. Giải bài 1.63 trang 37 SBT Giải tích 12
Cho hàm số
\(y=x^3-(m+4)x^2-4x+m\,\,\,\,\,\,(1)\)
a) Tìm các điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của m.
b) Chứng minh rằng với mọi giá trị của m, đồ thị của hàm số (1) luôn luôn có cực trị.
c) Khảo sát sự biến thiên và vẽ đồ thị (C) của (1) khi \(m = 0\).
d) Xác định \(k\) để (C) cắt đường thẳng \(y=kx\) tại ba điểm phân biệt
Phương pháp giải
a)
- Biến đổi hàm số về phương trình ẩn m với tham số là x,y
- Cho các hệ số của m và hệ số tự do bằng 0 rồi tìm x, y và kết luận.
b) Hàm số đa thức bậc ba luôn có cực trị nếu y' = 0 luôn có hai nghiệm phân biệt với \(\forall m\)
c)
Khảo sát tóm tắt:
+ Thay m = 0 vào hàm số đã cho.
+ Tính y'.
+ Lập bảng biến thiên và vẽ đồ thị hàm số.
d)
- Giải phương trình hoành độ giao điểm tìm nghiệm đặc biệt.
- Từ đó suy ra điều kiện của k
Hướng dẫn giải
a)
Gọi \((x_0;y_0)\) là điểm cố định mà đồ thị hàm số luôn đi qua với mọi m
\(y_0=x_0^3-(m+4)x_0^2-4x_0+m\\ \Leftrightarrow x_0^3-mx_0^2-4x_0^2-4x_0+m-y_0=0\\ \Leftrightarrow (x_0^3-4x_0^2-4x_0-y_0)-m(x_0^2-1)=0\,\,\,(*)\)
Vì \((x_0;y_0)\) cố định, nên ta có phương trình (*) đúng với mọi m, ta có:
\(\begin{aligned} & \left\{ \begin{aligned} & x_{0}^{3}-4x_{0}^{2}-4{{x}_{0}}-{{y}_{0}}=0 \\ & x_{0}^{2}-1=0 \\ \end{aligned} \right. \\ & \Leftrightarrow \left[ \begin{aligned} & \left\{ \begin{aligned} & {{x}_{0}}=1 \\ & {{y}_{0}}=-7 \\ \end{aligned} \right. \\ & \left\{ \begin{aligned} & {{x}_{0}}=-1 \\ & {{y}_{0}}=-1 \\ \end{aligned} \right. \\ \end{aligned} \right. \\ \end{aligned} \)
Vậy có hai điểm cố định mà đồ thị hàm số luôn đi qua là \((1;-7)\) và \((-1;-1)\)
b) Ta có:
\(y'=3x^2-2(m+4)x-4\)
\(\Delta'=(m+4)^2+12>0\,\,\forall m\)
Vậy đồ thị hàm số (1) luôn có cực trị.
c) Với \(m=0\) ta có:
\(y=x^3-4x^2-4x\)
TXĐ: \(D=\mathbb R\)
\(y'=3x^2-8x-4\)
\(\lim\limits_{x\to-\infty}y=-\infty; \lim\limits_{x\to+\infty}y=+\infty\)
Đồ thị
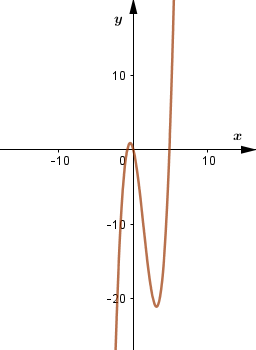
d)
Xét phương trình hoành độ giao điểm
\(x^3-4x^2-4x=kx\\ \Leftrightarrow x^3-4x^2-(4+k)x=0\\ \Leftrightarrow \left[ \begin{aligned} & x=0 \\ & x^2-4x-4-k=0\,\,\,(*) \\ \end{aligned} \right. \)
Để (C) cắt đường thẳng \(y=kx\) tại ba điểm phân biệt thì phương trình (*) có hai nghiệm phân biệt khác 0, hay:
\(\left\{ \begin{aligned} & 4+4+k>0 \\ & k\ne -4 \\ \end{aligned} \right. \Leftrightarrow \left\{ \begin{aligned} & k >-8 \\ & k\ne -4 \\ \end{aligned} \right. \)
9. Giải bài 1.64 trang 38 SBT Giải tích 12
Cho hàm số y = 2x4 − 4x2 (1)
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1).
b) Với giá trị nào của m, phương trình x2|x2 − 2| = m có đúng 6 nghiệm thực phân biệt?
Phương pháp giải
a) - Tìm TXĐ.
- Xét sự biến thiên.
- Vẽ đồ thị hàm số.
b)
- Biến đổi phương trình đã cho về \(\left| {2{x^4} - 4{x^2}} \right| = 2m\)
- Dựng đồ thị hàm số \(y = \left| {2{x^4} - 4{x^2}} \right|\) từ đồ thị hàm số đã vẽ ở ý a:
+ Giữ nguyên phần đồ thị phía trên trục Ox.
+ Lấy đối xứng phần dưới qua Ox và xóa phần dưới đi.
- Biện luận số nghiệm dựa vào số giao điểm của đường thẳng y = 2m và đồ thị vừa vẽ được.
Hướng dẫn giải
a)
Tập xác định: D = R
\(y' = 8{x^3} - 8x = 8x({x^2} - 1)\); \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 0\\x = 1\end{array} \right.\)
Hàm số đồng biến trên mỗi khoảng \(\left( { - 1;0} \right) và \left( {1; + \infty } \right)\)
Hàm số nghịch biến trên mỗi khoảng \(\left( { - \infty ; - 1} \right) và \left( {0;1} \right)\)
Hàm số đạt cực đại tại \(x = 0;{y_{CD}} = 0\)
Hàm số đạt cực tiểu tại \(x = \pm 1;{y_{CT}} = - 2\)
Giới hạn: \(\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty\)
\(y'' = 24{x^2} - 8;\)\(y'' = 0 \Leftrightarrow {x^2} = \dfrac{1}{3} \Leftrightarrow x = \pm \dfrac{{\sqrt 3 }}{3}\)
Đồ thị có hai điểm uốn: \({I_1}\left( { - \dfrac{{\sqrt 3 }}{3}; - \dfrac{{10}}{9}} \right);{I_2}\left( {\dfrac{{\sqrt 3 }}{3}; - \dfrac{{10}}{9}} \right)\)
Bảng biến thiên:
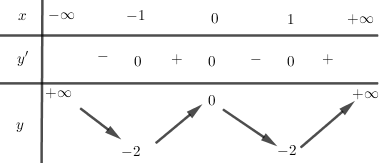
Đồ thị:
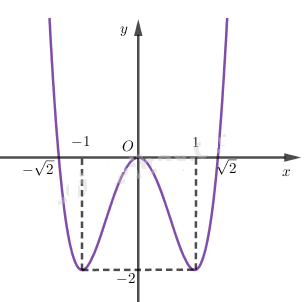
Đồ thị cắt trục hoành tại: \(A( - \sqrt 2 ;0),O(0;0),B(\sqrt 2 ;0)\)
b)
Ta có:
\({x^2}|{x^2} - 2| = m\)\( \Leftrightarrow 2{x^2}\left| {{x^2} - 2} \right| = 2m\)\( \Leftrightarrow \left| {2{x^2}\left( {{x^2} - 2} \right)} \right| = 2m\)\( \Leftrightarrow \left| {2{x^4} - 4{x^2}} \right| = 2m\)
Từ đồ thị hàm số \(y = 2{x^4}-4{x^2}\) có thể suy ra đồ thị của hàm số \(y = \left| {2{x^4} - 4{x^2}} \right|\) như sau:
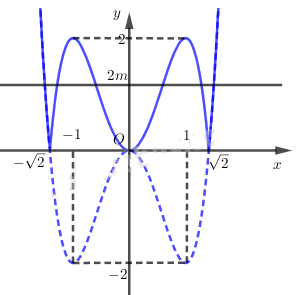
Phương trình: \(\left| {2{x^4} - 4{x^2}} \right| = 2m\) có 6 nghiệm phân biệt khi và chỉ khi đường thẳng y = 2m giao với đồ thị trên tại 6 điểm phân biệt
\(\Leftrightarrow 0 < 2m < 2\) \( \Leftrightarrow 0 < m < 1\)
Vậy 0 < m < 1.
10. Giải bài 1.65 trang 38 SBT Giải tích 12
Cho hàm số:
\(y = \dfrac{{{x^4}}}{4} - 2{x^2} - \dfrac{9}{4}\)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Viết phương trình tiếp tuyến của (C) tại các giao điểm của nó với trục Ox.
c) Biện luận theo k số giao điểm của (C) với đồ thị (P) của hàm số: y = k – 2x2.
Phương pháp giải
a) Khảo sát tóm tắt:
- Tìm TXĐ, tính đạo hàm y'.
- Lập bảng biến thiên và vẽ đồ thị hàm số.
b)
- Giải phương trình hoành độ giao điểm.
- Tìm tọa độ giao điểm của (C) với Ox
- Viết phương trình tiếp tuyến theo công thức \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\)
c)
- Xét phương trình hoành độ giao điểm.
- Biện luận số giao điểm theo số nghiệm của phương trình và kết luận.
Hướng dẫn giải
a) Tập xác định: D = R
Có
\(y' = {x^3} - 4x;\) \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 2\end{array} \right.\)
Bảng biến thiên:
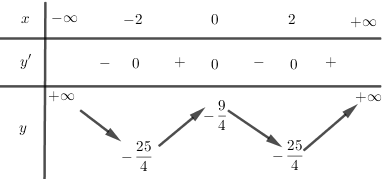
Đồ thị:
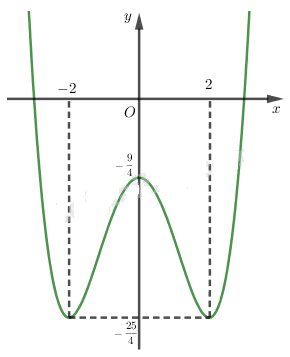
b) \(y = \dfrac{{{x^4}}}{4} - 2{x^2} - \dfrac{9}{4}\)
⇔ x4 − 8x2 − 9 = 0
⇔ (x2 + 1)(x2 − 9) = 0
⇔ \(\left[ \begin{array}{l} x = - 3\\ x = 3 \end{array} \right.\)
(C) cắt trục Ox tại x = -3 và x = 3
Ta có: y′ = x3 − 4x
Phương trình tiếp tuyến của (C) tại điểm có hoành độ x = 3 và x = -3 lần lượt là:
y = y′(3)(x – 3) và y = y′(−3)(x + 3)
Hay y = 15(x – 3) và y = −15(x + 3)
c)
\(\dfrac{{{x^4}}}{4} - 2{x^2} - \dfrac{9}{4} = k - 2{x^2}\)\( \Leftrightarrow {x^4} = 9 + 4k\,\,\left( * \right)\)
Từ đó, ta có:
k = \(-\dfrac{9}{4}\): (C) và (P) có một điểm chung là (0; −9/4)
k > \(-\dfrac{9}{4}\): (C) và (P) có hai giao điểm.
k < \(-\dfrac{9}{4}\): (C) và (P) không cắt nhau.
11. Giải bài 1.66 trang 38 SBT Giải tích 12
Cho hàm số \(y=\dfrac{2x+1}{x-2}\)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Viết phương trình tiếp tuyến của đồ thị (C), biết hệ số góc của tiếp tuyến bằng -5.
Phương pháp giải
a)
- Tìm TXĐ.
- Xét sự biến thiên.
- Vẽ đồ thị hàm số.
b)
- Giải phương trình y' = k tìm hoành độ giao điểm.
- Viết phương trình tiếp tuyến theo công thức \(y = k\left( {x - {x_0}} \right) + {y_0}\)
Hướng dẫn giải
a)
TXĐ: \( D=\mathbb{R}\backslash \left\{ 2 \right\}\)
\(\lim\limits_{x\to\pm \infty}\,\dfrac{2x+1}{x-2}=2\) nên tiệm cận ngang của đồ thị là \(y=2\)
\(\lim\limits_{x\to2^-}\,y=-\infty; \lim\limits_{x\to2^+}\,y=+\infty\) nên tiệm cận đứng của đồ thị là \( x=2\)
\(y'=\dfrac{-5}{{{\left( x-2 \right)}^{2}}}<0\,\,\forall x\in D \)
Vậy hàm số nghịch biến trên \(\left( -\infty ;2 \right);\,\,\left( 2;+\infty \right) \)
Bảng biến thiên
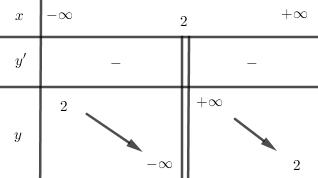
Đồ thị
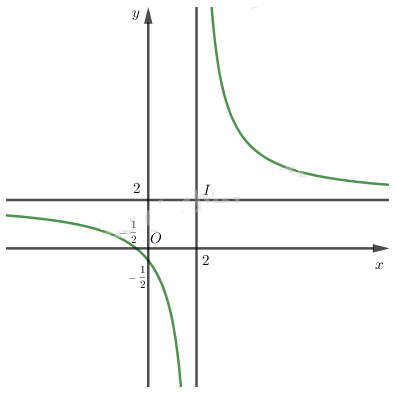
b)
Ta có:
\(y'=\dfrac{-5}{{{\left( x-2 \right)}^{2}}} \)
Gọi tiếp điểm của tiếp điểm và đồ thị là \(\left( {{x}_{0}};{{y}_{0}} \right) \)
Vì tiếp tuyến có hệ số góc là \(-5\) nên ta có:
\(\dfrac{-5}{{{\left( {{x}_{0}}-2 \right)}^{2}}}=-5\Rightarrow {{\left( {{x}_{0}}-2 \right)}^{2}}=1\Leftrightarrow \left[ \begin{align} & {{x}_{0}}=1\Rightarrow {{y}_{0}}=-3 \\ & {{x}_{0}}=3\Rightarrow {{y}_{0}}=7 \\ \end{align} \right.\)
Từ đó ta có hai phương trình tiếp tuyến phải tìm là
\(\begin{align} & y+3=-5\left( x-1 \right)\Leftrightarrow y=-5x+2 \\ & y-7=-5\left( x-3 \right)\Leftrightarrow y=-5x+22 \\ \end{align} \)
12. Giải bài 1.67 trang 38 SBT Giải tích 12
Cho hàm số
\(y=\dfrac{4-x}{2x+3m}\)
a) Xét tính đơn điệu của hàm số
b) Chứng minh rằng với mọi m, tiệm cận ngang của đồ thị \(\left( {{C}_{m}} \right)\) của hàm số đã cho luôn đi qua điểm \(B\left(-\dfrac 7 4;-\dfrac 1 2 \right)\)
c) Biện luận theo m số giao điểm của \(\left( {{C}_{m}} \right)\) và đường phân giác của góc phần tư thứ nhất
Phương pháp giải
a)
- Tính y'.
- Biện luận theo m dấu của y', từ đó suy ra tính đơn điệu của hàm số.
b)
- Tìm phương trình đường tiệm cận ngang của đồ thị hàm số.
Sử dụng định nghĩa: \(\mathop {\lim }\limits_{x \to + \infty } y = {y_0}\,\,hoặc\,\,\mathop {\lim }\limits_{x \to - \infty } y = {y_0} \,\, thì \,\,y = {y_0}\) là TCN của đồ thị hàm số.
c)
- Xét phương trình hoành độ giao điểm.
- Biện luận số giao điểm dựa vào số nghiệm của phương trình vừa xét.
Hướng dẫn giải
a)
TXĐ: \(\mathbb{R}\backslash \left\{ -\dfrac{3m}{2} \right\} \)
\(y'=\dfrac{-2x-3m-2\left( 4-x \right)}{{{\left( 2x+3m \right)}^{2}}}=\dfrac{-3m-8}{{{\left( 2x+3m \right)}^{2}}} \)
+) Nếu \(m<-\dfrac{8}{3}\) thì \(y'>0\), hàm số đồng biến trên các khoảng \(\left( -\infty ;-\dfrac{3m}{2} \right);\,\left( -\dfrac{3m}{2};+\infty \right) \)
+) Nếu \(m>-\dfrac{8}{3}\) thì \(y'<0\), hàm số nghịch biến trên các khoảng \(\left( -\infty ;-\dfrac{3m}{2} \right);\,\left( -\dfrac{3m}{2};+\infty \right) \)
+) Nếu \(m=-\dfrac{8}{3} \) thì \(y=-\dfrac{1}{2}\) khi \(x\ne 4 \)
b)
Ta có:
\(\lim\limits_{x\to\pm \infty}\,\dfrac{4-x}{2x+3m}=-\dfrac{1}{2} \)
Nên với mọi , đường thẳng \(y =-\dfrac 1 2\) luôn là tiệm cận ngang và đi qua điểm \(B\left( -\dfrac{7}{4};-\dfrac{1}{2} \right) \)
c)
Số giao điểm của \((C_m)\) và đường phân giác của góc phần tư thứ nhất là số nghiệm của phương trình
\(\begin{aligned} & \dfrac{4-x}{2x+3m}=x \\ & \Leftrightarrow 4-x=2{{x}^{2}}+3mx \\ & \Leftrightarrow 2{{x}^{2}}+\left( 3m+1 \right)x-4=0\,\,\,\,\,\,\,\,\,\,\,\,\,(*) \\ \end{aligned} \)
Thay \(x=-\dfrac{3m}{2}\) vào (*), ta có:
\(\begin{aligned} & 2{{\left( -\dfrac{3m}{2} \right)}^{2}}-\dfrac{9{{m}^{2}}}{2}-\dfrac{3m}{2}-4=\dfrac{9{{m}^{2}}}{2}-\dfrac{9{{m}^{2}}}{2}-\dfrac{3m}{2}-4\ne 0 \\ & \Rightarrow m\ne -\dfrac{8}{3} \\ \end{aligned} \)
Như vậy để \(x\ne -\dfrac{3m}{2}\Rightarrow m\ne -\dfrac{8}{3} \)
Ta có: \( \Delta ={{\left( 3m+1 \right)}^{2}}+32>0,\,\,\forall m\). Từ đó suy ra với \( m\ne -\dfrac{8}{3}\) đường thẳng \(y=x\) luôn cắt tại hai điểm phân biệt
13. Giải bài 1.68 trang 38 SBT Giải tích 12
Hàm số \(y=x^3+(m+3)x^2+mx-2\) đạt cực tiểu tại \(x=1\). Khi :
A. \(m=1\)
B. \(m=2\)
C. \(m=-3\)
D. \(m=4\)
Phương pháp giải
Hàm đa thức bậc ba \(y = f\left( x \right)\,\, đạt\, cực\, tiểu\, tại \,\,x = {x_0} \Leftrightarrow \left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) > 0\end{array} \right.\)
Hướng dẫn giải
Ta có:
\(y'=3x^2+2(m+3)x+m\)
\(y''=6x+2(m+3)\)
Vì hàm số đạt cực tiểu tại \(x=1\) nên ta có:
\(y'(1)=3+2(m+3)+m=0\Leftrightarrow 3m+9=0\Leftrightarrow m=-3\)
Với \(m =-3\) ta có:
\(y''=6x\\ \Rightarrow y''(1)=6>0\)
Thỏa mãn, vậy với \(m =-3\) hàm số đạt cực tiểu tại \(x=1\)
Chọn C.
14. Giải bài 1.69 trang 38 SBT Giải tích 12
Hàm số \(y=x^4+(m^2-4)x^2+5\) có ba cực trị khi :
A. \(-2 < m < 2\)
B. \(m=2\)
C. \(m < -2\)
D. \(m > 2\)
Phương pháp giải
Hàm đa thức bậc bốn có ba điểm cực trị \(\Leftrightarrow \) phương trình y' = 0 có ba nghiệm phân biệt.
Hướng dẫn giải
\(y'=4x^3+2(m^2-4)x\\ \Rightarrow y'=0\Leftrightarrow \left[\begin{align}&x=0\\&x^2=-\dfrac{m^2-4}{2}\\ \end{align}\right.\)
Để đồ thị hàm số có ba cực trị thì phương trình \(y'=0\) có ba nghiệm phân biệt, hay:
\(-\dfrac{m^2-4}{2}>0\Leftrightarrow -2< m<2\)
Chọn A
15. Giải bài 1.70 trang 38 SBT Giải tích 12
Biểu thức tổng quát của hàm số có đồ thị như hình 1.6 là :
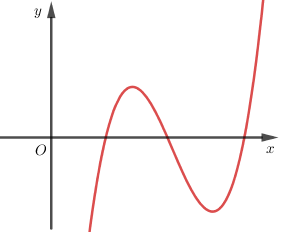
A. \(y=ax^2+bx+c\) với \(a\ne 0\)
B. \(y=ax^3+cx+d\) với \(a<0\)
C. \(y=ax^3+bx^2+cx+d\) với \(a> 0\) và \(b^2-3ac>0\)
D. \(y=x^3\)
Phương pháp giải
- Nhận xét dáng đồ thị, số điểm cực trị và loại đáp án.
Hướng dẫn giải
Quan sát dáng đồ thị ta thấy:
+ Đây là đồ thị hàm đa thức bậc ba. Loại A.
+ Có \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty ,\mathop {\lim }\limits_{x \to - \infty } y = - \infty\) nên hệ số \(a > 0\). Loại B.
+ Đáp án D có \(y' = 3{x^2} \ge 0,\forall x\) nên hàm số đồng biến trên R và không có cực trị nên loại D.
Chọn C.
16. Giải bài 1.71 trang 39 SBT Giải tích 12
Xác định giá trị của tham số m để hàm số
\(y=x^3-3(m-1)x^2-3(m+1)x-5\) có cực trị.
A. \( m > 0\)
B. \(-1 < m< 1\)
C. \(m\le 0\)
D. \(\forall m \in \mathbb R\)
Phương pháp giải
Hàm số bậc ba có cực trị nếu và chỉ nếu phương trình y' = 0 có hai nghiệm phân biệt.
Hướng dẫn giải
\(y'=3x^2-6(m-1)x-3(m+1)\,\,(*)\)
Để hàm số có cực trị phương trình (*) có hai nghiệm phân biệt, hay:
\(\Delta'=9(m-1)^2+9(m+1)>0\\ \Leftrightarrow 9m^2-9m+18>0\,\,\forall m\in \mathbb R\)
Chọn D.
17. Giải bài 1.72 trang 39 SBT Giải tích 12
Phương trình tiếp tuyến của đồ thị hàm số \(y=x^4-2x^2\) tại điểm có hoành độ \(x=-2\) là :
A. \(y=-24x+40\)
B. \( y=24 x-40\)
C. \(y=-24x-40\)
D. \(y=-24 x\)
Phương pháp giải
- Tính y'.
- Phương trình tiếp tuyến tại điểm \(\left( {{x_0};f\left( {{x_0}} \right)} \right)\) được viết theo công thức \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right.\)
Hướng dẫn giải
Điểm có hoành độ là \(-2\) thì có tung độ là \(8\)
\(y'=4x^3-4x\\ y'(-2)=-24\)
Vậy phương trình tiếp tuyến của đồ thị hàm số tại điểm \(x=-2\) là:
\(y=-24(x+2)+8=-24x-40\)
Chọn C
18. Giải bài 1.73 trang 39 SBT Giải tích 12
Phương trình tiếp tuyến của đồ thị hàm số \(y=x^4-2x^2-3\) song song với đường thẳng \(y=24x-1\) là :
A. \(y=24x-43\)
B. \(y=-24x-43\)
C. \(y=24x+43\)
D. \(y=24x+1\)
Phương pháp giải
- Giải phương trình y' = k tìm hoành độ tiếp điểm.
- Từ đó suy ra tiếp điểm và viết phương trình tiếp tuyến theo công thức \(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + f\left( {{x_0}} \right)\)
Hướng dẫn giải
\(y'=4x^3-4x\)
Vì tiếp tuyến song song với đường thẳng \(y=24x-1\) nên hệ số góc của tiếp tuyến là 24.
Gọi \((x_0;y_0)\) là tiếp điểm, ta có:
\(y'(x_0)=4x_0^3-4x_0=24\\ \Rightarrow y'(x_0)=0\Leftrightarrow x_0=2\Rightarrow y_0=5\)
Phương trình tiếp tuyến
\(y=24(x-2)+5=24x-43\)
Chọn A
19. Giải bài 1.74 trang 39 SBT Giải tích 12
Giao điểm của đồ thị hàm số \(y=\dfrac{2x+1}{2x-1}\) và đường thẳng \(y=x+2\) là:
A. \( (1;3)\) và \(\left(-\dfrac 3 2 ;\dfrac 1 2\right)\)
B. \( (1;3)\) và \(\left(0;2\right)\)
C. \( (0;-1)\) và \(\left(-\dfrac 3 2 ;\dfrac 1 2\right)\)
D. \( (0;-1)\) và \(\left(0;2\right)\)
Phương pháp giải
- Xét phương trình hoành độ giao điểm.
- Giải phương trình và kết luận.
Hướng dẫn giải
Xét phương trình hoành độ giao điểm
\(\begin{aligned} & \dfrac{2x+1}{2x-1}=x+2 \\ & \Rightarrow 2x+1=\left( x+2 \right)\left( 2x-1 \right) \\ & \Leftrightarrow \left[ \begin{aligned} & x=1 \\ & x=\dfrac{-3}{2} \\ \end{aligned} \right. \\ \end{aligned} \)
Vậy có hai giao điểm là \( \left( 1;3 \right);\,\,\left( -\dfrac{3}{2};\dfrac{1}{2} \right) \)
Chọn A.
Các em hãy luyện tập bài trắc nghiệm Khảo sát sự biến thiên và vẽ đồ thị của hàm số Toán 12 sau để nắm rõ thêm kiến thức bài học.
Tham khảo thêm
- doc Giải bài tập SBT Toán 12 Bài 1: Sự đồng biến, nghịch biến của hàm số
- doc Giải bài tập SBT Toán 12 Bài 2: Cực trị của hàm số
- doc Giải bài tập SBT Toán 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- doc Giải bài tập SBT Toán 12 Bài 4: Đường tiệm cận



