Toán 9 Ôn tập chương 2: Đường tròn
Sau đây chúng ta cùng ôn tập lại chương Đường tròn gồm các kiến thức về tính đối xứng của đường tròn, liên hệ giữa dây và khoảng cách từ tâm đến dây, vị trí tương đối của 2 đường tròn, dấu hiệu nhận biết tiếp tuyến của đường tròn,.....
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Khái niệm về đường kính
Trong các dây của một đường tròn, dây lớn nhất là đường kính
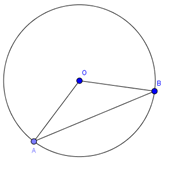
Trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây đó
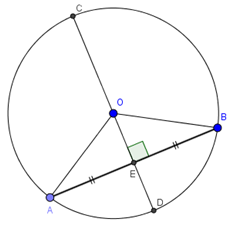
Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
1.2. Liên hệ giữa dây và khoảng cách từ tâm đến dây
Định lý 1:
Trong một đường tròn
a) Hai dây bằng nhau thì cách đều tâm
b) Hai dây cách đều tâm thì bằng nhau
Định lý 2:
Trong một đường tròn
a) Dây nào lớn hơn thì dây đó gần tâm hơn
b) Dây nào gần tâm hơn thì dây đó lớn hơn
1.3. Ba vị trí tương đối của đường thẳng và đường tròn
a) Đường thẳng và đường tròn cắt nhau
Khi một đường thẳng a và đường tròn (O;R) có 2 điểm chung ta nói đường thẳng a và đường tròn (O; R) cắt nhau. Đường thẳng a gọi là cát tuyến của đường tròn (O; R)
Khi đó: Gọi H là hình chiếu vuông góc của O lên a thì OH là khoảng cách từ O đến a và OH
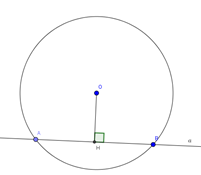
b) Đường thẳng và đường tròn tiếp xúc nhau
Khi đường thẳng a và đường tròn (O; R) có 1 điểm chung tại C ta nói đường thẳng a và đường tròn (O; R) tiếp xúc nhau
Ta còn nói đường thẳng a là tiếp tuyến của đường tròn. Điểm C gọi là tiếp điểm và OC chính là khoảng cách từ O đến a. Khi đó OH = R
Định lý:
Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm
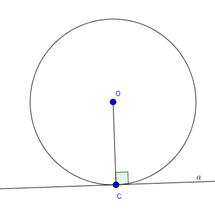
c) Đường thẳng và đường tròn không giao nhau
Khi đường thẳng a và đường tròn (O) không có điểm chung nào thì ta nói đường thẳng a và đường tròn (O) không giao nhau
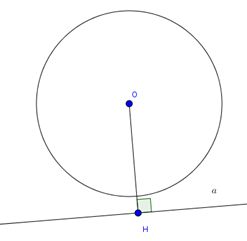
1.4. Hệ thức giữa khoảng cách từ tâm đường tròn tới đường thẳng và bán kính của đường tròn
Cho đường thẳng a và (O; R). Đặt OH = d là khoảng cách từ O đến đường thẳng a. Khi đó:
d < R <=> đường thẳng a cắt (O; R) tại hai điểm phân biệt
d = R <=> đường thẳng a có 1 điểm chung với (O; R) (hay đường thẳng a tiếp xúc với đường tròn (O; R))
d > R <=> đường thẳng a không có điểm chung với đường tròn (O; R)
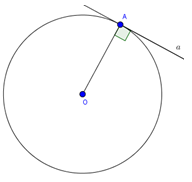
1.5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
Định lý:
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn
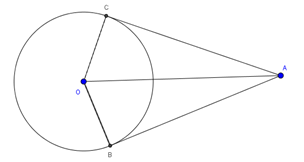
1.6. Định lý về hai tiếp tuyến cắt nhau
Định lý:
Nếu hai tiếp tuyến của đường tròn cắt nhau tại 1 điểm thì:
- Điểm đó cách đều hai tiếp điểm
- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến
- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm
- Góc tạo bởi hai tiếp tuyến AB và AC là góc BAC
- Góc tạo bởi hai bán kính đi qua các tiếp điểm là BOC
1.7. Đường tròn nội tiếp tam giác
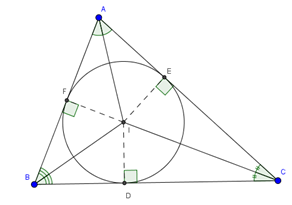
- Đường tròn tiếp xúc với 3 cạnh một tam giác gọi là đường nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn
- Tâm của đường tròn nội tiếp tam giác là giao của các đường phân giác trong của tam giác đó.
1.8. Tính chất đường nội tâm
Định lý:
- Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng với nhau qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây chung
- Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm
1.9. Hệ thức giữa đoạn nối tâm và các bán kính
Xét hai đường tròn (O; R) và (O'; r) trong đó \(R \ge r\)
a) Hai đường tròn cắt nhau
Nếu hai đường tròn (O; R) và (O'; r) cắt nhau thì R - r < OO' < R + r
b) Hai đường tròn tiếp xúc nhau
- Nếu (O) và (O') tiếp xúc ngoài thì: OO' = R + r
- Nếu (O) và (O') tiếp xúc trong thì: OO' = R - r
c) Hai đường tròn không giao nhau
- Nếu hai đường tròn (O) và (O') ở ngoài thì OO' > R -r
1.10. Tiếp tuyến chung của hai đường tròn
Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với cả hai đường tròn đó
- Tiếp tuyến chung ngoài không cắt đoạn nội tâm
- Tiếp tuyến chung trong cắt đoạn nối tâm
- Nếu đường tròn (O) đựng đường tròn (O') thì OO' < R - r
- Nếu hai đường tròn (O) và (O') đồng tâm thì OO' = 0
2. Bài tập minh họa
2.1. Bài tập 1
Cho đường tròn (O;R) và 2 dây AB và CD bằng nhau và vuông góc với nhau tại I. Giả sử IA=4, IB=8. Khoảng cách từ tâm O tới AB là d và tới CD là d'
Giá trị của d và d'
Hướng dẫn giải
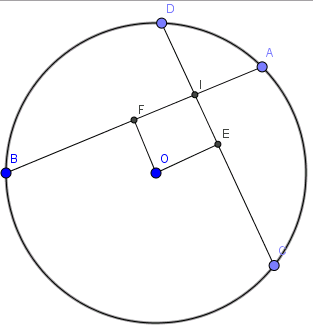
Gọi E, F lần lượt là hình chiếu vuông góc của O lên CD, AB. Vì tứ giác OFIE có 3 góc vuông nên OFIE là hình chữ nhật
ta lại có OE=OF do AB=CD nên OFIE là hình vuông khi đó:
\(OE=OF=EI=FI=FA-IA=\frac{AB}{2}-IA=\frac{IA+IB}{2}-IA=2\)
2.2. Bài tập 2
Cho (O;10), dây AB=20. Vẽ dây CD song song với AB và có khoảng cách tới AB là 8. Độ dài dây CD là?
Hướng dẫn giải
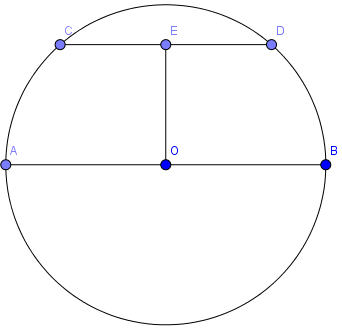
Vì đường kính của đường tròn là 20 nên AB đi qua tâm đường tròn.
Gọi E là trung điểm của CD \(\Rightarrow OE\perp AB\)
Trong tam giác OEC vuông tại E, ta có: \(CE=\sqrt{CO^2-OE^2}=6\)
\(CD=2CE=12\)
2.3. Bài tập 3
Cho đường tròn (O;3). Một điểm A cách O một khoảng là 8. Kẻ tiếp tuyến AB với (O) (B là tiếp điểm). Độ dài AB là:
Hướng dẫn giải
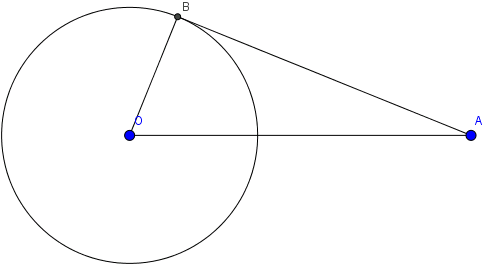
Dựa vào hình trên, ta thấy rằng:
Tam giác AOB vuông tại B
\(\Rightarrow AB=\sqrt{AO^2-OB^2}=\sqrt{55}\)
2.4. Bài tập 4
Cho đường tròn (O;4). Một điểm A cách O một khoảng là 12. Kẻ tiếp tuyến AB với (O) (B là tiếp điểm). OA cắt đường tròn tại C. Qua C dựng đường thẳng song song với OB, cắt AB tại D. Độ lớn của CD là?
Hướng dẫn giải
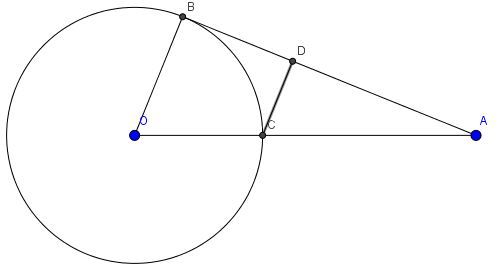
Ta có: \(CD//OB\Rightarrow \frac{CD}{OB}=\frac{AC}{AO}\)\(\Rightarrow CD=\frac{AC.OB}{AO}=\frac{8.4}{12}=\frac{8}{3}\)
2.5. Bài tập 5
Cho tam giác ABC vuông tại A có AB=6, AC=8. Đường tròn (I;r) nội tiếp tam giác ABC. Giá trị của r là:
Hướng dẫn giải
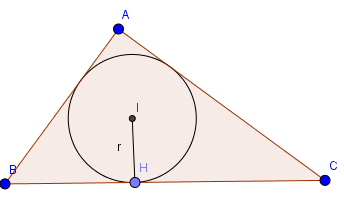
\(S_{ABC}=\frac{1}{2}.AB.AC=24=p.r\Rightarrow r=\frac{24}{\frac{1}{2}.(AB+AC+\sqrt{AB^2+AC^2})}=2\)
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ các đường kính AOB, AO’C. Gọi DE là tiếp tuyến chung của hai đường tròn (D ∈ (O), E ∈ (O’)). Gọi M là giao điểm của BD và CE.
a. Tính số đo góc DAE.
b. Tứ giác ADME là hình gì? Vì sao ?
c. Chứng minh rằng MA là tiếp tuyến chung của hai đường tròn.
Câu 2: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài MN của hai đường tròn (M ∈ (O), N ∈ (O’)). Gọi P là điểm đối xứng với M qua OO’, Q là điểm đối xứng với N qua OO’. Chứng minh rằng:
a. MNQP là hình thang cân.
b. PQ là tiếp tuyến chung của hai đường tròn (O) và (O’).
c. MN + PQ = MP + NQ.
Câu 3: Cho hai đường tròn (O; 2cm), (O’; 3cm), OO’ = 6cm
a. Hai đường tròn (O) và (O’) có vị trí tương đối như thế nào với nhau?
b. Vẽ đường tròn (O’; 1cm) rồi kẻ tiếp tuyến OA với đường tròn đó (A là tiếp điểm). Tia O’A cắt đường tròn (O’; 3cm) ở B. Kẻ bán kính OC của đường tròn (O) song song với O’B, B và C thuộc cùng một nửa mặt phẳng có bờ OO’. Chứng minh rằng BC là tiếp tuyến chung của hai đường tròn (O; 2cm), (O’; 3cm).
c. Tính độ dài BC
d. Gọi I là giao điểm của BC và OO’/ Tính độ dài IO
Câu 4: Cho đường tròn (O; R), điểm A nằm bên ngoài đường tròn (R < OA < 3R). Vẽ đường tròn (A; 2R)
a. Hai đường tròn (O) và (A) có vị trí tương đối như thế nào với nhau?
b. Gọi B là một giao điểm của hai đường tròn trên. Vẽ đường kính BOC của đường tròn (O). Gọi D là giao điểm (khác C) của AC và đường tròn (O). Chứng minh rằng AD = DC
3.2. Bài tập trắc nghiệm
Câu 1: Cho hai đường tròn (O;4) và (O';4) cắt nhau tại A và B. Biết OO'=6. Độ dài dây cung chung AB là:
A. \(AB=\sqrt{7}\)
B. \(AB=2\sqrt{7}\)
C. \(AB=7\)
D. \(AB=14\)
Câu 2: Cho (O). Từ một điểm M ngoài (O) vé hai tiếp tuyến MA, MB sao cho \(\widehat{AMB}=60^{\circ}\). Biết chu vi của tam giác MAB là 30. Tính độ dài dây AB
A. \(5\)
B. \(5\sqrt{2}\)
C. \(5\sqrt{3}\)
D. \(10\)
Câu 3: Cho đường tròn (O;5) và (O';4). Biết OO'=10. Vị trí tương đối của hai đường tròn là
A. Không cắt nhau
B. Cắt nhau
C. Tiếp xúc trong
D. Tiếp xúc ngoài
Câu 4: Cho tam giác ABC có AB=5, AC=12, BC=13. Khi đó:
A. AB là tiếp tuyến của (C;5)
B. AC là tiếp tuyến của (B;5)
C. AB là tiếp tuyến của (B;12)
D. AC là tiếp tuyến của (C;13)
Câu 5: Cho đường tròn (O;R) và một dây CD. Từ O kẻ tia vuông góc với CD tại M, cắt (O) tại H (M nằm giữa O và H). Biết CD=16, MH=4. R=?
A. 10
B. 12
C. 14
D. 16
4. Kết luận
Qua bài học này, các em nắm được một số nội dung chính như sau:
- Hệ thống hóa được các kiến thức về tính đối xứng của đường tròn, liên hệ giữa dây và khoảng cách từ tâm đến dây, vị trí tương đối của 2 đường tròn, của đường thẳng và đường tròn.
- Thành thạo kĩ năng vẽ hình, vận dụng các kiến thức đã học vào giải các bài tập về tính toán, chứng minh.
Tham khảo thêm
- doc Toán 9 Chương 2 Bài 1: Sự xác định của đường tròn và tính chất đối xứng của đường tròn
- doc Toán 9 Chương 2 Bài 2: Đường kính và dây của đường tròn
- doc Toán 9 Chương 2 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây
- doc Toán 9 Chương 2 Bài 4: Vị trí tương đối của đường thẳng và đường tròn
- doc Toán 9 Chương 2 Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn
- doc Toán 9 Chương 2 Bài 6: Tính chất của hai tiếp tuyến cắt nhau
- doc Toán 9 Chương 2 Bài 7: Vị trí tương đối của hai đường tròn
- doc Toán 9 Chương 2 Bài 8: Vị trí tương đối của hai đường tròn (tiếp theo)



