Toán 9 Chương 2 Bài 6: Tính chất của hai tiếp tuyến cắt nhau

Định lý

Nếu hai tiếp tuyến của đường tròn cắt nhau tại 1 điểm thì

• Điểm đó cách đều hai tiếp điểm
• Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến
• Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm

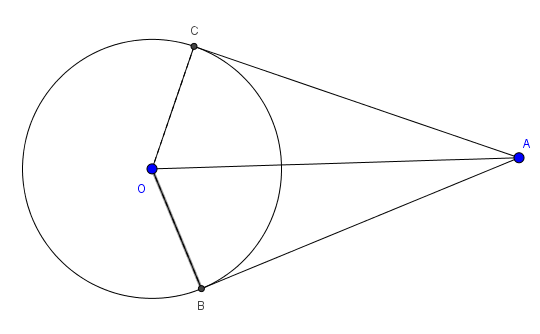
- Góc tạo bởi hai tiếp tuyến AB và AC là góc BAC

- Góc tạo bởi hai bán kính đi qua các tiếp điểm là BOC

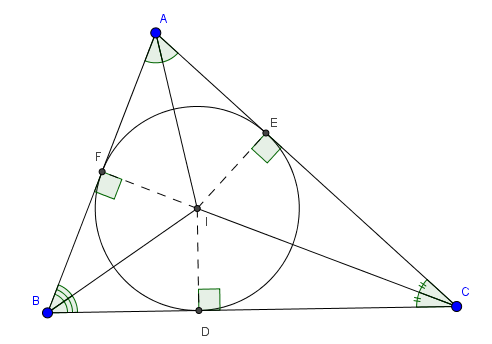
• Đường tròn tiếp xúc với 3 cạnh một tam giác gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn.
• Tâm của đường tròn nội tiếp tam giác là giao của các đường phân giác trong của tam giác đó

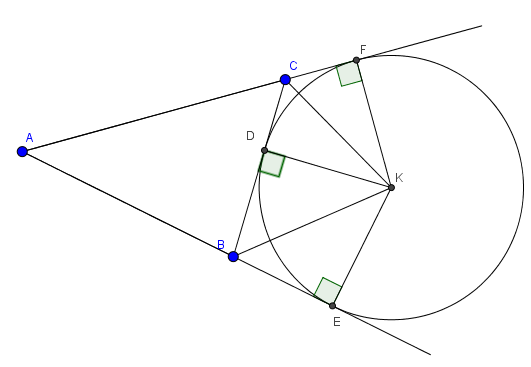
• Đường tròn tiếp xúc với một cạnh của một tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia gọi là đường tròn bàng tiếp tam giác. ( Hình trên gọi là Đường tròn bàng tiếp trong góc A của tam giác ABC)
• Tâm của đường tròn bàng tiếp trong góc A là giao điểm của hai đường phân giác ngoài các góc B và C hoặc là giao điểm của đường phân giác trong góc A với phân giác ngoài góc B (hoặc C).
• Với một tam giác có 3 đường tròn bàng tiếp tam giác

Câu 1: Cho (O) từ M ngoài đường tròn kẻ hai tiếp tuyến MA, MB của (O). Trên tia OB lấy C sao cho OB=BC. CMR: \(\widehat{BMC}=\frac{1}{2}.\widehat{BMA}\)

Hướng dẫn giải

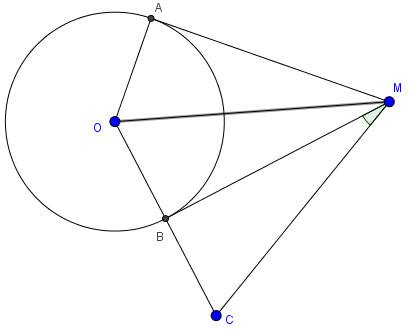
Ta có: MO là tia phân giác góc AMB nên \(\widehat{OMB}=\frac{1}{2}.\widehat{BMA}\)

Xét tam giác OMC có OB vừa là đường cao vừa là trung tuyến nên tam giác MOC cân tại M suy ra MB là phân giác góc OMC

\(\Rightarrow \widehat{BMC}=\widehat{OMB}=\frac{1}{2}.\widehat{BMA}\)

Câu 2: Cho đường tròn (O;R) và một điểm A ở ngoài đường tròn. Vẽ các tiếp tuyến AB, AC. CMR: \(\widehat{BAC}=60^{\circ}\Leftrightarrow OA=2R\)

Hướng dẫn giải

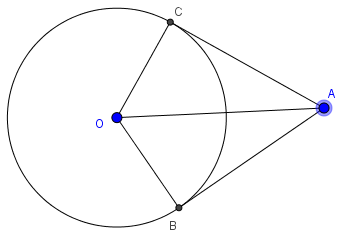
 \(\widehat{BAC}=60^o\Leftrightarrow \widehat{OAB}=30^o\Leftrightarrow sin \widehat{OAB}=\frac{1}{2}=\frac{OB}{OA}=\frac{R}{OA}\Leftrightarrow OA=2R\)

Câu 3: Chứng minh rằng diện tích tam giác ngoại tiếp một đường tròn được tính theo công thức: S=pr, Trong đó p là nửa chu vi tam giác, r là bán kính đường tròn nội tiếp

Hướng dẫn giải

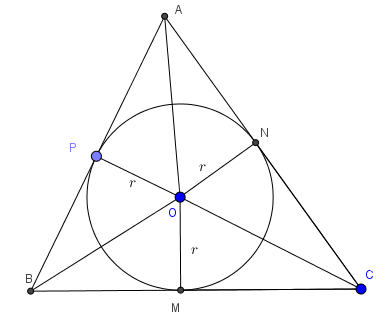
\(S_{ABC}=S_{AOB}+S_{BOC}+S_{AOC}=\frac{1}{2}.(AB+BC+AC).r=p.r\)

Câu 1: Cho nửa đường tròn tâm O đường kính AB. Vẽ các tia Ax vuông góc AB, By vuông góc với AB ở cùng phía với nửa đường tròn. I là một điểm trên nửa đường tròn đó. Tiếp tuyến tại I cắt Ax, By lần lượt tại C, D.

a) CMR: Tam giác COD là tam giác vuông 

b) Tim vị trí điểm I để chu vi tứ giác ACDB là nhỏ nhất. Tính chu vi đó theo R

Hướng dẫn giải

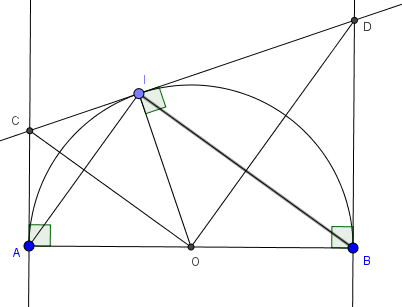
a) Ta có tam giác IAB vuông tại I 

Gọi E là giao điểm của AI và CO, F là giao điểm của IB và OD. Xét tứ giác IEOF có 3 góc vuông nên IEOF là hình chữ nhật suy ra \(\widehat{EOF}=90^{\circ}\Rightarrow \Delta COD\) vuông tại O

b) Vì tiếp tuyến tại A và I cắt nhau tại C nên CA=CI, tương tự DI=DB \(\Rightarrow AC+BD=CD\). Ta lại có \(CD\geq AB\) vì AB là đoạn vuông góc của 2 đường song song là AC và BD 

Khi đó: \(2P_{ACDB}=AC+BD+CD+AB=2CD+AB\geq 3.AB=3R\)

Câu 2: Cho tam giác ABC cân tại A nội tiếp đường tròn (O) . Các tiếp tuyến của (O) vẽ từ A và C cắt nhau tại M. Trên tia AM lấy D sao cho AD=BC. CMR: AC, BD, OM đồng quy

Hướng dẫn giải

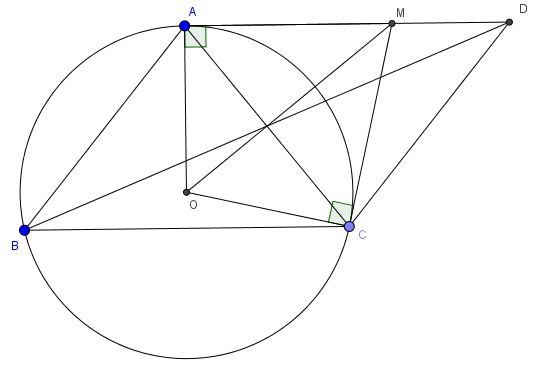
Trước tiên ta sẽ chứng minh ABCD là hình bình hành

Ta có AO vuông góc BC, AO vuông góc AD nên \(AD\parallel BC\), mà AD=BC nên ABCD là hình bình hành

Gọi E là giao điểm của AC và OM. theo tính chất hai tiếp tuyến cắt nhau thì E là trung điểm AC (do tam giác MAC cân tại M, có ME đường cao)

Do ABCD là hình bình hành nên đường chéo sẽ qua trong điểm mỗi đường. Vậy BD đi qua E

Câu 1: Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AM, AN với đường tròn (M, N là các tiếp điểm)

a. Chứng minh rằng OA ⊥ MN

b. Vẽ đường kính NOC. Chứng minh rằng MC // AO

c. Tính độ dài các cạnh của tam giác AMN biết OM = 3cm, OA = 5cm

Câu 2: Cho đường tròn (O), điểm M nằm bên ngoài đường tròn. Kẻ tiếp tuyến MD, ME với đường tròn (D, E là các tiếp điểm). Qua I thuộc cung nhỏ DE, kẻ tiếp tuyến với đường tròn, cắt MD và ME theo thứ tự ở P và Q. Biết MD = 4cm, tính chu vi tam giác MPQ

Câu 3: Cho góc xOy khác góc bẹt, điểm A nằm trên tia Ox. Dựng đường tròn (I) đi qua A và tiếp xúc với hai cạnh của góc xOy

Câu 4: Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc tia Ax. Qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N.

a. Tính số đo góc MON

b. Chứng minh rằng MN = AM + BN

c. Chứng minh rằng AM.BN = R2 (R là bán kính của nửa đường tròn)

Câu 1: Phát biểu nào sau đây là đúng

A. Có 3 đường tròn nội tiếp một tam giác

B. Có chỉ một đường tròn bàng tiếp một tam giác

C. Giao điểm của các đường phân giác trong chính là tâm đường tròn bàng tiếp tam giác đó

D. giao điểm của phân giác trong góc A và phân giác ngoài tại B là tâm đường tròn bầng tiếp trong góc A

Câu 2: Cho tam giác ACB vuông tại A. O là tâm đường tròn nội tiếp tam giác ABC. D, E, F lần lượt là các tiếp điểm trên AB, AC, BC. Hệ thức nào đúng

A. AD=AC+AB-BC

B. 2AD=AB+AC-BC

C. 2EC=AB+AC-BC

D. 2BD=AC+BC-AB

Câu 3: Cho đường tròn (O). M là điểm ngoài đường tròn, vẽ hai tiếp tuyến MA, MB của (O). Khẳng định nào sau đây là sai

A. \(MA=MB\)

B. \(OM\perp AB\)

C. \(\widehat{OMA}=\widehat{OMB}\)

D. \(OM=2.AB\)

Câu 4: Cho tam giác ABC vuông tại A có AB=3, AC=4. Đường tròn (I;r) nội tiếp tam giác ABC. Giá trị của r là:

A. 1

B. 2

C. 3

D. 4

Câu 5: Cho tam giác ABC ngoại tiếp đường tròn (O). Biết  \(\widehat{AOC}=130^o, \widehat{OCA}=30^o\). So sánh OB và OC 

A. OB

B. OB>OC

C. OB=OC

D. Chưa đủ dữ kiện để so sánh

Qua bài học này, các em nắm được một số nọi dung chính như sau:

• Vẽ được đường tròn nội tiếp một tam giác cho trước.
• Vận dụng tính chất của hai tiếp tuyến cắt nhau vào bài tập tính toán hoặc chứng minh.
• Tìm tâm của một vật hình tròn bằng “thước phân giác”.