Toán 9 Chương 2 Bài 8: Vị trí tương đối của hai đường tròn (tiếp theo)
Mời các em học sinh tham khảo nội dung bài Vị trí tương đối của hai đường tròn gồm các kiến thức về hai đường tròn cắt nhau, hai đường tròn tiếp xúc nhau, hai đường tròn không giao nhau,...đã được eLib biên soạn đầy đủ và chi tiết.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Hệ thức giữa đoạn nối tâm và các bán kính
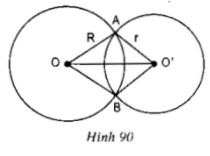
a) Hai đường tròn cắt nhau
Nếu hai đường tròn (O) và (O') cắt nhau thì R - r < OO' < R + r
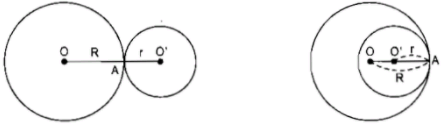
b) Hai đường tròn tiếp xúc nhau
- Nếu hai đường tròn (O) và (O') tiếp xúc ngoài thì OO' = R + r
- Nếu hai đường tròn (O) và (O') tiếp xúc trong thì OO' = R - r
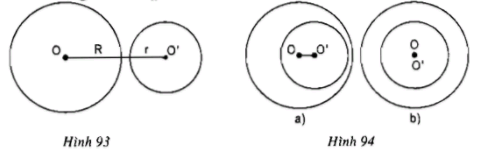
c) Hai đường tròn không giao nhau
- Nếu hai đường tròn (O) và (O') ở ngoài nhau thì OO' > R + r
- Nếu hai đường tròn (O) đựng đường tròn (O') thì OO' > R - r
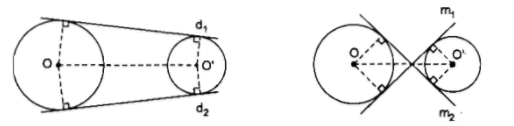
1.2. Tiếp tuyến chung của hai đường tròn
- Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với cả hai đường tròn đó
2. Bài tập minh họa
2.1. Bài tập cơ bản
Cho đường tròn tâm O bán kính OA và đường tròn đường kính OA.
a) Xác định vị trí tương đối của hai đường tròn
b) Dây AD của đường tròn lớn cắt đường tròn nhỏ ở C. CMR: AC=CD
Hướng dẫn giải
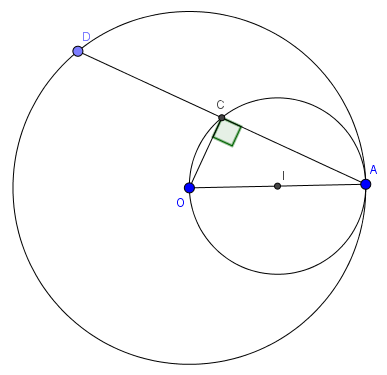
a) Hai đường tròn tâm O bán kính OA và đường tròn đường kính OA tiếp xúc trong với nhau
b) Tam giác AOC có IA=IO=IC nên tam giác đó vuông tại C hay OC vuông góc AD tại C
Vì vậy C là trung điểm của AD nên AC=CD
2.2. Bài tập nâng cao
Câu 1: Cho 2 đường tròn (O;R) và (O;r) cắt nhau tại hai điểm A và B. Vẽ đường kính AOC và AO'D
a) Chứng minh 3 điểm C, B, D thẳng hàng
b) Qua A vẽ cát tuyến cắt (O) và (O') lần lượt tại M, N. CMR: \(MN\leq CD\)
Hướng dẫn giải
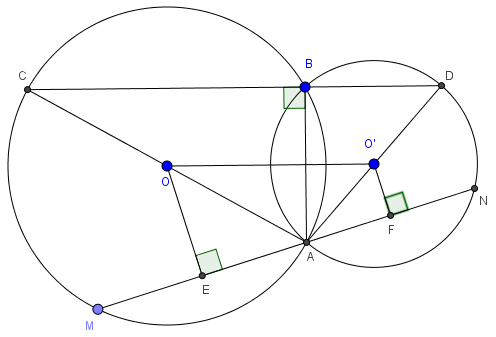
a) Tam giác ABC có AC là đường kính nên tam giác ABC vuông tại B hay \(AB\perp CB\)
Tam giác ABD có AD là đường kính nên tam giác ABD vuông tại B hay \(AB\perp BD\)
\(\Rightarrow C,B,D\) cùng thuộc đường thẳng qua B và vuông góc với AB
b) Xét tam giác ACD có OO' là đường trung bình nên: \(OO'=\frac{1}{2}.CD\)
Gọi E, F lần lượt là hình chiếu vuông góc của O và O' lên MN. Khi đó E, F lần lượt là trung điểm AM và AN
suy ra \(EF=\frac{1}{2}.MN\). Ta đưa việc so sánh CD với MN qua so sánh OO' và EF
Xét 2 đoạn thẳng OE và O'F song song với nhau. EF vuông góc với cả hai đoạn thẳng nên EF là đoạn thẳng nhỏ nhất trong các đoạn nối từ 1 điểm trên OE tới 1 điểm trên O'F
\(EF\leq OO'\Rightarrow MN\leq CD\)
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho I là trung điểm của đoạn thẳng AB. Vẽ các đường tròn (I; IA) và (B; BA).
a. Hai đường tròn (I) và (B) nói trên có vị trí tương đối như thế nào với nhau? Vì sao?
b. Kẻ một đường thẳng đi qua A, cắt các đường tròn (I) và (B) theo thứ tự tại M và N. So sánh các độ dài AM và MN.
Câu 2: Cho hai đường tròn đồng tâm O. Gọi AB là dây bất kì của đường tròn nhỏ. Đường thẳng AB cắt đường tròn lớn ở C và D (A nằm giữa B và C). So sánh các độ dài AC và BD.
Câu 3: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Gọi CD là tiếp tuyến chung ngoài của hai đường tròn (C ∈ (O), D ∈ (O’))
a. Tính số đo góc CAD
b. Tính độ dài CD biết OA = 4,5cm, O’A = 2cm
Câu 4: Cho hai đường tròn đồng tâm O. Một đường tròn (O’) cắt một đường tròn tâm O tại A, B và cắt đường tròn tâm O còn lại tại C, D. Chứng minh rằng AB // CD.
3.2. Bài tập trắc nghiệm
Câu 1: Cho 2 đường tròn (O;R) và (O';r), R>r
Trong các phát biểu sau phát biểu nào là phát biểu sai
A. Hai đường tròn (O) và (O') cắt nhau khi và chỉ khi R-r
B. Hai đường tròn (O) và (O') tiếp xúc ngoài khi và chỉ khi OO'=R-r
C. Hai đường tròn (O) và (O') tiếp xúc trong khi và chỉ khi OO'=R-r
D. Hai đường tròn (O) và (O') gọi là ngoài nhau khi và chỉ khi OO'>R+r
Câu 2: Cho 3 đường tròn (A), (B), (C) có cùng bán kính R đôi một tiếp xúc nhau. Gọi D, E, F là các tiếp điểm. Diện tích tam giác DEF là:
A. \(\frac{R^2\sqrt{3}}{2}\)
B. \(\frac{R^2\sqrt{3}}{3}\)
C. \(\frac{R^2\sqrt{3}}{6}\)
D. \(\frac{R^2\sqrt{3}}{4}\)
Câu 3: Cho đường tròn (O;10) và (O';3). Biết OO'=8. Vị trí tương đối của hai đường tròn là
A. (O) chứa (O')
B. Cắt nhau
C. Tiếp xúc trong
D. Tiếp xúc ngoài
Câu 4: Cho hai đường tròn (O;5) và (O';5) cắt nhau tại A và B. Biết OO'=8. Độ dài dây cung chung AB là:
A. 4
B. 5
C. 6
D. 7
Câu 5: Cho đường tròn (O;9). Vẽ 6 đường tròn bằng nhau có bán kính R đều tiếp xúc với (O) và mỗi đường tròn đều tiếp xúc với 2 đường tròn khác bên cạnh nó. R=?
A. \(6\)
B. \(3\)
C. \(2\sqrt{3}\)
D. \(3\sqrt{3}\)
4. Kết luận
Qua bài học này, các em nắm được một số nội dung chính như sau:
- Biết được ba vị trí tương đối của hai đường tròn, tiếp tuyến chung giữa hai đường tròn.
- Vận dụng được tính chất của hai đường tròn cắt nhau, tiếp xúc nhau vào bài tập về tính toán và chứng minh.
Tham khảo thêm
- doc Toán 9 Chương 2 Bài 1: Sự xác định của đường tròn và tính chất đối xứng của đường tròn
- doc Toán 9 Chương 2 Bài 2: Đường kính và dây của đường tròn
- doc Toán 9 Chương 2 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây
- doc Toán 9 Chương 2 Bài 4: Vị trí tương đối của đường thẳng và đường tròn
- doc Toán 9 Chương 2 Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn
- doc Toán 9 Chương 2 Bài 6: Tính chất của hai tiếp tuyến cắt nhau
- doc Toán 9 Chương 2 Bài 7: Vị trí tương đối của hai đường tròn
- doc Toán 9 Ôn tập chương 2: Đường tròn