Toán 9 Chương 2 Bài 1: Sự xác định của đường tròn và tính chất đối xứng của đường tròn
Ở chương trước chúng ta đã tìm hiểu nhiều về tam giác đặc biệt là tam giác vuông. Chương tiếp theo chúng ta sẽ tìm hiểu về đường tròn và những tính chất của nó. Bài đầu tiên ta sẽ tìm hiểu Sự xác định đường tròn và tính chất đối xứng của đường tròn
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Nhắc lại về đường tròn
Đường tròn tâm O bán kính R (R>0) là hình gồm các điểm cách điểm O một khoảng bằng R kí hiệu là (O;R).
- M nằm trên đường tròn (0;R) Khi và chỉ khi OM=R
- M nằm bên ngoài đường tròn khi và chỉ khi OM>R
- M nằm bên trong đường tròn khi và chỉ khi OM
1.2. Cách xác định đường tròn
Ta đã biết: Một đường tròn được xác định khi biết tâm và bán kính của đường tròn đó, hoặc khi biết 1 đoạn thẳng là đường kính của đường tròn đó
Qua 3 điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn.
Chú ý:
Không vẽ được đường tròn nào đi qua ba điểm thẳng hàng
Đường tròn đi qua 3 đỉnh của một tâm giác được gọi là đường tròn ngoại tiếp tam giác
1.3. Tâm đối xứng
Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xưng của đường tròn đó
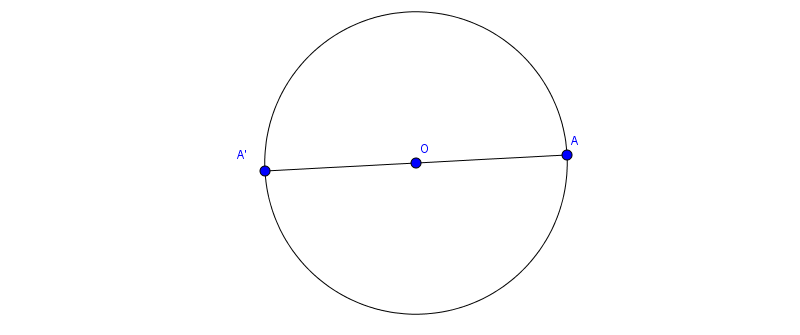
1.4. Trục đối xứng
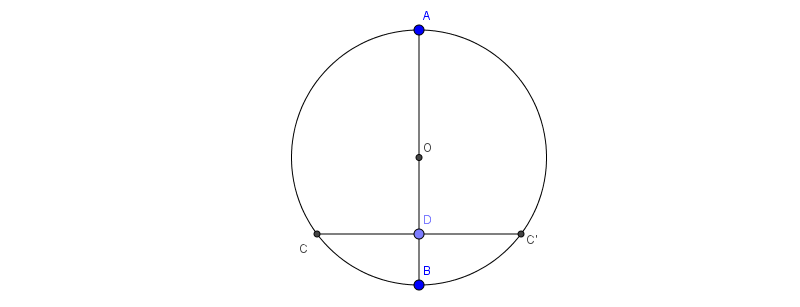
Đường tròn là hình có trục đối xứng, Bất kì đường kính nào cũng là trục đối xứng của đường tròn
2. Bài tập minh họa
2.1. Bài tập cơ bản
Câu 1: Chứng minh rằng đường tròn ngoại tiếp tam giác vuông có tâm chính là trung điểm cạnh huyền.
Hướng dẫn giải
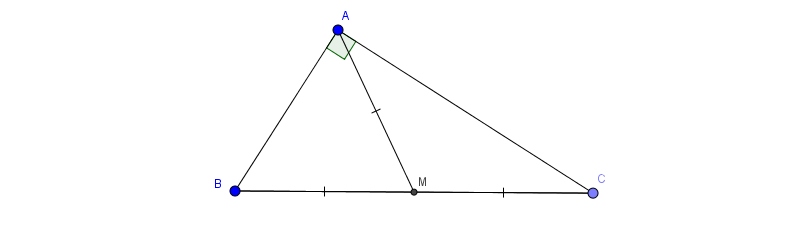
Xét tam giác ABC vuông tại A
Gọi M là trung điểm BC nên MB=MC. Dễ dàng chứng minh được MA=MB=MC từ đó suy ra đường tròn ngoại tiếp ABC có tâm là trung điểm cạnh huyền
( Ví dụ gọi N là trung điểm AB. theo tính chất đường trung bình thì \(MN\parallel AC\Rightarrow MN\perp AB\) MN vừa là đường cao vừa là trung tuyến của tam giác ABM nên ABM cân tại M)
Câu 2: Cho Hình chữ nhật ABCD có AB=10, BC=8. Chứng minh rằng A,B,C,D cùng thuộc một đường tròn và tính bán kính của đường tròn đó
Hướng dẫn giải
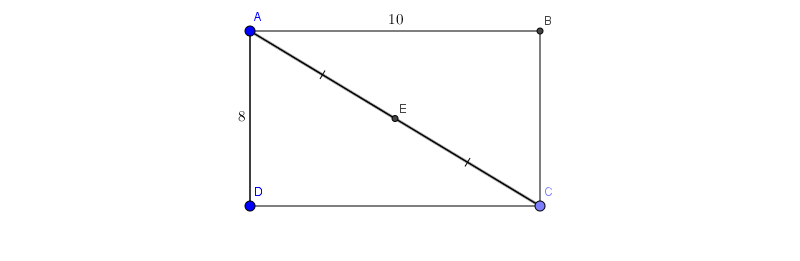
Áp dụng chứng minh như bài 1 ta có: Đường tròn ngoại tiếp Tam giác ABC có tâm là E và bán kính là EA. Tương tự cho tam giác ADC cũng có đường tròn ngoại tiếp tại E bán kính là EA
từ đó ta có A, B, C, D cùng thuộc đường tròn tâm E bán kính là AE.
\(AE=\frac{1}{2}.AC=\frac{1}{2}.\sqrt{AB^2+BC^2}=\frac{1}{2}.\sqrt{10^2+8^2}=\sqrt{41}\)
Câu 3: Cho hình thoi ABCD có góc A 60 độ, Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA. Chứng mình rằng E,F,G,H,B,D cùng thuộc 1 đường tròn
Hướng dẫn giải
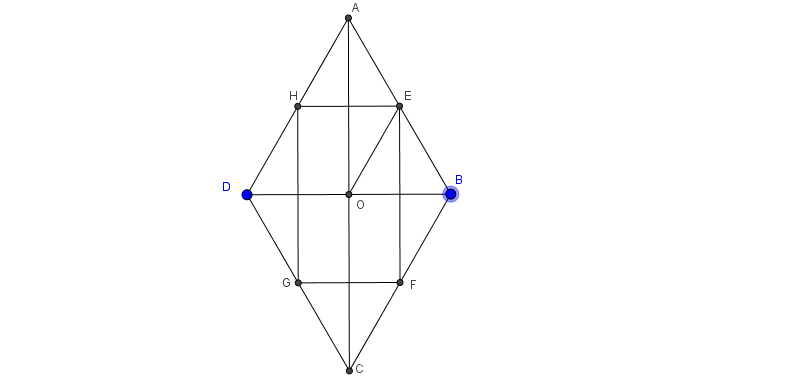
ABCD là hình thoi nên O là trung điểm AC và BD. Vì OE là đường trung bình tam giác ABD nên \(OE\parallel AD\Rightarrow \widehat{OEB}=\widehat{DAB}=60^{\circ}\)
Tam giác ABD cân có \(\widehat{A}=60^{\circ}\) nên ABD đều nên \(\widehat{ABD}=60^{\circ}\Rightarrow \Delta EOB\) đều. Tương tự cho Tam giác HOD, DOG, FOB
Kết hợp OB=OD suy ra 6 điểm trên cùng nằm trên đường tròn tâm O bán kính là OB.
2.2. Bài tập nâng cao
Câu 1: Cho đường tròn tâm (O) đường kính AB. Vẽ đường tròn tâm (I) đường kính OA. bán kính OC của (O) cắt đường tròn (I) tại D. vẽ CH vuông góc với AB.
Chứng minh tứ giác ACHD là hình thang cân
Hướng dẫn giải
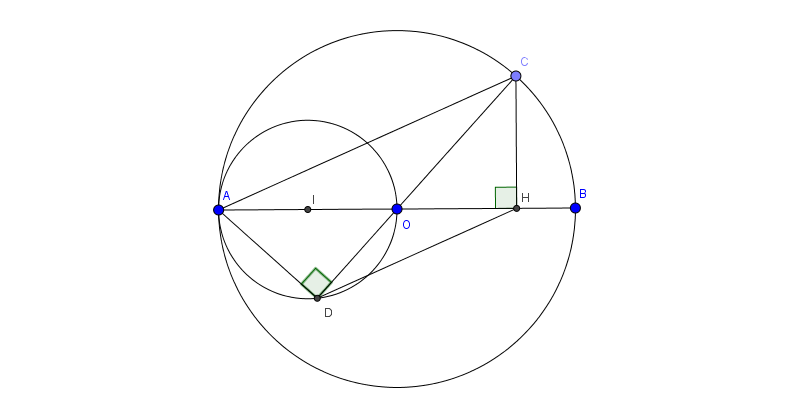
Dễ dàng chứng minh được tam giác ADO vuông tại D. Xét 2 tam giác vuông ADO và CHO có AO=OC; \(\widehat{AOD}=\widehat{COH}\)
\(\Rightarrow \Delta ADO=\Delta CHO\Rightarrow OD=OH; AD=CH\)
\(\Delta DOH\sim \Delta COA\Rightarrow \widehat{OHD}=\widehat{CAO}\Rightarrow DH\parallel AC\) \(\Rightarrow ADHC\) là hình thang cân
Câu 2: Cho đường tròn tâm (O) đường kính AB. H, K lần lượt là hình chiếu vuông góc của A, B lên CD. CM: CH=DK
Hướng dẫn giải
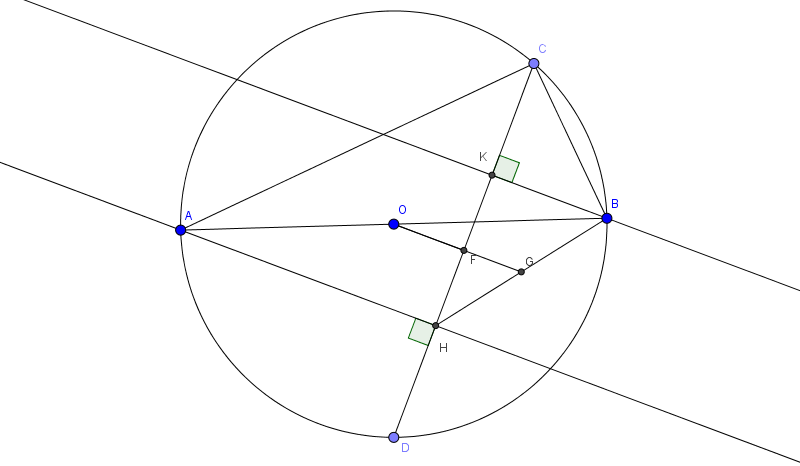
Qua O kẻ đường thẳng vuông góc với CD cắt CD tại F, HB tại G. Xét tam giác ABH có O là trung điểm AB, \(OG\parallel AH\) \(\Rightarrow G\) là trung điểm BH
Xét tam giác HKB có \(FG\parallel KB\) và G là trung điểm BH nên F là trung điểm HK.
mà F là trung điểm CD nên ta có điều phải chứng minh
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho hình chữ nhật ABCD có AD = 12cm, CD = 16cm. Chứng minh rằng bốn điểm ABCD cùng thuộc một đường tròn.Tính bán kính của đường tròn đó.
Câu 2: Cho góc nhọn xOy và hai điểm D, E thuộc tia Oy. Dựng đường tròn tâm M đi qua D và E sao cho tâm M nằm trên tia Ox.
Câu 3: Trong các câu sau, câu nào đúng, câu nào sai?
a. Hai đường tròn phân biệt có thể có hai điểm chung
b. Hai đường tròn phân biệt có thể có ba điểm chung phân biệt
c. Tâm của đường tròn ngoại tiếp một tam giác bao giờ cũng nằm trong tam giác ấy.
Câu 4: Cho hình vuông ABCD, O là giao điểm của hai đường chéo, OA = √2 cm. Vẽ đường tròn tâm A bán kính 2cm. Trong năm điểm A, B, C, D, O, điểm nào nằm trên đường tròn? Điểm nào nằm trong đường tròn? Điểm nào nằm ngoài đường tròn?
3.2. Bài tập trắc nghiệm
Câu 1: Cho hình thang ABCD \((AB\parallel CD), \widehat{C}=\widehat{D}=60^{\circ}, CD=2AD=8\) Khi đó A, B, C, D luôn thuộc đường tròn nào?
A. \((I;R=4\sqrt{2})\) I là trung điểm CD
B. \((O=AC\cap BD;R=4\sqrt{2})\)
C. \((O=AC\cap BD;R=4)\)
D. \((I;R=4)\) I là trung điểm CD
Câu 2: Cho đường tròn tâm A đường kính BC. Gọi D là trung điểm AB. Dây EF vuông góc với AB tại D. Tứ giác EBFA là hình gì?
A. Hình chữ nhật
B. Hình vuông
C. Hình thoi
D. Chưa đủ dữ kiện để kết luận
Câu 3: Cho hai đường thẳng xy và x'y' cuông góc với nhau cắt nhau tại O. Một đoạn thẳng AB=8 chuyển động sao cho A luôn nằm trên xy và B luôn nằm x'y'. Khi đó trung điểm M của AB di chuyển trên đường nào?
A. Đường thẳng song song với xy cách xy 1 đoạn là 4
B. Đường thẳng song song với x'y' cách x'y' 1 đoạn là 4
C. Đường tròn tâm O bán kính là 4
D. Đường tròn tâm O bán kính là 8
Câu 4: Cho tam giác ABC có BH, CE là các đường cao. Gọi M là giao điểm BH và CE. I là trung điểm BC. Khi đó B,C,E,H cùng thuộc đường tròn nào?
A. \((I;R=IA)\)
B. \((I;R=IB)\)
C. \((M;R=MB)\)
D. \((M;R=MA)\)
Câu 5: Cho tam giác ABC nhọn. Đường tròn đường kính BC cắt AB tại N, AC tại M. Gọi H là giao điểm của CN và BM. Khi đó A,N,H,M cùng nằm trên đường tròn nào?
A. \((I;IM)\), I là trung điểm MN
B. \((I;IH)\), I là trung điểm MN
C. \((F;FA)\), F là giao điểm đường tròn với AH
D. \((E;EA)\), E là trung điểm AH
4. Kết luận
Qua bài học này, các em nắm được một số nọi dung chính như sau:
- Nắm được định nghĩa đường tròn, các cách xác định một đườngtròn, đường tròn ngoại tiếp tam giác, tam giác nội tiếp đường tròn. HS nắm đượcđường tròn là hình có tâm đối xứng và trục đối xứng.
- Biết cách dựng dựng đường tròn đi qua điểm không thẳng hàng.Biết chứng minh một điểm nằm trên, nằm bên trong, nằm bên ngoài đường tròn.HS biết vận dụng kiến thức vào thực tế.
Tham khảo thêm
- doc Toán 9 Chương 2 Bài 2: Đường kính và dây của đường tròn
- doc Toán 9 Chương 2 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây
- doc Toán 9 Chương 2 Bài 4: Vị trí tương đối của đường thẳng và đường tròn
- doc Toán 9 Chương 2 Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn
- doc Toán 9 Chương 2 Bài 6: Tính chất của hai tiếp tuyến cắt nhau
- doc Toán 9 Chương 2 Bài 7: Vị trí tương đối của hai đường tròn
- doc Toán 9 Chương 2 Bài 8: Vị trí tương đối của hai đường tròn (tiếp theo)
- doc Toán 9 Ôn tập chương 2: Đường tròn



