Giải bài tập SGK Toán 7 Bài 9: Tính chất ba đường cao của tam giác

Hãy giải thích tại sao trực tâm của tam giác vuông trùng với đỉnh góc vuông và trực tâm của tam giác tù nằm ngoài tam giác.

Hướng dẫn giải

- Trường hợp tam giác \(ABC\) vuông tại \(A\) (hình vẽ) 

- Xét tam giác \(ABC\) vuông tại \(A\) thì \(BA ⊥ CA\) hay \(AB\) là đường cao ứng với cạnh \(AC\) và \(AC\) là đường cao ứng với cạnh \(AB\)

Do đó, \(AB, AC\) là hai đường cao của tam giác \(ABC\) và \(A\) là giao điểm của hai đường cao \(AB\) và \(AC\)

\( \Rightarrow\) \(A\) là trực tâm của tam giác.

Vậy trong tam giác vuông thì trực tâm trùng với đỉnh góc vuông.

- Trường hợp tam giác \(ABC\) có góc A là góc tù, các đường cao \(BK, CP\) và \(AN\) ứng với các cạnh \(AC, AB,BC,\) gọi \(H\) là giao điểm của \(BK\) và \(CP\) (hình vẽ) 

 Giả sử \(P\) nằm giữa \(A\) và \(B\), khi đó

\(\widehat {CAP} \equiv \widehat {CAB}\) là góc tù

Xét \(\Delta ACP\) có \(\widehat {CAP}\) tù (\(\widehat {CAP}>90^0)\); \(\widehat {CPA} = {90^o}\)

Suy ra: \(\widehat {CPA} + \widehat {CAP} > 90^0+90^0\)

Hay  \(\widehat {CPA} + \widehat {CAP} >{180^o}\) (mâu thuẫn với định lí tổng \(3\) góc trong một tam giác)

Do đó \(P\) nằm ngoài \(A\) và \(B\). 

\(⇒\) tia \(CP\) nằm ngoài tia \(CA\) và tia \(CB\)

\(⇒\) tia \(CP\) nằm bên ngoài \(ΔABC.\)

Tương tự ta có tia \(BK\) nằm bên ngoài \(ΔABC.\)

Trực tâm \(H\) là giao của \(BK\) và \(CP ⇒ H\) nằm bên ngoài \(ΔABC.\)

Vậy trực tâm của tam giác tù nằm ở bên ngoài tam giác.

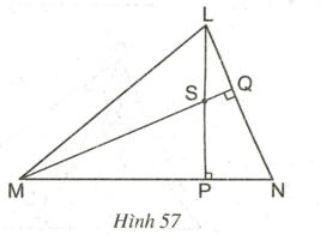
Cho hình \(57\).

a) Chứng minh \(NS ⊥ LM\)

b) Khi \(\widehat{LNP} ={50^0}\), hãy tính góc \(MSP\) và góc \(PSQ.\)

Hướng dẫn giải

Câu a:

Trong \(∆NML\) có: 

\(LP ⊥ MN\) nên \(LP\) là đường cao

\(MQ ⊥ NL\) nên \(MQ\) là đường cao

Mà \(PL\) cắt \(MQ\) tại \(S\)

Suy ra \(S\) là trực tâm của tam giác \(NML\) 

Do đó đường thằng \(NS\) là đường cao kẻ từ \(N\) của tam giác \(NML\) hay \(NS ⊥ LM.\)

Câu b:

\(∆NMQ\) vuông tại \(Q\) và \(\widehat{LNP} ={50^0}\) nên theo định lí tổng ba góc trong của một tam giác ta có:

\(\eqalign{
& \widehat {QMN} = {180^o} - \left( {\widehat {MQN} + \widehat {QNM}} \right) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\; = {180^o} - \left( {{{90}^o} + {{50}^o}} \right) = {40^0} \cr} \)

\( ∆MPS\) vuông tại \(P\) có \(\widehat{QMP} ={40^0}\) nên theo định lí tổng ba góc trong của một tam giác ta có:

\(\eqalign{
& \widehat {MSP} = {180^o} - \left( {\widehat {MPS} + \widehat {SMP}} \right) \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;= {180^o} - \left( {{{90}^o} + {{40}^o}} \right) = {50^0} \cr} \)

Ta có: \(\widehat{MSP} +  \widehat{PSQ} = {180^0}\) (\(2\) góc kề bù)

\( \Rightarrow  \widehat{PSQ}  ={180^0}-\widehat{MSP} \)\(\,= {180^{0}} - {50^0} = {130^0}\)

Trên đường thẳng \(d\), lấy ba điểm phân biệt  \(I, J, K\) (\(J\) ở giữa \(I\) và \(K\))

Kẻ đường thẳng \(l\) vuông góc với \(d\) tại \(J\), trên \(l\) lấy điểm \(M\) khác với điểm \(J\). Đường thẳng qua \(I\) vuông góc với \(MK\) cắt \(l\) tại \(N\). Chứng minh rằng \(KN ⊥ IM.\)

Hướng dẫn giải

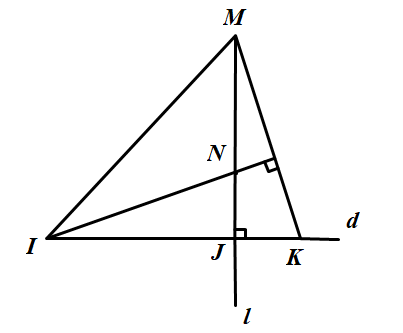
Nối \(M\) với \(I\) ta được \(ΔMIK.\)

Trong \(ΔMIK\) có: \(MJ ⊥ IK\) (do \(l ⊥ d\)) và \(IN ⊥ MK\) (giả thiết)

Nên \(MJ,IN\) là hai đường cao của \(ΔMIK.\)

Mà \(MJ\) và \(IN\) cắt nhau tại \(N\) nên \(N\) là trực tâm của \(ΔMIK.\)

Suy ra \(KN\) là đường cao thứ ba của \(ΔMIK\) hay \(KN ⊥ IM\) (điều phải chứng minh).

Cho tam giác \(ABC\) không vuông. Gọi \(H\) là trực tâm của nó.

a) Hãy chỉ ra các đường cao của tam giác \(HBC.\) Từ đó hãy chỉ ta trực tâm của tam giác đó.

b) Tương tự, hãy lần lượt chỉ ra trực tâm của các tam giác \(HAB, HAC.\)

Hướng dẫn giải

Các đường thẳng \(HA, HB, HC\) lần lượt cắt cạnh đối \(BC, AC, AB\) tại \(N, M, E.\)

Câu a: \(∆HBC\) có:

\(HN ⊥ BC\) nên \(HN\) là đường cao

\(BE ⊥ HC\) nên \(BE\) là đường cao

\(CM ⊥ BH\) nên \(CM\) là đường cao

Mà \(A\) là giao điểm của các đường thẳng \(HN, BE, CM\) nên \(A\) là trực tâm của \(∆HBC\).

Câu b: \(∆AHB\) có:

\(HE \bot AB \) nên \(HE\) là đường cao

\(BC \bot AH \) nên \(BC\) là đường cao

\(AC \bot BH\) nên \(AC\) là đường cao

Mà \(C\) là giao điểm của các đường \(HE, BC, AC\) nên \(C\) là trực tâm của \(∆AHB\)

\( ∆AHC\) có: 

\(HM \bot AC\) nên \(HM\) là đường cao

\(AB \bot HC \) nên \(AB\) là đường cao

\(CB \bot AH \) nên \(CB\) là đường cao

Mà \(B\) là giao điểm của các đường \(HM,AB,CB\) nên \(B\) là trực tâm của \( ∆AHC\).

Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.

Hướng dẫn giải

- TH1: Xét ΔABC vuông tại A có các đường cao AD, BA, CA.

BA, CA là hai đường cao xuất phát từ hai góc nhọn B và C của ΔABC.

AB = AC ⇒ ΔABC cân tại A (đpcm).

- TH2: Xét ΔABC không có góc nào vuông, hai đường cao BD = CE (như hình vẽ minh họa)

Xét hai tam giác vuông EBC và DCB có :

BC (cạnh chung)

CE = BD (giả thiết)

⇒ ∆EBC = ∆DCB (cạnh huyền - cạnh góc vuông)

Suy ra \(\widehat {EBC} = \widehat {DCB}\) (hai góc tương ứng)

Hay \(\widehat {ABC} = \widehat {ACB} \Rightarrow \Delta ABC\) cân tại A.

Xét ΔABC ba đường cao BD = CE = AF (như hình vẽ minh họa)

CE = BD ⇒ ΔABC cân tại A (như cmt) ⇒ AB = AC.

CE = AF ⇒ ΔABC cân tại B (như cmt) ⇒ AB = BC:

⇒ AB = AC = BC

⇒ ΔABC đều.