Giải bài tập SGK Toán 7 Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu

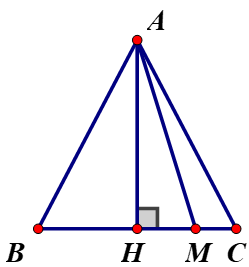
Cho hình 11, biết rằng \(AB < AC\). Trong các kết luận sau kết luận nào đúng? Tại sao?

a) \(HB = HC\).

b) \(HB > HC\).

c) \(HB < HC\).

Phương pháp giải

Áp dụng quan hệ giữa đường xiên và hình chiếu: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó: Đường xiên nào lớn hơn thì có hình chiếu lớn hơn.

Ở đây ta so sánh các hình chiếu có đường xiên kẻ từ điểm M đến đường thẳng BC.

Hướng dẫn giải

\(AB, AC\) là hai đường xiên kẻ từ \(A\) đến \(BC\).

\(AH \bot BC\) nên \(HB\) là hình chiếu của \(AB\) trên \(BC\); \(HC\) là hình chiếu của \(AC\) trên \(BC\).

Vì \(AB < AC\) (giả thiết) nên \(HB < HC\) ( đường xiên nào lớn hơn thì có hình chiếu lớn hơn). 

Vậy kết luận C đúng.

Để tập bơi nâng dần khoảng cách, hàng ngày bạn Nam xuất phát từ \(M\), ngày thứ nhất bạn bơi đến \(A\), ngày thứ hai bạn bơi đến \(B\), ngày thứ ba bạn bơi đến \(C\) ...(hình 12).

Hỏi rằng bạn Nam tập bơi như thế có đúng mục đích đề ra hay không (ngày hôm sau có bơi xa hơn ngày hôm trước hay không)? Vì sao?

Phương pháp giải

Áp dụng quan hệ giữa đường xiên và hình chiếu: Trong các đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó: Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.

Ở đây ta so sánh các hình chiếu có đường xiên kẻ từ điểm M đến đường thẳng AD.

Hướng dẫn giải

Theo hình vẽ các điểm \(A, B, C, D\) nằm trên một đường thẳng (ta gọi là đường thẳng \(d \)) và điểm \(M\) nằm ngoài đường thẳng đó. \(MA\) là đường vuông góc kẻ từ \(M\) đến đường thẳng \(d\). Các đoạn thẳng \(MB, MC, MD\) là các đường xiên kẻ từ \(M\) lần lượt đến \(B, C\) và \(D\).

Ta có \(AB, AC, AD\) lần lượt là hình chiếu của \(MB, MC, MD\) xuống \(d\).

Từ hình vẽ ta có \( AD > AC > AB \) suy ra \(MD > MC >MB \) (Theo định lí 2: đường xiên nào có hình chiếu lớn hơn thì lớn hơn)    (1)

Theo định lí 1 đường vuông góc là đường ngắn nhất nên \(MA

Từ (1) và (2) suy ra: \(MD > MC >MB >MA\).

Điều đó có nghĩa là ngày hôm sau bạn Nam bơi được xa hơn ngày hôm trước, tức là bạn Nam tập đúng mục đích đề ra.

Chứng minh rằng trong một tam giác cân, độ dài đoạn thẳng nối đỉnh đối diện với đáy và một điểm bất kỳ của cạnh đáy nhỏ hơn hoặc bằng độ dài của cạnh bên.

Phương pháp giải

Áp dụng quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó: Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.

Ở đây ta so sánh các hình chiếu có đường xiên kẻ từ điểm A đến đường thẳng BC.

Hướng dẫn giải

Giả sử \(∆ABC\) cân tại \(A\), \(M\) là điểm thuộc cạnh đáy \(BC\), ta chứng minh \(AM ≤ AB; AM ≤ AC\).

- Nếu \(M  ≡ B\) hoặc \(M  ≡  C\) ( Kí hiệu \(≡\) đọc là trùng với) thì \(AM = AB, AM = AC\).

- Nếu \(M\) nằm giữa \(B\) và \(C\); ( \(M\) khác  \(B , C\)). Gọi \(H\) là trung điểm của \(BC\), mà \(∆ABC\) cân tại \(A\) nên \(AH ⊥ BC\).

• Nếu \(M ≡ H\) \(\Rightarrow \) \(AM ⊥ BC\) \(\Rightarrow \) \(AM < AB\) và \(AM < AC\) (đường vuông góc luôn nhỏ hơn đường xiên) 
• Nếu \(M\) \(\not\equiv\)  \(H\), giả sử \(M\) nằm giữa \(H\) và \(C\) \(\Rightarrow \) \(MH < CH\).

Vì \(MH\) và \(CH\) lần lượt là hình chiếu của \(MA\) và \(CA\) trên đường thẳng \(BC\) nên \(MH < CH\)\(\Rightarrow MA < CA\) (Theo định lí 2: đường xiên nào có hình chiếu lớn hơn thì lớn hơn)

Mà \(CA=BA\) \(\Rightarrow \) \(MA < BA\).

Chứng minh tương tự nếu \(M\) nằm giữa \(H\) và \(B\) thì \(MA < AB, MA < AC\)

Vậy mọi vị trí của \(M\) trên cạnh đáy \(BC\) thì \(AM ≤  AB, AM ≤  AC\).

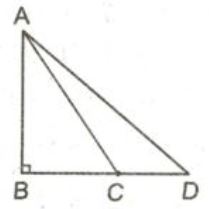
Cho hình \(13\): Dùng quan hệ giữa góc và cạnh đối diện trong một tam giác để chứng minh rằng: 

 Nếu \(BC < BD\) thì \(AC < AD\)

Hướng dẫn:

a) Góc \(ACD\) là góc gì? Tại sao?

b) Trong tam giác \(ACD\), cạnh nào lớn nhất, tại sao?

Phương pháp giải

- Áp dụng quan hệ giữa cạnh và góc đối diện trong tam giác: Trong một tam giác, cạnh đối diện góc lớn hơn thì lớn hơn.

- Áp dụng quan hệ giữa đường xiên và hình chiếu: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó: Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.

Hướng dẫn giải

Câu a:

\(\widehat{ACD}\) là góc ngoài tại \(C\) của  \(∆ABC\) nên \(\widehat{ACD}=\widehat{ABC}+\widehat{BAC}\) 

Do đó \(\widehat{ACD}> \widehat{ABC}\).

Mà \(\widehat {ABC} = {90^o}\) tức là \(\widehat{ACD}>{90^o}\) hay \(\widehat{ACD}\) là góc tù.

Câu b:

Trong tam giác \(ACD\) có \(\widehat{ACD}\) là góc tù

Mà AD là cạnh đối diện với góc ACD.

Suy ra AD là cạnh lớn nhất trong tam giác ACD (cạnh đối diện với góc tù là cạnh lớn nhất trong tam giác).

Nên AD > AC hay AC < AD

Vậy Nếu : BC < BD thì AC < AD.

Cho hình \(a\). Ta gọi độ dài đoạn thẳng \(AB\) là khoảng cách giữa hai đường thẳng song song \(a\) và \(b\).

Một tấm gỗ xẻ có hai cạnh song song. Chiều rộng của tấm gỗ là khoảng cách giữa hai cạnh đó

Muốn đo chiều rộng của tấm gỗ, ta phải đặt thước như thế nào? Tại sao? Cách đặt thước như trong hình \(b\) có đúng không?

Phương pháp giải

- Khoảng cách giữa hai đường thẳng song song là độ dài đoạn vuông góc vẽ từ một điểm nằm trên đường thẳng này đến đường thẳng kia.

- Áp dụng quan hệ giữa đường xiên và hình chiếu: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó: Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.

Hướng dẫn giải

Trong bài này ta được khái niệm mới là khoảng cách giữa hai đường thẳng song song là độ dài đoạn vuông góc vẽ từ một điểm nằm trên đường thẳng này đến đường thẳng kia. Vì vậy muốn đo bề rộng của tấm gỗ chính là xác định khoảng cách giữa hai đường thẳng song song ta phải đặt thước vuông góc với một trong hai cạnh song song của tấm gỗ. Cách đặt thước như trong hình là sai.

Cho hình 16. Hãy chứng minh rằng:

a) \(BE < BC\)

b) \(DE < BC\)

Phương pháp giải

- Áp dụng quan hệ giữa cạnh và góc đối diện trong tam giác: Trong một tam giác, cạnh đối diện góc lớn hơn thì lớn hơn.

- Áp dụng quan hệ giữa đường xiên và hình chiếu: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó: Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.

Hướng dẫn giải

Câu a:

Trong hình vẽ \(BE\) và \(BC\) là hai đường xiên vẽ từ \(B\) đến đường \(AC\) và \(AE, AC\) lần lượt là hai hình chiếu của \(BE; \,BC\).  

Vì \(AE < AC\) (vì E nằm giữa A và C) nên \(BE < BC\) (đường xiên nào có hình chiếu lớn hơn thì lớn hơn). 

Câu b:

Vì \(EA \bot AB\) nên \(EB\) và \(ED\) là hai đường xiên vẽ từ \(E\) đến \(AB\) và \(AB, AD\) lần lượt là hai hình chiếu của \(EB;\;ED\).

Vì \(AD < AB\) (vì D nằm giữa A và B) nên \(DE < BE\) (đường xiên nào có hình chiếu lớn hơn thì lớn hơn)

Ta có: \(BE < BC\) (câu a) và \(DE <  BE\) nên \(DE < BC\).

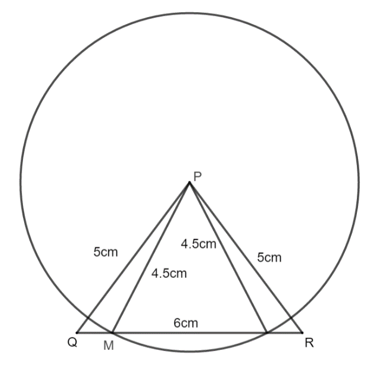
Đố : Vẽ tam giác \(PQR\) có \(PQ = PR =5\,cm\), \(QR = 6\,cm\). Lấy điểm \(M\) trên đường thẳng \(QR\) sao cho \(PM = 4,5\,cm\). Có mấy điểm \(M\) như vậy ?

Điểm \(M\) có nằm trên cạnh \(QR\) hay không? Tại sao ?

Phương pháp giải

- Tìm các tam giác bằng nhau để chứng minh các cạnh bằng nhau.

- Áp dụng định lý Py-ta-go cho tam giác vuông để tính các cạnh chưa biết.

- Áp dụngquan hệ giữa đường xiên và hình chiếu: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó:

• Đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
• Đường xiên nào lớn hơn thì có hình chiếu lớn hơn.

Hướng dẫn giải

Vẽ hình:

- Vẽ tam giác \(PQR\) có \(PQ = PR = 5\,cm,\; QR = 6\,cm\).

• Vẽ đoạn thẳng \(QR = 6\,cm\).
• Vẽ cung tròn tâm \(Q\) và cung tròn tâm \(R\) bán kính \(5\,cm\). Hai cung tròn này cắt nhau tại \(P\).
• Nối \(PQ\) và \(PR\) ta được tam giác cần vẽ.

- Vẽ điểm \(M\): Vẽ cung tròn tâm \(P\) bán kính \(4,5\,cm\) cắt đường thẳng \(QR\) (nếu có) tại \(M\).

Chứng minh 

\(∆PQR\) có \(PQ = PR = 5\,cm\) nên \(∆PQR\) cân tại \(P\). Từ \(P\) kẻ đường thẳng \(PH ⊥ QR\).

Xét hai tam giác vuông tại H: \(ΔPHQ\) và \(ΔPHR\) có

\(PH\) chung

\(PQ = PR ( = 5cm)\)

\(⇒ ΔPHQ = ΔPHR\) (cạnh huyền – cạnh góc vuông)

\(⇒ HQ = HR\) (Hai cạnh tương ứng)

Mà \(HQ + HR = QR = 6 cm\)

Suy ra \(HQ=HR=QR:2=6:2=3cm\)

\(ΔPHR\) vuông tại H có \(PR^2= PH^2+ HR^2\) (định lí Py – ta – go)

\(⇒ PH^2= PR^2– HR^2= 5^2– 3^2= 16\)\( ⇒ PH = 4cm .\)

Đường vuông góc \(PH = 4cm\) là đường ngắn nhất trong các đường kẻ P đến đường thẳng QR.

Vậy chắc chắn có đường xiên \(PM = 4,5cm\) (vì \(PM = 4,5cm > 4cm)\) kẻ từ P đến đường thẳng QR.

Gọi \(M\) là một điểm nằm trên đường thẳng \(QR\).

Ta có: \(MH, QH, RH\) lần lượt là hình chiếu của \(PM, PQ, PR\) trên \(QR\).

Vì \(PM = 4,5\,cm < PQ\) (hoặc \(PR\)) nên \(MH < QH, MH < RH\).

- Trên đoạn thẳng \(QH\) có \(MH < QH\) nên \(M\) nằm giữa hai điểm \(Q\) và \(H\).

- Tương tự trên \(RH \) có \(MH < RH\) nên \(M\) nằm giữa hai điểm \(R\) và \(H\).

Do vậy có hai điểm \(M\) thỏa mãn điều kiện đề bài và điểm \(M\) này nằm trên cạnh \(QR\).