Giải bài tập SGK Toán 7 Bài 7: Đồ thị hàm số y = ax (a # 0)

Vẽ trên cùng một hệ trục toạ độ \(Oxy\) đồ thị của các hàm số:

a) \(y = x\);

b) \(y = 3x\);

c) \(y = -2x\);

d) \(y = -x\).

Phương pháp giải

Đồ thị hàm số \( y = ax \left( {a \ne 0} \right)\) là một đường thẳng đi qua gốc tọa độ.

- Ta lấy \(x\ne0\) bất kỳ tìm \(y\) để tìm được tọa độ điểm thứ \(2\) gọi là điểm \(A\) mà đồ thị đó đi qua.

- Vẽ đường thẳng đi qua điểm \(O\) và \(A\) ta được đồ thị cần tìm.

Hướng dẫn giải

Câu a: \(y = x\)

- Vẽ hệ trục tọa độ \(Oxy\)

- Cho \(x = 0\) được \(y = 0\) \(\Rightarrow O (0; 0)\) thuộc đồ thị hàm số \(y=x\).

- Cho \(x = 2\) được \(y = 2\) \(\Rightarrow A (2; 2)\) thuộc đồ thị hàm số \(y=x\).

Vậy đường thẳng \(OA\) là đồ thị của hàm số đã cho.

Câu b: \(y = 3x\)

- Vẽ hệ trục tọa độ \(Oxy\)

- Cho \(x = 0\) được \(y = 0\) \(\Rightarrow O (0; 0)\) thuộc đồ thị hàm số \(y=3x\).

- Cho \(x = 1\) được \(y = 3\) \(\Rightarrow B (1; 3)\) thuộc đồ thị hàm số \(y=3x\).

Vậy đường thẳng \(OB\) là đồ thị của hàm số đã cho.

Câu c: \(y = -2x\)

- Vẽ hệ trục tọa độ \(Oxy\)

- Cho \(x = 0\) được \(y = 0\). Điểm \(O (0; 0)\) thuộc đồ thị của hàm số  \(y = -2x\).

- Cho \(x = -1\) được \(y = 2\). Điểm \(C (-1; 2)\) thuộc đồ thị của hàm số  \(y = -2x\).

Vậy đường thẳng \(OC\) là đồ thị của hàm số đã cho.

Câu d: 

\(y = -x\)

- Vẽ hệ trục tọa độ \(Oxy\)

- Cho \(x = 0\) được \(y = 0\). Điểm \(O (0; 0)\) thuộc đồ thị của hàm số  \(y = -x\).

- Cho \(x = 1\) được \(y = -1\). Điểm \(D (1; -1)\) thuộc đồ thị của hàm số  \(y = -x\).

Vậy đường thẳng \(OD\) là đồ thị của hàm số đã cho.

Ta có đồ thị như sau:

Đồ thị của hàm số \(y = ax\) nằm ở những góc phần tư nào của mặt phẳng toạ độ \(Oxy\), nếu:

a) \(a > 0?\)

b) \(a < 0?\)

Phương pháp giải

Để dễ hình dung ta vẽ \(2\) trường hợp với \(a > 0\) và \(a<0\) trong trường hợp tổng quát rồi nhận xét.

Hướng dẫn giải

Câu a: Khi \(a > 0\) đồ thị hàm số \(y = ax\) nằm ở góc phần tư \(I\) và \(III.\)

Câu b: Khi \(a < 0\) đồ thị hàm số \(y = ax\) nằm ở góc phần tư thứ \(II\) và \(IV.\)

Những điểm nào sau đây thuộc đồ thị hàm số \(y = -3x.\)

\(A\left( { - \dfrac{1}{3};1} \right);\,\,B\left( { - \dfrac{1}{3}; - 1} \right);\,C\left( {0;0} \right)\)

Phương pháp giải

Để kiểm tra xem các điểm \(A, B, C\) có thuộc đồ thị hàm số hay không ta thay hoành độ của từng điểm vào công thức hàm số, sau đó tìm được kết quả \(y\) đối chiếu với tung độ của điểm đó, nếu trùng nhau thì điểm đó thuộc vào đồ thị hàm số đã cho.

Hướng dẫn giải

Ta có: \( y = -3x \)

- Với \(A\left( { - \dfrac{1}{3};1} \right)\) ta thay \(x =  - \dfrac{1}{3}\) vào công thức hàm số ta được:

\(y =  - 3.\left( { - \dfrac{1}{3}} \right) = 1\) nên điểm \(A\) thuộc đồ thị hàm số \(y = -3x.\)

- Với \(B\left( { - \dfrac{1}{3}; - 1} \right)\) ta thay \(x =  - \dfrac{1}{3}\) vào công thức hàm số ta được:

\(y =  - 3.\left( { - \dfrac{1}{3}} \right) = 1 \ne  - 1\) nên điểm \(B\) không thuộc đồ thị hàm số \(y = -3x.\)

- Với \( C (0; 0) \) ta thay \(x = 0\) vào công thức hàm số ta được: \(y = -3.0 = 0 \) nên điểm \(C \) thuộc đồ thị hàm số \(y = -3x.\)

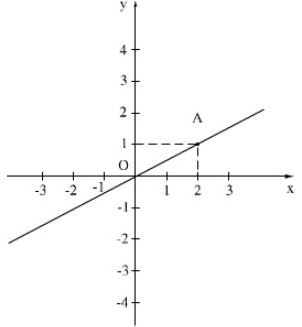
Đường thẳng \(OA\) trong hình 26 là đồ thị của hàm số \(y = ax.\)

a) Hãy xác định hệ số \(a.\)

b) Đánh dấu điểm trên đồ thị có hoành độ bằng \(\dfrac{1}{2}\) ;

c) Đánh dấu điểm trên đồ thị có tung độ bằng \(-1\).  

Phương pháp giải

a) Để xác định hệ số \(a\), ta thay tọa độ điểm \(A (2;1)\) vào hàm số ban đầu sau đó tìm được \(a.\)

b) Đánh dấu điểm trên đồ thị có hoành độ bằng \(m\): Từ \(x = m\) vẽ đường vuông góc với \(Ox\). Giao điểm của đường vuông góc vừa vẽ với đồ thị là điểm cần xác định.

c) Đánh dấu điểm trên đồ thị có tung độ bằng \(n\): Từ \(y=n\) vẽ đường vuông góc với \(Oy\). Giao điểm của đường vuông góc vừa vẽ với đồ thị là điểm cần xác định. 

Hướng dẫn giải

Câu a: Theo hình vẽ ta có: \(A\left( {2;1} \right)\) thuộc vào đồ thị hàm số \(y = ax \)

Ta thay \( x = 2; y = 1\) vào hàm số \(y = ax\) ta được: 

\(1 = a.2\Rightarrow  a = \dfrac{1}{2}\)

Từ đó ta tìm được hàm số: \(y = \dfrac{1}{2}x\)

Câu b: Điểm trên đồ thị có hoành độ bằng \(\dfrac{1}{2}\).

Với \(x = \dfrac{1}{2}\) thay vào hàm số: \(y = \dfrac{1}{2}x\) ta có: \(y = \dfrac{1}{2}. \dfrac{1}{2}= \dfrac{1}{4}\).

Vậy điểm cần biểu diễn là \(B\left( {\dfrac{1}{2};\dfrac{1}{4}} \right)\)

Cách xác định điểm trên đồ thị có hoành độ bằng \(\dfrac{1}{2}:\)

Từ \(x = \dfrac{1}{2}\) vẽ đường vuông góc với \(Ox\). Giao điểm của đường vuông góc vừa vẽ với \(OA\) là điểm cần xác định.

(Hoặc ta chỉ cần biểu diễn điểm \(B\left( {\dfrac{1}{2};\dfrac{1}{4}} \right)\) trên mặt phẳng tọa độ) 

Câu c: Với điểm có tung độ bằng \(-1\) thì ta thay \(y= -1\) vào hàm số \(y = \dfrac{1}{2}x\) ta được:

\(-1=\dfrac{1}{2}.x\Rightarrow x= -2\)

Điểm trên đồ thị có tung độ bằng \(-1\) là điểm \(C(-2;-1)\) .

- Cách xác định điểm trên đồ thị có tung độ bằng \(-1\):

Từ \(y=-1\) vẽ đường vuông góc với \(Oy\). Giao điểm của đường vuông góc vừa vẽ với \(OA\) là điểm cần xác định. 

(Hoặc ta chỉ cần biểu diễn điểm \(C(-2;-1)\) trên mặt phẳng tọa độ) 

Trong hình 27: Đoạn thẳng \(OA\) là đồ thị biểu diễn chuyển động của người đi bộ và đoạn thẳng \(OB\) là đồ thị biểu diễn chuyển động của người đi xe đạp. Mỗi đơn vị trên trục \(Ot\) biểu thị một giờ, mỗi đơn vị trên trục \(OS\) biểu thị mười kilômét. Qua đồ thị, em hãy cho biết:

a) Thời gian chuyển động của người đi bộ, của người đi xe đạp.

b) Quãng đường đi được của người đi bộ, của người đi xe đạp.

c) Vận tốc (km/h) của người đi bộ, của người đi xe đạp.

Phương pháp giải

Áp dụng công thức tính vận tốc là: \(v = \dfrac{s}{t}\)

Hướng dẫn giải

Câu a: Thời gian chuyển động của người đi bộ là \(t_1=4\) giờ, của người đi xe đạp là \(t_2=2\) giờ.

Câu b: Quãng đường đi được của người đi bộ là \(s_1=2.10=20\, km\), của người đi xe đạp là \(s_2=3.10=30\, km.\)

Câu c: Ta có công thức tính vận tốc là : \(v = \dfrac{s}{t}\)

- Vận tốc của người đi bộ là: 

\({v_1} = \dfrac{{{s_1}}}{{{t_1}}} = \dfrac{{20}}{4} = 5\,\,(km/h)\)

- Vận tốc của người đi xe đạp là: 

\({v_2} = \dfrac{{{s_2}}}{{{t_2}}} = \dfrac{{30}}{2} = 15\,\,(km/h)\)

Vẽ đồ thị của hàm số \(y =f(x) = -0,5x.\) Bằng đồ thị hãy tìm:

a) \(f(2); f(-2); f(4); f(0)\)

b) Giá trị của \(x\) khi \(y = -1; y = 0; y = 2,5.\)

c) Các giá trị của \(x\) khi \(y\) dương, khi \(y\) âm.

Phương pháp giải

Đồ thị hàm số \( y = ax \left( {a \ne 0} \right)\) là một đường thẳng đi qua gốc tọa độ.

- Ta lấy \(x\ne0\) bất kỳ tìm \(y\) để tìm được tọa độ điểm thứ \(2\) gọi là điểm \(A\) mà đồ thị đó đi qua.

- Vẽ đường thẳng đi qua điểm \(O\) và \(A\) ta được đồ thị cần tìm.

Hướng dẫn giải

Vẽ đồ thị hàm số \(y =f(x) = -0,5x.\)

Cho \(x = 2\) được \(y = -1\) \( \Rightarrow A(2;-1)\) thuộc đồ thị \(y =f(x) = -0,5x.\)

Vậy đường thẳng \(OA\) là đồ thị của hàm số đã cho.

Câu a: Từ đồ thị hàm số ta có:

\(f(2)=-1;f(-2)= 1\); \(f(4) = -2\); \(f(0)= 0\)

(Cách xác định như sau:

Để tìm \(f(2)\): Từ hoành độ \(x=2\) ta vẽ đường vuông góc với \(Ox\), đường vuông góc này cắt đồ thị tại đâu thì từ điểm đó vẽ đường vuông góc với \(Oy\), giao điểm với \(Oy\) là giá trị của \(y=f(2)=-1\).

Bằng cách đó ta xác định được các giá trị còn lại của \(f(x)\)) 

Câu b: Từ đồ thị hàm số ta có:

Khi \(y = -1 \) thì \( x = 2\)

Khi \(y = 0  \) thì \( x = 0\)

Khi \(y = 2,5  \) thì \(  x = -5\)

(Cách xác định như sau:

Với \(y=-1\), từ tung độ \(y=-1\) ta vẽ đường vuông góc với \(Oy\), đường vuông góc này cắt đồ thị tại đâu thì từ điểm đó ta vẽ đường vuông góc với \(Ox\), giao điểm với \(Ox\) là giá trị \(x=2\).

Bằng cách đó ta xác định được các giá trị của \(x\)) 

Câu c: Các giá trị của \(x\) khi \(y\) dương, khi \(y\) âm.

Từ đồ thị đã cho ta thấy khi \(y\) dương thì đồ thị nằm ở góc phần tư thứ \(II\), các điểm thuộc đồ thị có hoành độ âm (nhỏ hơn không).

Vậy khi \(y\) dương thì \(x\) có giá trị âm.

Tương tự khi \(y\) âm thì đồ thị nằm ở góc phần tư thứ \(IV\), các điểm thuộc đồ thị có hoành độ dương.

Vậy khi \(y\) âm thì \(x\) có giá trị dương.

Hai cạnh của hình chữ nhật có độ dài là \(3\,m\) và \(x\) (m).

Hãy viết công thức biểu diễn diện tích \(y\; ({m^2})\) theo \(x.\)

Vì sao đại lượng \(y\) là hàm số của đại lượng \(x?\)

Hãy vẽ đồ thị của hàm số đó.

Xem đồ thị, hãy cho biết:

a) Diện tích của hình chữ nhật bằng bao nhiêu khi \(x = 3m; x = 4 m?\)

b) Cạnh \(x\) bằng bao nhiêu khi diện tích \(y\) của hình chữ nhật bằng \(6 \,{m^2} ; 9 \,{m^2}?\)

Phương pháp giải

- Áp dụng công thức tính diện tích hình chữ nhật:

\(S=ab\)

Trong đó: \(S\) là diện tích; \(a;b\) là độ dài hai cạnh hình chữ nhật.

- Nếu đại lượng \(y\) phụ thuộc vào đại lượng thay đổi \(x\) sao cho với mỗi giá trị của \(x\) ta luôn xác định được chỉ một giá trị tương ứng của \(y\) thì \(y\) được gọi là hàm số của \(x\).

Hướng dẫn giải

Công thức biểu diễn diện tích \(y\) theo \(x\) là \(y = 3x\)

Vì với mỗi giá trị của \(x\) ta xác định được chỉ một giá trị tương ứng của \(y\) nên đại lượng \(y\) là hàm số của đại lượng \(x.\)

Vẽ đồ thị hàm số: 

Cho \(x = 1\) được \(y = 3\) \( \Rightarrow  A(1;3)\) thuộc đồ thị.

Đồ thị hàm số là đường thẳng đi qua \(2\) điểm \(O\) và \(A.\)

Vẽ đồ thị:

Câu a: Trên đồ thị thấy:

\(x = 3  \Rightarrow  y = 9.\)

Vậy khi \(x = 3\,m\) thì diện tích hình chữ nhật bằng \(9 ({m^2})\)

\(x = 4  \Rightarrow  y = 12 .\)

Vậy khi \(x = 4\,m\) thì diện tích hình chữ nhật bằng \(12 ({m^2})\)

Câu b: Từ đồ thị, ta có: 

\(y = 6 \Rightarrow  x = 2.\)

Vậy khi diện tích hình chữ nhật bằng \(6\;m^2\) thì cạnh \(x = 2\; (m).\)

\(y = 9 \Rightarrow x = 3.\)

Vậy diện tích hình chữ nhật bằng \(9\;m^2\) thì cạnh \(x = 3\; (m)\)

Đồ thị trong hình 28 được sử dụng để đổi đơn vị độ dài in – sơ sang xentimet.

Xem đồ thị hãy cho biết \(2\) in (in – sơ), \(3\) in (in – sơ),  bằng khoảng bao nhiêu xen ti mét?

Phương pháp giải

Từ điểm \(3\) trên trục hoành dựng đường thẳng song song với trục tung cắt đồ thị tại một điểm. Từ điểm đó ta dựng đường song song với trục hoành cắt trục tung tại một điểm. Điểm này chính là số xen ti mét ứng với \(3\) in.

Hướng dẫn giải

\(2\) in \(≈ 5,08\) cm 

\(3\) in \(≈ 7,5\) cm

Đường thẳng \(OA\) trên hình \(29\) là đồ thị của hàm số \(y = ax.\) Hệ số \(a\) bằng bao nhiêu?

Phương pháp giải

Để tìm được hệ số \(a\) thì ta thay tọa độ của điểm \(A(-3;1)\) vào hàm số \(y=ax\) từ đó ta tìm được \(a\).

Hướng dẫn giải

Từ hình vẽ, ta có hàm số \(y = ax\) có đồ thị là đường thẳng qua điểm \(A(-3;1)\).

Thay tọa độ của điểm \(A\) vào công thức hàm số \(y=ax\) ta có:

\(1 = a. (-3)\) \(\Rightarrow a =  - \dfrac{1}{3}\).

Vậy hệ số \( a =  - \dfrac{1}{3}\).