Toán 8 Chương 4 Bài 8: Diện tích xung quanh của hình chóp đều

Ta thường sử dụng các công thức sau:

- Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy và trung đoạn.

\({S_{xq}} = p.d\) (p là nửa chu vi đáy; d là trung đoạn của hình chóp đều).

- Diện tích toàn phần của hình chop bằng tổng của diện tích xung quanh và diện tích đáy.

- Với hình chóp, để tính diện tích xung quanh ta tính tổng diện tích của các mặt bên.

- Để tính diện tích xung quanh của hình chóp cụt đều, ta tính diện tích một mặt bên rồi nhân với số mặt bên, hoặc lấy diện tích xung quanh của hình chóp đều lớn trừ đi diện tích xung quanh của hình chóp đều nhỏ.

Một hình chóp tứ giác đều có độ dài cạnh đáy là 6cm, chiều cao là 4cm thì diện tích xung quanh là?

Hướng dẫn giải

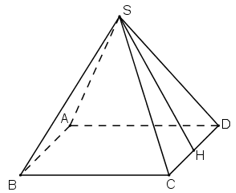
Giả sử có chóp đều \(S.ABCD\), \(O\) là tâm của đáy, \(I\) là trung điểm của \(CD\).

Áp dụng định lí Py-ta-go vào tam giác vuông \(SOI\), ta có:

\(S{I^2} = S{O^2} + O{I^2}\)

\(\Rightarrow SI = \sqrt {S{O^2} + O{I^2}}\)\(\,  = \sqrt {{4^2} + {3^2}}  = 5\,\left( {cm} \right)\)

Diện tích xung quanh của hình chóp là:

\(\displaystyle {S_{xq}} = {1 \over 2}.4.6.5 = 60\;(c{m^2})\)

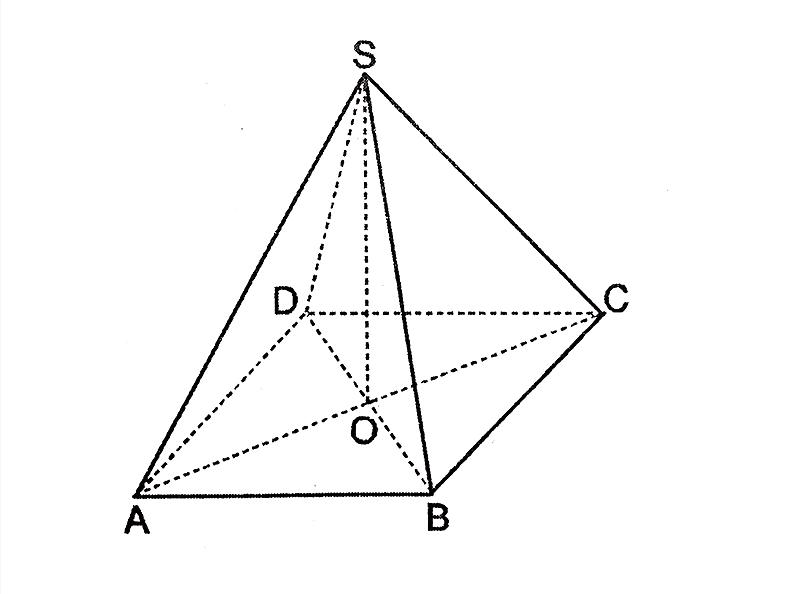
Một hình chóp tứ giác đều có độ dài cạnh bên bằng \(25cm\), đáy là hình vuông \(ABCD\) cạnh \(30cm\).

Tính diện tích toàn phần của hình chóp.

Hướng dẫn giải

Gọi \(H\) là trung điểm của \(BC\). 

Khi đó ta có: \(BH = HC = \dfrac{1}{2}BC =\dfrac{1}{2}. 30=15 \,cm  \)

Vì tam giác \(SBC\) cân tại \(S\) nên \( SH\perp BC \).

Ta có:  \(d = SH = \sqrt{SB^2- BH^2}\) \( = \sqrt{25^2 -15^2} = \sqrt{400}=20(cm)\) 

Chu vi đáy là: \(4. 30 = 120 (cm)\)

Diện tích xung quanh của hình chóp:

\(S_{xq} = p.d =\dfrac{1}{2} .120.20 = 1200 (cm^2) \) 

Diện tích đáy là:  

\( S_{đ} = 30.30 = 900 (cm^2)\)

Diện tích toàn phần của hình chóp là:

\( S_{tp} =S_{xq}+ S_{đ} = 1200 + 900 \) \(= 2100 (cm^2) \)

Câu 1: Tính diện tích toàn phần của hình chóp tam giác đều theo các kích thước trên hình vẽ.

Câu 2: Một hình chóp tứ giác đều có độ dài cạnh đáy là \(6cm\), chiều cao là \(4cm\) thì diện tích xung quanh là?

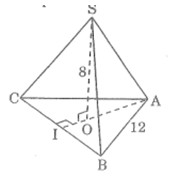
Câu 3: Hình chóp đều \(S.ABC\) có cạnh đáy \(a = 12cm\), chiều cao \(h = 8cm.\) Hãy tính diện tích xung quanh của hình chóp đó.

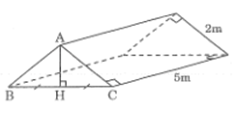
Câu 4: Hình vẽ là chiếc lều ở một trại hè với các kích thước trên hình ABC là tam giác vuông cân.

a) Tính thể tích lều.

b) Số vải bạt cần có để dựng lều đó là bao nhiêu?

Câu 1: Một hình chóp tứ giác đều có diện tích xung quanh là \(30cm^{2}\), trung đoạn của 5cm. Độ dài cạnh đáy là:

A. 6cm

B. 12cm

C. 3cm

D. 1,5cm

Câu 2: Cho hình chóp tam giác đều S.ABC có diện tích toàn phần là \(25\sqrt{3}\) . SB=x. Ta có:

A. x=5

B. x=25

C. x=2,5 

D. x=\(5\sqrt{3}\)

Câu 3: Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính diện tích toàn phần của hình chóp:

A. \(a^{2}\sqrt{3}\)

B. \(2a^{2}\)

C. \(a^{2}(\sqrt{3}+1)\)

D. \(2a^{2}\sqrt{3}\)

Câu 4: Một tứ diện đều có cạnh bằng 2, có diện tích toàn phần bằng bao nhiêu?

A. 8

B. 16

C. \(4\sqrt{6}\)

D. \(4\sqrt{3}\)

Câu 5: Bốn đỉnh của một hình lập phương của đỉnh một hình chóp tam giác đều. Tìm tỉ số diện tích toàn phần của hình lập phương và diện tích toàn phần của hình chóp tam giác đều.

A. \(\sqrt{2}\)

B. \(\sqrt{3}\)

C. \(\sqrt{\frac{3}{2}}\)

D. \(\frac{2}{\sqrt{3}}\)

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Nắm được cách tính diện tích xung quanh hình chóp đều
• Biết áp dụng công thức tính toán đối với các hình cụ thể, hoàn thiện dần kỷ năng gấp hình, củng cố các khái niệm hình học đã học