Toán 8 Chương 4 Bài 3: Thể tích của hình hộp chữ nhật

a) Đường thẳng vuông góc với mặt phẳng

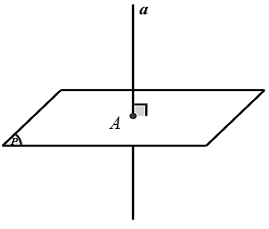
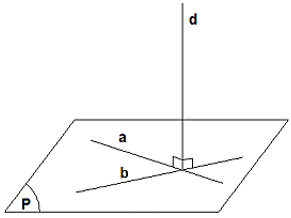
– Đường thẳng d gọi là vuông góc với mặt phẳng ( P ) nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng ( P ). Kí hiệu d ⊥ ( P ).

– Nếu một đường thẳng a vuông góc với mặt phẳng ( P ) tại điểm A thì nó vuông góc với mọi đường thẳng nằm trong ( P ) và đi qua điểm A.

b) Hai mặt phẳng vuông góc

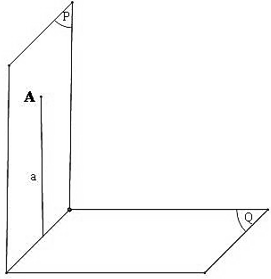
– Mặt phẳng ( P ) gọi là vuông góc với mặt phẳng ( Q ) nếu mặt phẳng ( P ) chứa đường thẳng vuông góc với mặt phẳng ( Q ). Kí hiệu ( Q ) ⊥ ( P ).

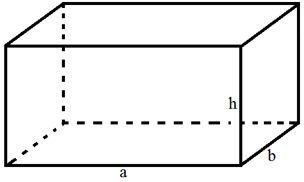
a) Thể tích hình hộp chữ nhật

Ta có V = a.b.h

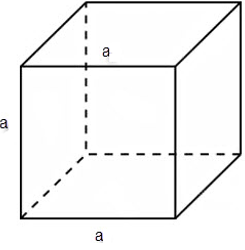
b) Thể thích hình lập phương

Ta có: V = a³

a) Tính các kích thước của một hình hộp chữ nhật, biết rằng chúng tỉ lệ với \(3,\, 4,\, 5\) và thể tích của hình hộp này là \(480 cm^3\).

b) Diện tích toàn phần của một hình lập phương là \(486 m^2\). Thể tích của nó bằng bao nhiêu?

Hướng dẫn giải

a) Gọi \(a,\, b,\, c\) là ba kích thước của hình hộp chữ nhật.

Vì \(a,\, b,\, c\) tỉ lệ với \(3,\, 4,\, 5\) nên

\(\dfrac{a}{3} = \dfrac{b}{4} = \dfrac{c}{5}= t \;  ( t > 0)   \) 

\(\Rightarrow  a = 3t;\; b = 4t;\; c = 5t  \quad (1) \)

Mà thể tích hình hộp là \( 480cm^3\) nên \(a.b.c = 480 \quad  (2)\)

Từ (1) và (2) suy ra 

\( 3t.4t.5t = 480 \Rightarrow 60t^3 = 480\)

\(  \Rightarrow t^3 = 8 \Rightarrow t = 2 \) 

Do đó:

\(a =3t=3.2= 6(cm);\\ b=4t=4.2 = 8(cm); \\ c=5t=5.2 = 10 (cm) \)

Vậy các kích thước của hình hộp là \(6cm;\; 8cm; \; 10cm\) .

b) Hình lập phương là hình có \( 6\) mặt là các hình vuông bằng nhau.

Diện tích một mặt là: \(486 : 6 = 81 (cm^2) \)

Gọi \(a\) là độ dài cạnh hình lập phương, ta có: \(a^2=81\)

Suy ra độ dài cạnh hình lập phương là  \( a = \sqrt{81}=9\, (cm) \).

Thể tích hình lập phương là :    \( V = a^3 = 9^3 = 729 (cm^3)  \).

Một bể nước hình hộp chữ nhật có chiều dài \(2m\). Lúc đầu bể không có nước. Sau khi đổ vào bể \(120\) thùng nước, mỗi thùng chứa \(20\) lít thì mực nước của bể cao \(0,8m\).

a) Tính chiều rộng của bể nước.

b) Người ta đổ thêm vào bể \(60\) thùng nước nữa thì đầy bể. Hỏi bể cao bao nhiêu mét?

Hướng dẫn giải

a) Thể tích nước đổ vào là: \(120 . 20 = 2400 (l) =2400dm^3= 2,4\) \((m^3) \)

Chiều rộng của bể nước là: \(2,4 : (2 . 0,8) = 1,5 (m)\)

b) Thể tích nước đổ thêm vào bể là: \(60 . 20 = 1200 (l) =1200dm^3= 1,2\) \((m^3) \) 

Thể tích của bể nước là: \(2,4 +1,2 = 3,6(m^3) \)

Chiều cao của bể nước là: \(3,6 : (2 . 1,5) = 1,2(m) \).

Câu 1: Từ một đoạn dây thép ngắn hơn \(1,5m\), liệu người ta có thể tạo ra một cái khung hình lập phương có cạnh là \(1dm\) được hay không? (đoạn dây thép để nguyên, không cắt).

Câu 2: Từ một tờ giấy hình vuông kích thước \(3 × 3\) liệu có thể gấp để tạo thành một hình lập phương đơn vị hay không? (có thể làm nắp rời)

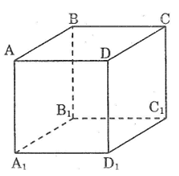
Câu 3: Tìm trên hình hộp chữ nhật \(ABCD.{A_1}{B_1}{C_1}{D_1}\) một ví dụ cụ thể để chứng tỏ mệnh đề sau là sai

Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.

Câu 4: Một cái thùng hình lập phương, cạnh \(7dm\), có chứa nước với độ sâu của nước là \(4dm\). Người ta thả \(25\) viên gạch có chiều dài \(2dm\), chiều rộng \(1dm\) và chiều cao \(0,5dm\) vào thùng. Hỏi nước trong thùng dâng lên cách miệng thùng bao nhiêu đề-xi-mét? (Giả thiết toàn bộ gạch ngập trong nước và chúng hút nước không đáng kể).