Toán 7 Chương 2 Bài 6: Tam giác cân

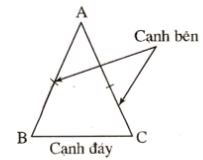
Tam giác cân là tam giác có hai cạnh bằng nhau.

Ví dụ: Xét tam giác ABC có AB = AC nên tam giác ABC cân tại A.

Trong một tam giác cân hai góc ở đáy bằng nhau.

• Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân
• Tam giác vuông cân là tam giác vuông hai cạnh góc vuông bằng nhau.

Ví dụ: Xét tam giác ABC có \(\widehat B = \widehat C\) nên tam giác ABC cân tại A.

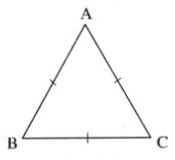
Định nghĩa: Tam giác đều là tam giác có ba cạnh bằng nhau.

Ví dụ: Tam giác ABC đều có AB = AC = BC.

Hệ quả:

• Trong tam giác đều, mỗi góc bằng  \({60^0}\)
• Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.
• Nếu một tam giác cân có một góc bằng \({60^0}\) thì tam giác đó là tam giác đều.

Ví dụ: 

• Tam giác ABC đều có \(\widehat A = \widehat B = \widehat C = 60^\circ \)
• Tam giác ABC có \(\widehat A = \widehat B = \widehat C\) thì tam giác ABC là tam giác đều.
• Tam giác ABC cân có \(\widehat A =60^\circ \) thì tam giác ABC đều.

Câu 1: Cho tam giác ABC cân tại A có \(\widehat A = {50^0}\)

a. Tính \(\widehat B,\,\,\widehat C\)

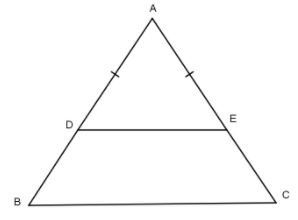
b. Lấy điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho AD = AE. Chứng minh rằng DE // BC.

Hướng dẫn giải

a. Ta có:

\(\begin{array}{l}\widehat B = \,\,\widehat C = \frac{{{{180}^0} - \widehat A}}{2} = \frac{{{{180}^0} - {{50}^0}}}{2}\\ = \widehat B = \,\,\widehat C = {65^0}\,{\,^{(1)}}\end{array}\)

b. AD = AE nên \(\Delta ADE\) cận tại A

Suy ra \(\,\widehat {ADE} = \frac{{{{180}^0} - \widehat A}}{2} = \frac{{{{180}^0} - {{50}^0}}}{2} = {65^0}\,{\,^{(2)}}\)

Từ (1) và (2) suy ra \(\widehat B = \widehat {ADE}\)

Vậy DE // BC (hai góc đồng vị bằng nhau)

Câu 2: Cho tam giác cân tại A. Gọi D là trung điểm của AC, gọi E là trung điểm của AB. So sánh các độ dài BD và CE.

Hướng dẫn giải

Xem hình vẽ:

Cách 1: \(\Delta ABD\) và \(\Delta ACE\) có:

AB = AC (gt)

\(\widehat A\) chung

Nên \(\Delta ABD = \Delta ACE\,\,(c.g.c)\)

Suy ra BD = CE.

Cách 2: \(\Delta BDC\) và \(\Delta CEB\) có

CD = BE (gt)

\(\widehat B = \widehat {C\,}\,(gt)\)

BC cạnh chung

Nên \(\Delta BDC = \Delta CEB\,\,\,(c.g.c)\)

Suy ra BD = CE

Câu 3: Cho \(\Delta ABC\) cân tại A và có \(\widehat B = 2\widehat A\) phân giác của góc B cắt AC tại D.

a. Tính các góc của \(\Delta ABC\)

b. Chứng minh DA = DB

c. Chứng minh DA = BC

Hướng dẫn giải

a. Ta có \(\widehat {A\,} + \widehat {B\,} + \widehat {C\,} = {180^0}\)

mà \(\Delta ABC\)cân tại A, có \(\widehat B = 2\widehat A\), nên:

\(\widehat {A\,} + 2\widehat {A\,} + \widehat {A\,} = {180^0}\)

Thay \(5\widehat {A\,} = {180^0} \Rightarrow \widehat {A\,} = {36^0}\)

Nên \(\widehat {B\,} = \widehat {C\,} = 2\widehat {A\,} = {72^0}\)

b. Ta có: \(\widehat {DBA} = \frac{1}{2}\widehat B = {36^0}\) (BD phân giác \(\widehat B\))

mà \(\widehat {A\,} = {36^0}\) nên \(\widehat {A\,} = \widehat {DBA}\)

Suy ra \(\Delta ABD\) cân tại D

Vậy \(DA = DB{\,^{\,(1)}}\)

c. Ta có: \(\widehat {BDC}\) là góc ngoài tại D của \(\Delta ABD\) nên

\(\widehat {BDC} = \widehat {DBA} + \widehat A = {36^0} + {36^0} = {72^0}\)

Mà \(\widehat C = {72^0}\) suy ra \(\Delta DBC\) cân tại B

Nên BD = BC (2)

Từ (1) và (2) suy ra AD = BC.

Câu 1: Cho  hai đường thẳng x’x và y’y song song và một đường thẳng cắt x’x tại M và y’y tại N. Trên đường thẳng y’y lấy hai điểm E, F ở về hai phía của N sao cho NE=NF=NM. Chứng minh:

a. ME, MF là hai tia phân giác của hai góc \(\widehat {xMN}\) và \(\widehat {x'MN}\)

b. \(\Delta M{\rm{EF}}\) là tam giác vuông

Câu 2: Cho tam giác cân ABC (AB=AC) trên tia đối của tia BC lấy điểm D và trên tia đối của tia CB lấy điểm E sao cho CE = BD. Nếu A với D và A với E.

a. So sánh \(\widehat {ABD}\) và \(\widehat {ACE}\)

b. Chứng minh \(\Delta ADE\) cân.

Câu 3: Cho \(\Delta ABD,\,\widehat B = 2\widehat D\), kẻ \(AH \bot BD\,\;(H \in BD)\)

Trên tia đối của tia BA lấy BE = BH. Đường thẳng EH cắt ED tại F. Chứng minh: FH = FA = FD.

Câu 1: Chọn câu sai:

A. Tam giác đều có ba góc bằng nhau và bằng 60⁰

B. Tam giác đều có ba cạnh bằng nhau 

C. Tam giác cân là tam giác đều 

D. Tam giác đều là tam giác cân

Câu 2: Hai góc nhọn của tam giác vuông cân bằng nhau và bằng:

A. 30⁰

B. 45⁰

C. 60⁰

D. 90⁰

Câu 3: Cho tam giác ABC cân tại A. Phát biểu nào trong các phát biểu sau là sai:

A. \(\widehat B = \widehat C\)

B. \(\widehat C = \frac{{{{180}^0} - \widehat A}}{2}\)

C. \(\widehat A = {180^0} - 2\widehat C\)

D. \(\widehat B \ne \widehat C\)

Câu 4: Một tam giác cân có góc ở đỉnh bằng 64⁰ thì số đo góc ở đáy là:

A. 54⁰

B. 58⁰

C. 72⁰

D. 90⁰

Câu 5: Một tam giác cân có góc ở đáy bằng 70⁰ thì số đo góc ở đỉnh là:

A. 54⁰

B. 63⁰

C. 70⁰

D. 40⁰

Qua bài học này, các em cần đạt được những mục tiêu sau:

• Định nghĩa, tính chất tam giác cân.

• Định nghĩa, tính chất tam giác đều.