Giải bài tập SGK Vật lý 12 nâng cao Bài 6: Dao động điều hòa

Tốc độ của chất điểm dao động điều hoà cực đại khi

A. Li độ cực đại. 

B. Gia tốc cực đại.                  

C. Li độ bằng 0.

D. pha bằng π/4.

Phương pháp giải

- Dựa vào hệ thức độc lập:

\({\left( {\frac{x}{A}} \right)^2} + {\left( {\frac{v}{{A\omega }}} \right)^2} = 1\)

- Cho x = 0, ta có v= Aω =v_max

Hướng dẫn giải

- Giữa li độ và vận tốc v có công thức liên hệ:

\({\left( {\frac{x}{A}} \right)^2} + {\left( {\frac{v}{{A\omega }}} \right)^2} = 1\)

- Cho x = 0, ta có v= Aω =v_max

⇒ Tốc độ của chất điểm dao động điều hoà cực đại khi li độ bằng 0. 

- Chọn đáp án C. 

Gia tốc của chất điểm dao động điều hoà bằng 0 khi

A. Li độ cực đại.

B. Li độ cực tiểu.

C. Vận tốc cực đại hoặc cực tiểu.

D. Vận tốc bằng 0.

Phương pháp giải

- Dựa vào công thức tính gia tốc: 

a = xω²

⇒ khi x = 0 thì a bằng 0

- Ở VTCB vận tốc đại cực đại hoặc cực tiểu 

Hướng dẫn giải

- Gia tốc của chất điểm dao động điều hòa: 

a = xω²

+ a = amax khi x = A (ở biên)

+ a =0 khi x=0 (VTCB)

- Ở VTCB vận tốc đại cực đại hoặc cực tiểu

- Gia tốc chất diểm dao động điều hoà bằng 0 khi vận tốc cực đại hoặc cực tiểu.

- Chọn đáp án C. 

Dao động điều hoà đổi chiều khi

A. Lực tác dụng đổi chiều.                                          

B. Lực tác dụng bằng 0.

C. Lực tác dụng có độ lớn cực đại.                             

D. Lực tác dụng có độ lớn cực tiểu.

Phương pháp giải

- Dựa vào công thức tính lực phục hồi:

F=−kx và F_max = kA

- Ta thấy, dao động đổi chiều khi lực tác dụng có độ lớn cực đại.

Hướng dẫn giải

- Lực phục hồi  F=−kx lớn nhất khi vật ở vị trí biên F_max = kA, lúc đó vật dao động đổi chiều để chuyển động ngược lại.

⇒ Dao động cơ điều hoà, đổi chiều khi lực tác dụng có độ lớn cực đại.

- Chọn đáp án C.

a) Thử lại rằng :x=A₁cosωt+A₂sinωt (6.14) trong đó A₁ và A₂ là hai hằng số bất kì cũng là nghiệm của phương trình (6.3).

b) Chứng tỏ rằng, nếu chọn A₁ và A₂ trong  biểu thức ở vế trái của (6.14) như sau: A₁=Acosφ; A₂=−Asinφ thì biểu thức ấy trùng với biểu thức ở vế phải của (6.4).

Phương pháp giải

a)- Lấy đạo hàm cấp 2 của phương trình x, ta được:

\(x'' = - {A_1}{\omega ^2}\cos \omega t - {A_2}{\omega ^2}\sin \omega t.\)

- Cho x"+ω²x=0 giải phương trình ta được:

x=A1cosωt+A₂sinωt

b) Chọn A₁=Acosφ và A₂=−Asinφ ta được

\({ x = Acos\left( {\omega t + \varphi } \right).}\)

Hướng dẫn giải

a) Ta có :

\(\begin{array}{l} x = {A_1}\cos \omega t + {A_2}\sin \omega t\\ \Rightarrow x' = - {A_1}\omega \sin \omega t + {A_2}\omega \cos \omega t. \end{array}\)

\(x'' = - {A_1}{\omega ^2}\cos \omega t - {A_2}{\omega ^2}\sin \omega t.\)

Ta được:

\(\begin{array}{l} x'' + {\omega ^2}x\\ = - {A_1}{\omega ^2}\cos \omega t - {A_2}{\omega ^2}sin\omega t + {\omega ^2}({A_1}\cos \omega t + {A_2}\sin \omega t) \end{array}\)

\(\begin{array}{l} \Rightarrow x'' + {\omega ^2}x\\ = - {A_1}{\omega ^2}\cos \omega t - {A_2}{\omega ^2}sin\omega t + {A_1}{\omega ^2}\cos \omega t + {A_2}{\omega ^2}sin\omega t\\ = 0. \end{array}\)

Vậy:

x=A1cosωt+A₂sinωt là nghiệm của phương trình x"+ω²x=0..

b) Nếu chọn A₁=Acosφ và A₂=−Asinφ thì  

\({x = {A_1}\cos \omega t + {A_2}\sin \omega t = A\cos \varphi cos\omega t - A\sin \varphi \sin \omega t}\)

\({ = A(\cos \varphi cos\omega t - \sin \varphi \sin \omega t)}\)

\({ \Rightarrow x = Acos\left( {\omega t + \varphi } \right).}\)

Phương trình dao động của một vật là:

x=6cos(4πt+π/6)(cm).

a) Xác định biên độ, tần số góc, chu kì và tần số của dao dộng.

b) Xác định pha của dao động tại thời điểm t=14s, từ đó suy ra li độ tại thời điểm ấy.

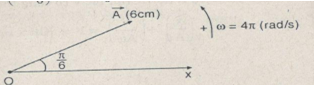
c) Vẽ vectơ quay biểu diễn dao động tại thời điểm t=0.

Phương pháp giải

a) Dựa theo phương trình dao động để xác định biên độ A, tần số góc ω

⇒ Tính chu kì và tần số bằng công thức:

T=2π/ω và f = 1/T

b) Thay t=14 vào pha dao động của phương trình, ta được: x=−3√3

c) Biểu diễn như hình vẽ bên dưới

Hướng dẫn giải

Phương trình dao động của vật:

x=6cos(4πt+π/6)(cm)

a) Biên độ A=6 (cm)

- Chu kì:

T=2π/ω=2π/4π=0,5(s)

- Tần só góc ω=4π(rad/s)

- Tần số:

f=1/T=10,5=2(Hz)

b) Khi t=14(s)

⇒pha(ωt+φ)=(4π.14+π/6)=7π6

⇒x=6cos(π+π/6)=−6cosπ/6=−6.√3/2=−3√3(cm).

c) Vẽ vectơ quay biểu diễn dao động vào thời điểm t=0: