Giải bài tập SGK Vật lý 12 nâng cao Bài 12: Tổng hợp dao động
Nội dung hướng dẫn Giải bài tập Lý 12 nâng cao Bài 12 dưới đây sẽ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức về tổng hợp dap động. Mời các em cùng theo dõi.
Mục lục nội dung

1. Giải bài 1 trang 60 SGK Vật lý 12 nâng cao
Xét dao động tổng hợp của hai dao động hợp thành có cùng phương và cùng tần số. Biên độ của dao động tổng hợp không phụ thuộc
A. Biên độ của dao động hợp thành thứ nhất.
B. Biên độ của dao động hợp thành thứ hai.
C. Tần số chung của hai dao động hợp thành.
D. Độ lệch pha của hai dao động hợp thành.
Phương pháp giải
Dựa vào biểu thức:
\({A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos ({\varphi _2} - {\varphi _1})\)
Hướng dẫn giải
- Biên độ của dao động tổng hợp không phụ thuộc tần số chung của hai dao động hợp thành
- Chọn đáp án C.
2. Giải bài 2 trang 60 SGK Vật lý 12 nâng cao
Hai dao động cơ điều hoà cùng phương, cùng tần số góc ω=50rad/s, có biên độ lần lượt là 100mm và 173mm, dao động thứ hai trễ pha π/2 so với dao động thứ nhất. Xác định dao động tổng hợp.
Hướng dẫn : Có thể chọn gốc thời gian so với pha ban đầu của dao động thứ nhất bằng 0.
Phương pháp giải
- Cách 1: giải bằng phương pháp vectơ quay
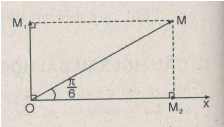
Tính đoạn OM và tanφ= OM1/OM2 theo hình vẽ cách 1
- Cách 2: cho dao động thứ hai trễ pha π/2 so với dao động thứ nhất
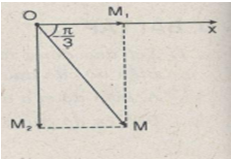
Tương tự, tính đoạn OM và tanφ= OM1/OM2 theo hình vẽ cách 2
Hướng dẫn giải
- Cách 1:
+ Chọn gốc thời gian sao cho pha ban đầu của dao động thứ hai bằng 0 thì dao động thứ nhất sẽ sớm pha hơn dao động thứ hai một góc π/2.
⇒ x1=100cos(50t+π/2)(mm); x2=173cos50t(mm)
+ Ta có thể giải bằng phương pháp vectơ quay.
\(\begin{array}{l} OM = \sqrt {OM_1^2 + OM_2^2} \\ = \sqrt {{{100}^2} + {{173}^2}} \approx 200(mm)\\ \tan \varphi = \frac{{O{M_1}}}{{O{M_2}}} = \frac{{100}}{{173}} = 0,578 \Rightarrow \varphi = \frac{\pi }{6} \end{array}\)
Vậy x=200cos(50t+π/6)(mm)
- Cách 2:
+ Ta có thể cho dao động thứ hai trễ pha π/2 so với dao động thứ nhất 1 góc π/2 thì :
\(\begin{array}{l} {x_1} = 100\cos 50t(mm);\\ {x_2} = 173\cos \left( {50t - \frac{\pi }{2}} \right)(mm)\\ OM = \sqrt {OM_1^2 + OM_2^2} = 200(mm) \end{array}\)
+ Và:
\(\begin{array}{l} \tan \varphi = - \frac{{O{M_2}}}{{O{M_1}}} = - 1,73\\ \Rightarrow \varphi = - \frac{\pi }{3} \end{array}\)
Vậy: x=200cos(50t−π/3)(mm)
3. Giải bài 3 trang 60 SGK Vật lý 12 nâng cao
Dùng công thức lượng giác (tổng của hai cosin) tìm tổng hợp của hai dao động điều hoà cùng phương, cùng tần số góc ω, cùng biên độ A và có độ lệch pha Δφ. Đối chiếu với kết quả nhận được bằng phương pháp sử dụng giản đồ Fre - nen.
Phương pháp giải
Khi dùng công thức lượng giác hay giản đồ Fre-nen, ta đều nhận được:
- Biên độ dao động là:
\( A = 2Acos\frac{{\Delta \varphi }}{2}\)
- Pha dao động:
\( \varphi = \frac{{{\varphi _1} + {\varphi _2}}}{2}\)
Hướng dẫn giải
- Tổng của hai dao động của hai dao động điều hoà cùng phương, cùng tần số góc ω, cùng biên độ A và có độ lệch pha Δφ=φ2−φ1.
\({{x_1} = A\cos (\omega t + {\varphi _1});{x_2} = A\cos (\omega t + {\varphi _2})}\)
\({ \Rightarrow x = {x_1} + {x_2} = A\cos (\omega t + {\varphi _1}) + A\cos (\omega t + {\varphi _2})}\)
\({ = A\left[ {\cos (\omega t + {\varphi _1}) + \cos (\omega t + {\varphi _2})} \right]}\)
\({ = 2A\cos \frac{{\omega t + {\varphi _1} + \omega t + {\varphi _2}}}{2}\cos \frac{{\omega t + {\varphi _1} - \omega t - {\varphi _2}}}{2}}\)
- Biên độ của dao động tổng hợp là 2AcosΔφ/2
- Pha ban đầu của dao động tổng hợp:
φ=(φ1+φ2)/2
- Đối chiếu khi dùng phương pháp giản đồ Fre-nen thì :
\(\begin{array}{*{20}{l}} {{A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}cos({\varphi _1} - {\varphi _2})}\\ \begin{array}{l} = {A^2} + {A^2} + 2{A^2}cos\Delta \varphi \\ = 2{A^2}(1 + cos\Delta \varphi ) \end{array}\\ \begin{array}{l} = 2{A^2}.2co{s^2}\frac{{\Delta \varphi }}{2}\\ = 4{A^2}co{s^2}\frac{{\Delta \varphi }}{2} \end{array}\\ { \Rightarrow A = 2Acos\frac{{\Delta \varphi }}{2}.} \end{array}\)
- Mặt khác:
\(\begin{array}{*{20}{l}} {tan\varphi = \frac{{{A_1}sin{\varphi _1} + {A_2}sin{\varphi _2}}}{{{A_1}cos{\varphi _1} + {A_2}cos{\varphi _2}}}}\\ \begin{array}{l} = \frac{{Asin{\varphi _1} + Asin{\varphi _2}}}{{Acos{\varphi _1} + Acos{\varphi _2}}}\\ = \frac{{sin{\varphi _1} + sin{\varphi _2}}}{{cos{\varphi _1} + cos{\varphi _2}}} \end{array}\\ \begin{array}{l} = \frac{{2sin\frac{{{\varphi _1} + {\varphi _2}}}{2}cos\frac{{{\varphi _1} - {\varphi _2}}}{2}}}{{2cos\frac{{{\varphi _1} + {\varphi _2}}}{2}cos\frac{{{\varphi _1} - {\varphi _2}}}{2}}}\\ = tan\frac{{{\varphi _1} + {\varphi _2}}}{2} \end{array}\\ { \Rightarrow \varphi = \frac{{{\varphi _1} + {\varphi _2}}}{2}} \end{array}\)
Tham khảo thêm
- doc Giải bài tập SGK Vật lý 12 nâng cao Bài 6: Dao động điều hòa
- doc Giải bài tập SGK Vật lý 12 nâng cao Bài 7: Con lắc đơn - Con lắc vật lý
- doc Giải bài tập SGK Vật lý 12 nâng cao Bài 8: Năng lượng trong dao động điều hòa
- doc Giải bài tập SGK Vật lý 12 nâng cao Bài 10: Dao động tắt dần và dao động duy trì
- doc Giải bài tập SGK Vật lý 12 nâng cao Bài 11: Dao động cưỡng bức - cộng hưởng
- doc Giải bài tập SGK Vật lý 12 nâng cao Bài 13: TH xác định chu kì dao động của con lắc đơn hoặc con lắc lò xo và gia tốc trọng trường



