Giải bài tập SGK Vật lý 12 nâng cao Bài 8: Năng lượng trong dao động điều hòa

Động năng của vật nặng dao động điều hoà biến đổi theo thời gian

A. Theo một hàm dạng sin.                                         

B. Tuần hoàn với chu kì T.

C. Tuần hoàn với chu kì T/2.                                        

D. Không đổi.

Phương pháp giải

Trong dao động điều hòa, chu kì của động năng bằng 1/2 lần chu kì của vật

Hướng dẫn giải

- Động năng của vật nặng dao động điều hoà biến đổi theo thời gian tuần hoàn với chu kì T/2.

- Chọn đáp án C.

Một vật có khối lượng 750 g dao động điều hoà với biên độ 4 cm và chu kì T=2. Tính năng lượng của dao động.  

Phương pháp giải

Áp dụng công thức tính năng lượng:

\(W = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}m{\left( {\frac{{2\pi }}{T}} \right)^2}{A^2}\)

Hướng dẫn giải

- Vật dao động điều hoà có:

m= 750(g)= 0,75(kg), A=4 (cm), T=2 (s). 

- Năng lượng của dao động:

\(\begin{array}{l} W = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}m{\left( {\frac{{2\pi }}{T}} \right)^2}{A^2}\\ \Rightarrow W = \frac{1}{2}.0,75.{\left( {\frac{{2\pi }}{2}} \right)^2}.{(0,04)^2} = 0,006(J) \end{array}\)

Tính thế năng, động năng và cơ năng của con lắc đơn ở một vị trí bất kì (li độ góc α) và thử lại rằng cơ năng không đổi trong chuyển động.

Phương pháp giải

a) Áp dụng công thức tính thế năng:

\(\Rightarrow {W_t} = \frac{1}{2}m\frac{g}{\ell }{s^2} = \frac{1}{2}m{\omega ^2}{s^2}\)

b) Áp dụng công thức tính động năng:

\({W_d} = \frac{1}{2}m{\omega ^2}(s_0^2 - {s^2}).\)

c) Áp dụng công thức tính cơ năng:

\(W = \frac{1}{2}m{\omega ^2}s_0^2\)

Hướng dẫn giải

Xét con lắc đơn, ở một vị trí bất kì (có li độ góc α):

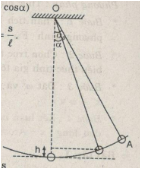
a) Biểu thức thế năng :    

W_t= mgh= mgℓ(1−cosα)

- Với dao động nhỏ:

1−cosα=α/2; α=sℓ

- Thay vào  

\(\Rightarrow {W_t} = \frac{1}{2}m\frac{g}{\ell }{s^2} = \frac{1}{2}m{\omega ^2}{s^2}\)                         

b) Biểu thức động năng:

W_đ= 1/2mv²

với v²= 2gℓ(cosα−cosα₀).

- Dao động nhỏ :

1−cosα=α²/2; 1−cosα₀= α_o²/2 và α= sℓ.

- Thay vào ta được:

\({W_d} = \frac{1}{2}m{\omega ^2}(s_0^2 - {s^2}).\)

c) Cơ năng:

\(\begin{array}{l} W = {W_d} + {W_t}\\ = \frac{1}{2}m{\omega ^2}(s_0^2 - {s^2}) - \frac{1}{2}m{\omega ^2}{s^2}\\ \Rightarrow W = \frac{1}{2}m{\omega ^2}s_0^2 \end{array}\)

không đổi trong chuyển động.

Dựa vào định luật bảo toàn cơ năng, tính :

a) Vận tốc của vật nặng trong con lắc lò xo khi đi qua vị trí cân bằng theo biên độ A.

b) Vận tốc của con lắc đơn khi đi qua vị trí cân bằng theo biên độ góc α₀.

Phương pháp giải

a) Áp dụng công thức:

\(W = {W_{_{d\max }}} = \frac{1}{2}mv_{\max }^2\\\)

để tìm vận tốc:

\(v = \pm A\omega\)

b) Áp dụng công thức:

\(W = {W_d} = \frac{1}{2}m{\omega ^2}s_0^2 = \frac{1}{2}m{v^2}\)

để tìm vận tốc:

\(v = \pm \omega {s_0} = \pm \sqrt {2gl(1 - \cos {\alpha _0})}\)

Hướng dẫn giải

Dựa vào định luật bảo toàn cơ năng, ta tính được :

a) Vận tốc của vật nặng trong con lắc lò xo khi đi qua vị trí cân bằng :

\(\begin{array}{l} x = 0\\ \Rightarrow {{\rm{W}}_t} = 0\\ \Rightarrow W = {W_{_{d\max }}} = \frac{1}{2}mv_{\max }^2\\ \Rightarrow W = \frac{1}{2}m{(v)^2} = \frac{1}{2}m{(\omega A)^2} \Rightarrow v = \pm A\omega . \end{array}\)

b) Vận tốc con lắc đơn khi đi qua vị trí cân bằng theo biên độ góc α₀

\(\begin{array}{l} \alpha = 0\\ \Rightarrow {W_t} = 0\\ W = {W_d} \Leftrightarrow \frac{1}{2}m{\omega ^2}s_0^2 = \frac{1}{2}m{v^2}\\ \Rightarrow v = \pm \omega {s_0} = \pm \sqrt {2gl(1 - \cos {\alpha _0})} \end{array}\)