Giải bài tập SGK Toán 9 Bài 4: Vị trí tương đối của đường thẳng và đường tròn

Điền vào các chỗ trống (...) trong bảng sau (R là bán kính của đường tròn, d là khoảng cách từ tâm đến đường thẳng):

Phương pháp giải

Cho đường thẳng a và đường tròn (O). Kẻ \(OH\bot a\), đặt \(OH=d\).

\(-\) Nếu \(d< R\) thì a và đường tròn (O) cắt nhau.

Hướng dẫn giải

Từ hệ thức giữa d và R ta có bảng:

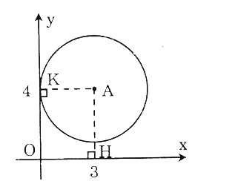
Trên mặt phẳng tọa độ Oxy, cho điểm \(A(3; 4)\). Hãy xác định vị trí tương đối của đường tròn \((A; 3)\) và các trục tọa độ.

Phương pháp giải

Cho đường tròn \((O;R)\), gọi d là khoảng cách từ đường tròn tâm O đến đường thẳng 

+ Nếu d = R thì \(\Delta\) tiếp xúc với đường tròn (O);

+ Nếu d < R thì \(\Delta\) cắt (O);

+ Nếu d > R thì \(\Delta\) và (O) không giao nhau.

Hướng dẫn giải

Kẻ \(AH ⊥ Ox, AK ⊥ Oy\).

Vì \(AH=y_A = 4 > R = 3\) nên đường tròn tâm (A) và trục hoành không giao nhau.

Vì \(AK=x_A = 3 = R\) nên đường tròn (A) và trục tung tiếp xúc nhau.

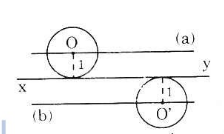
Cho đường thẳng xy. Tâm của các đường tròn có bán kính 1cm và tiếp xúc với đường thẳng xy nằm trên đường nào?

Phương pháp giải

- Xác định xem tâm đường tròn cách đường thẳng cho trước một khoảng là bao nhiêu.

- Vận dụng tính chất: Tập hợp các điểm cách đường thẳng \(d\) một khoảng \(a(cm)\) là đường thẳng song song với \(d\) và cách \(d\) là \(a(cm)\).

Hướng dẫn giải

Gọi O là tâm của một đường tròn bất kì có bán kính bằng 1cm và tiếp xúc với đường thẳng xy.

Ta có: \(R = 1\), và đường tròn tiếp xúc với đường thẳng xy nên ta có: \(d = R\), suy ra \(d = 1\)

\(\Rightarrow \) Tâm O cách đường thẳng xy một khoảng cố định 1cm nên nằm trên các đường thẳng (a) và (b) song song với xy và cách xy một khoảng là 1cm.

Cho đường tròn tâm O bán kính 6cm và một điểm A cách O là 10cm. Kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Tính độ dài AB.

Phương pháp giải

Áp dụng định lí Pytago trong tam giác vuông OAB

\(AB=\sqrt{AO^2-OB^2}\)

Hướng dẫn giải

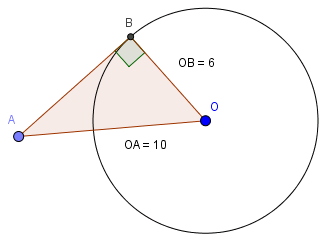
Theo định lí Pytago trong tam giác vuông OAB có:
\(\begin{aligned} & O{{A}^{2}}=O{{B}^{2}}+A{{B}^{2}} \\ & \Rightarrow AB=\sqrt{O{{A}^{2}}-O{{B}^{2}}}=\sqrt{{{10}^{2}}-{{6}^{2}}}=8\,\left( cm \right) \\ \end{aligned}\)

Vậy AB dài \(8cm\).