Giải bài tập SGK Toán 9 Bài: Luyện tập

Trong các biển báo giao thông sau, biển báo nào có tâm đối xứng, biển nào có trục đối xứng?
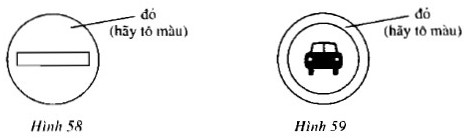
a) Biển cấm đi ngược chiều? (h.58)
b) Biển cấm ô tô (h.59)

Phương pháp giải

Hình có tâm đối xứng O nếu điểm thuộc hình này đối xứng với một điểm cũng thuộc hình này qua O

Hướng dẫn giải

\(-\) Hình 58 có tâm đối xứng là tâm đường tròn, có hai trục đối xứng là hai đường kính vuông góc với các cạnh của hình chữ nhật trong đường tròn.

\(-\) Hình 59 có một trục đối xứng, không có tâm đối xứng.

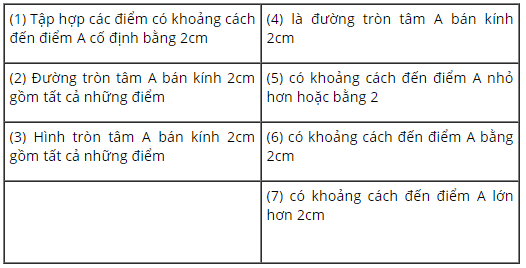
Hãy nối mỗi ô ở cột trái với một ô ở cột phải để được khẳng định đúng:

Phương pháp giải

Định nghĩa đường tròn tâm \(O\) bán kính \(R\) là hình gồm các điểm cách \(O\) một khoảng bằng \(R\). 

Hình tròn tâm \(O\) bán kính \(R\) gồm tất cả các điểm nằm trên đường tròn và nằm trong đường tròn đó.

Hướng dẫn giải

\(-\) Tập hợp các điểm có khoảng cách đến điểm A cố định bằng 2cm là đường tròn tâm A bán kính 2cm.

Nối (1) - (4) 

\(-\) Đường tròn tâm A bán kính 2cm gồm tất cả những điểm có khoảng cách đến điểm A bằng 2cm.

Nối (2) - (6) 

\(-\) Hình tròn tâm A bán kính 2cm gồm tất cả những điểm có khoảng cách đến điểm A nhỏ hơn hoặc bằng 2cm.

Nối (3) - (5) 

Cho góc nhọn xAy và hai điểm B, C thuộc tia Ax. Dựng đường tròn (O) đi qua B và C sao cho tâm O nằm trên tia Ay.

Phương pháp giải

Bước 1. Phân tích:

Giả sử đã dựng được đường tròn \((O)\) thỏa mãn đề bài.

-  Vì \(O\) đi qua \(B,\ C\) nên \(OB=OC\) do đó \(O\) nằm trên đường trung trực \(m\) của \(BC\).

- \(O\) nằm trên tia \(Ay\).

Bước 2. Dựng hình: Dựa vào bước phân tích trên liệt kê thứ tự các phép dựng hình cơ bản.

Bước 3. Chứng minh: Bằng lí luận, chứng minh hình vừa dựng thỏa mãn tất cả các giả thiết của bài toán.

Hướng dẫn giải

- Phân tích

Giả sử đã dựng được đường tròn (O) thỏa mãn đề bài. Tâm O phải thỏa mãn hai điều kiện:

O nằm trên đường trung trực của BC

O nằm trên tia Ay

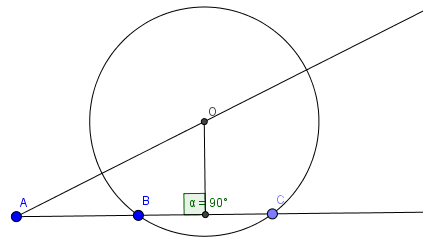
- Dựng hình

+ Dựng góc xAy, trên tia Ax lấy hai điểm B và C.

+ Dựng đường trung trực (d) của BC. (d) cắt tia Ay tại O.

+ Vẽ đường tròn (O, OB). Đường tròn này đi qua B, C. Đó là đường tròn cần dựng.

- Chứng minh:

+ Vì O ∈ đường trung trực (d) của BC nên \(OB = OC\). Suy ra \((O, OB)\) đi qua B, C

+ Vì O ∈ Ay nên (O, OB) thỏa mãn điều kiện đề bài.

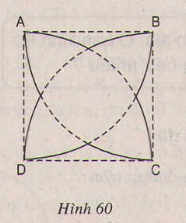
a) Vẽ hình hoa bốn cánh. Hình hoa bốn cánh trên hình 60 được tạo bởi các cung có tâm \(A, B, C, D\) (trong đó \(A, B, C, D\) là các đình của một hình vuông và tâm của cung là tâm của đường tròn chứa cung đó). Hãy vẽ lại hình 60 vào vở.

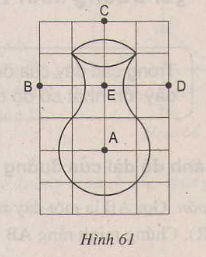
b) Vẽ lọ hoa. Chiếc lọ hoa trên hình 61 được vẽ trên giấy kẻ ô vuông bởi năm cung có tâm \(A, B, C, D, E\). Hãy vẽ lại hình 61 vào giấy kẻ ô vuông.

Phương pháp giải

Sử dụng định lí Pytago để tính độ dài các đường chéo của hình vuông có cạnh là \(1cm\).

Hướng dẫn giải

a) Cách vẽ:

\(-\) Vẽ hình vuông ABCD.

\(-\) Vẽ cung tròn tâm A, bán kính AB (hoặc AD). Cung tròn này đi qua B, D.

\(-\) Tương tự với các cung tròn còn lại.

Ta được bốn cung tròn tạo thành hình hoa bốn cánh.

b) Cách vẽ:

\(-\) Kẻ lại các ô vuông và lấy các điểm như hình 61.

\(-\) Lần lượt vẽ các cung tròn có tâm là các điểm A, B, C, D, E và bán kính là đường chéo của ô vuông.

Ta được năm cung tròn liền nét với nhau tạo thành hình chiếc lọ hoa.