Giải bài tập SGK Toán 9 Bài 7: Vị trí tương đối của hai đường tròn

(7)
140 lượt xem
Share

Dựa theo cấu trúc SGK Toán 9, eLib xin mời các em học sinh tham khảo giải bài tập bài Vị trí tương đối của hai đường tròn trang 119. Với các bài tập có lời giải chi tiết tương ứng với từng bài, hi vọng rằng đây sẽ là tài liệu giúp các em học tập tốt hơn.

Mục lục nội dung

Giải bài tập SGK Toán 9 Bài 7: Vị trí tương đối của hai đường tròn

1. Giải bài 33 trang 119 SGK Toán 9 tập 1

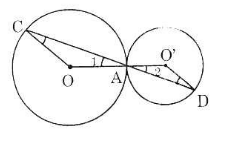
Trên hình 89, hai đường tròn tiếp xúc nhau tại A. Chứng minh rằng OC // O'D.

Phương pháp giải

Chứng minh góc C = D (hai góc ở vị trí so le trong bằng nhau)

Hướng dẫn giải

Ta có: \(OA = OC\) (cùng bằng bán kính (O))

Suy ra \(ΔOAC\) cân tại O.

\(\Rightarrow \widehat{C}=\widehat{OAC}\,\left( 1 \right)\)

Tương tự, \(ΔO'AD\) cân tại O'

\(\Rightarrow \widehat{D}=\widehat{O'AD}\,\left( 2 \right)\)

Mà \(\widehat{OAC}=\widehat{O'AD}\) là hai góc đối đỉnh (3)

Từ (1), (2) và (3) \(\Rightarrow \widehat{C}=\widehat{D} \)

Vậy \(OC // O'D\) (hai góc so le trong bằng nhau).

2. Giải bài 34 trang 119 SGK Toán 9 tập 1

Cho hai đường tròn \((O; 20cm)\) và \((O'; 15cm)\) cắt nhau tại A và B. Tính đoạn nối tâm OO', biết rằng \(AB = 24 cm\). (Xét hai trường hợp: O và O' nằm khác phía đối với AB; O và O' nằm cùng phía đối với AB).

Phương pháp giải

Trường hợp 1: O và O' nằm khác phía đối với AB

Gọi I là giao điểm của OO' và AB

Áp dụng định lí Pytago tính OI, IO' trong tam giác vuông IAO và tam giác IAO’

Vậy OO' = OI + IO'

Trường hợp 2: O và O’ nằm cùng phía với AB

Tương tự trường hợp 1, ta tính dộ dài OI, IO'

Vậy OO’=OI - O’I

Hướng dẫn giải

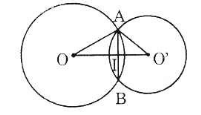
Trường hợp 1: O và O' nằm khác phía đối với AB

Gọi I là giao điểm của OO' và AB. Ta có:

\(AB ⊥ OO'\) và \(AI = IB = 12\)

Áp dụng định lí Pytago trong tam giác vuông IAO, ta có:

\(\begin{aligned} & O{{A}^{2}}=O{{I}^{2}}+I{{A}^{2}} \\ & \Rightarrow OI=\sqrt{O{{A}^{2}}-I{{A}^{2}}}=\sqrt{{{20}^{2}}-{{12}^{2}}}=16\,\left( cm \right) \\ \end{aligned}\)

Áp dung định lí Pytago trong tam giác vuông IAO’, ta có:

\(\begin{aligned} & O'{{A}^{2}}=O'{{I}^{2}}+I{{A}^{2}} \\ & \Rightarrow O'I=\sqrt{O'{{A}^{2}}-I{{A}^{2}}}=\sqrt{{{15}^{2}}-{{12}^{2}}}=9\,\left( cm \right) \\ \end{aligned}\)

Vậy \(OO' = OI + IO' = 16 + 9 = 25\) (cm)

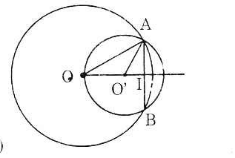
Trường hợp 2: O và O’ nằm cùng phía với AB

Tương tự, ta tính được: \(OI=16cm, O’I=9 cm\)

Suy ra \(OO’=OI-O’I=16-9=7(cm)\)

(7)
140 lượt xem
Share
Ngày:15/10/2020 Chia sẻ bởi:Minh Ngoan
TẢI VỀ XEM ONLINE

CÓ THỂ BẠN QUAN TÂM