Giải bài tập SGK Toán 12 Bài 2: Phương trình mặt phẳng

Viết phương trình mặt phẳng

a) Đi qua điểm M(1; -2; 4) và nhận \(\overrightarrow{n}= (2; 3; 5)\) làm vectơ pháp tuyến

b) Đi qua điểm A(0 ; -1 ; 2) và song song với giá của các vectơ \(\overrightarrow{u}(3; 2; 1)\)và \(\overrightarrow{v}(-3; 0; 1)\)

c) Đi qua ba điểm A(-3 ; 0 ; 0), B(0 ; -2 ; 0) và C(0 ; 0 ; -1)

Phương pháp giải

Mặt phẳng (P) đi qua điểm \({{M_0}({x_0};{y_0};{z_0})}\), nhận vectơ \({\vec n = (A;B;C)}\) làm VTPT có phương trình tổng quát là:

\(A(x-x_0)+B(y-y_0)+C(z-z_0)=0\)

Hướng dẫn giải

Câu a

Măt phẳng \((\alpha )\) đi qua điểm M(1; -2; 4) và nhận = (2; 3; 5) làm vectơ pháp tuyến nên có phương trình:

\((\alpha )\): 2(x - 1) + 3(x +2) + 5(z - 4) = 0 ⇔ 2x + 3y + 5z -16 = 0.

Câu b

\(\left[ {\vec u.\vec v} \right] = \left( {\left| {\begin{array}{*{20}{c}} 2&1\\ 0&1 \end{array}} \right|;\left| {\begin{array}{*{20}{c}} 1&3\\ 1&{ - 3} \end{array}} \right|;\begin{array}{*{20}{c}} 3&2\\ { - 3}&0 \end{array}} \right) = (2; - 6;6)\)

Do mặt phẳng \(\left ( \beta \right )\) cần tìm đi qua A(0;-1;2) và song song với giá của hai vectơ \(\vec u\) và \(\vec v\) nên có một vectơ pháp tuyến \(\overrightarrow n = \frac{1}{2}\left[ {\overrightarrow u ;\overrightarrow v } \right] = \left( {1; - 3;3} \right)\).

Vậy \(\left ( \beta \right )\) có phương trình là:

\(1(x - 0) - 3(y + 1) + 3(z - 2) = 0\) hay \(x - 3y + 3z - 9 = 0.\)

Câu c

Mặt phẳng (P) đi qua A(a;0;0), B(0;b;0), C(0;0;c) (a, b, c khác 0) có phương trình tổng quát là: \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\).

Mặt phẳng \((\alpha )\) có phương trình theo đoạn chắn là:

\(\frac{x}{-3}+\frac{y}{-2}+\frac{z}{-1}=1\) hay \(2x+3y+6z+6=0\).

Viết phương trình mặt phẳng trung trực của đoạn thẳng AB với A(2;3;7) và B(4;1;3)

Phương pháp giải

Mặt phẳng trung trực của đoạn thẳng AB là mặt phẳng đi qua trung điểm và vuông góc với đoạn thẳng AB.

Từ đó, ta suy ra trung điểm I của AB thuộc mặt phẳng trung trực, AB chính là một vectơ pháp tuyến của mặt phẳng đó.

Hướng dẫn giải

Ta có lời giải chi tiết bài 2 như sau

Gọi I là trung điểm của AB, ta có: \(\left\{ \begin{array}{l} {x_I} = \frac{{{x_A} + {x_B}}}{2} = 3\\ {y_I} = \frac{{{y_A} + {y_B}}}{2} = 2\\ {z_I} = \frac{{{z_A} + {z_B}}}{2} = 5 \end{array} \right.\).

Vậy I(3;2;5)

Gọi \((\alpha )\) là mặt phẳng trung trực của đoạn AB, ta có \((\alpha )\) đi qua I và có một vectơ pháp tuyến là:\(\overrightarrow{AB}=(2;-2;-4)\)

Vậy phương trình của mặt phẳng \((\alpha )\) là: \(2(x-3)-2(y-2)-4(z-5)=0\Leftrightarrow x-y-2z+9=0\).

a) Lập phương trình của các mặt phẳng tọa độ (Oxy), (Oyz), (Ozx).

b) Lập phương trình của các mặt phẳng đi qua điểm M(2; 6; -3) và lần lượt song song với các mặt phẳng tọa độ.

Phương pháp giải

Câu a: Các mặt phẳng (Oxy), (Oyz), (Ozx) đều đi qua gốc tọa độ O(0;0;0) và lần lượt vuông góc với các trục Oz, Ox, Oy, từ đó ra suy ra được VTPT của các mặt phẳng này.

Câu b: Cho mặt phẳng (P) song song với mặt phẳng (Q):

​Gọi \(\overrightarrow{n}_P\) là một VTPT của (P), \(\overrightarrow{n}_Q\) là một VTPT của (Q) khi đó: \(\overrightarrow{n}_P=\overrightarrow{n}_Q.\)

Giả sử mặt phẳng (P) có phương trình: \(Ax + By + Cz + D = 0\) thì phương trình mặt phẳng (Q) có dạng:

\(Ax + By + Cz + M = 0\,(M \ne D)\)

Hướng dẫn giải

Câu a

Ta có: \(Oz \bot \left( {Oxy} \right)\) nên mặt phẳng (Oxy) nhận vectơ \(\overrightarrow{k}=(0 ; 0 ; 1)\) làm một vectơ pháp tuyến, mà (Oxy) đi qua gốc toạ độ O(0;0;0) nên có phương trình là z = 0.

Ta có: \(Ox \bot \left( {Oyz} \right)\) nên mặt phẳng (Oyz) nhận vectơ \(\overrightarrow{i}=(1 ; 0 ; 0)\) làm một vectơ pháp tuyến, mà (Oyz) đi qua gốc toạ độ O(0;0;0) nên có phương trình là x = 0.

Ta có: \(Oy \bot \left( {Oxz} \right)\) nên mặt phẳng (Oxz) nhận vectơ \(\overrightarrow{j}=(0 ; 1 ; 0)\) làm một vectơ pháp tuyến, mà (Oxz) đi qua gốc toạ độ O(0;0;0) nên có phương trình là y = 0.

Câu b

Gọi (P) là mặt phẳng đi qua M(2;6;-3) và song song với (Oxy), suy ra phương tình (P) có dạng: z+m=0 (m khác không).

Mặt khác (P) đi qua M(2;6;-3) nên -3+m=0 ⇔ m=3.

Vậy phương trình mặt phẳng (P) là: z+3=0.

Gọi (Q) là mặt phẳng đi qua M(2;6;-3) và song song với (Oyz), suy ra phương tình (Q) có dạng: x+m=0 (m khác không).

Mặt khác (P) đi qua M(2;6;-3) nên 2+m=0 ⇔ m=-2.

Vậy phương trình mặt phẳng (P) là: x-2=0.

Gọi (H) là mặt phẳng đi qua M(2;6;-3) và song song với (Oxz), suy ra phương tình (Q) có dạng: y+m=0 (m khác không).

Mặt khác (P) đi qua M(2;6;-3) nên 6+m=0 ⇔ m=-6.

Vậy phương trình mặt phẳng (P) là: y-6=0.

Lập phương trình mặt phẳng

a) Chứa trục Ox và điểm P(4 ; -1 ; 2)

b) Chứa trục Oy và điểm Q(1 ; 4 ;-3)

c) Chứa trục Oz và điểm R(3 ; -4 ; 7)

Phương pháp giải

Mặt phẳng chứa trục tọa độ và đi qua một điểm nên ra sẽ xác định được cặp VTCP của mặt phẳng đó là một vectơ đơn vị và một vectơ có điểm đầu là góc tọa độ O, điểm cuối là điểm mà mặt phẳng đó đi qua. Từ đó ta xác định được VTPT của mặt phẳng là tích có hướng của cặp VTCP và viết được phương trình mặt phẳng.

Hướng dẫn giải

Câu a

Mặt phẳng \((\alpha )\) chứa \(P(4;-1;2)\) và trục Ox nên \((\alpha )\) có cặp vectơ chỉ phương là \(\vec{i}=(1;0;0)\) và \(\overrightarrow{OP}=(4;-1;2)\).

Do đó \((\alpha )\) có một vectơ pháp tuyến là \(\vec{n}=\left [ \vec{i},\overrightarrow{OP} \right ]=(0;-2;-1)\).

Phương trình của \((\alpha )\) là: 0(x-4) - 2(y+1) - 1(z-2) = 0 hay -2y - z = 0 ⇔ 2y + z = 0.

Câu b

Mặt phẳng \((\beta )\) chứa Q(1;4;-3) và trục Oy thì \((\beta )\) có cặp vectơ chỉ phương là \(\vec{j}=(0;1;0)\) và \(\overrightarrow{OQ}=(1;4;-3)\).

Do đó \((\beta )\) có một vectơ pháp tuyến là \(\vec{n}=\left [ \vec{j},\overline{OQ} \right ]=(-3;0;-1)\).

Phương trình của \((\beta )\) là: -3(x-1) - 0(y-4) - 1(z+3) = 0 hay \(-3x-z=0\Leftrightarrow 3x+z=0\).

Câu c

Mặt phẳng (ɣ) chứa điểm R(3; -4; 7) và trục Oz và (ɣ) có cặp vectơ chỉ phương là \(\vec{k}=(0;0;1)\) và \(\overrightarrow{OR}=(3;-4;7)\).

Do đó (ɣ) có một vectơ pháp tuyến là \(\vec{n}=\left [ \vec{k},\overrightarrow{OR} \right ]=(4;3;0)\).

Phương trình mặt phẳng (ɣ) là: 4(x-3) + 3(x+4) + 0(z-7) = 0 hay 4x + 3y = 0.

Cho tứ diện có các đỉnh là A(5 ; 1 ; 3), B(1 ; 6 ; 2), C(5 ; 0 ; 4), D(4 ; 0 ; 6).

a) Hãy viết các phương trình mặt phẳng (ACD) và (BCD)

b) Hãy viết phương trình mặt phẳng (α) đi qua cạnh AB và song song với cạnh CD.

Phương pháp giải

Mặt phẳng đi qua 3 điểm A, B, C không thẳng hàng có một VTPT \(\vec{n}=\left [ \overrightarrow{AB};\overrightarrow{AC} \right ]\).

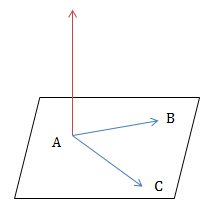
Giả sử mặt phẳng (P), có cặp VTCP là \(\vec u_1\) và \(\vec u_2\) thì \(\vec{n}=\left [ \overrightarrow{u_1}; \overrightarrow{u_2} \right ]\) là một VTPT của mặt phẳng (P).

Hướng dẫn giải

Câu a

Ta có \(\overrightarrow{AC}=(0;-1;1); \overrightarrow{AD}=(-1;-1;3)\)

Mặt phẳng (ACD) có vecto pháp tuyến \(\vec{n}=\left [ \overrightarrow{AC}, \overrightarrow{AD} \right ]= (-2;-1;-1)\)

Vậy phương trình của mặt phẳng (ACD) là:

\(-2(x-5)-1(y-1)-1(z-3)=0\Leftrightarrow 2x+y+z-14=0\)

Câu b

Ta có: \(\overrightarrow{AB}=(-4;5;-1); \overrightarrow{CD}=(-1;0;2)\).

Suy ra mặt phẳng \((\alpha )\) đi qua AB và song song với CD nên có một vectơ pháp tuyến là \(\vec{n}=\left [ \overrightarrow{AB}, \overrightarrow{CD} \right ]=(10;9;5)\).

Vậy phương trình của mặt phẳng \((\alpha )\) là:

\(10(x-5)+9(y-1)+5(z-3)=0\Leftrightarrow 10x+9y+5z-74=0\).

Viết phương trình mặt phẳng \((\alpha )\) đi qua điểm M(2 ; -1 ; 2) và song song với mặt phẳng \((\beta )\) có phương trình: 2x - y + 3z + 4 = 0.

Phương pháp giải

Cho mặt phẳng (P) song song với mặt phẳng (Q):

​Gọi \(\overrightarrow{n}_P\) là một VTPT của (P), \(\overrightarrow{n}_Q\) là một VTPT của (Q) khi đó: \(\overrightarrow{n}_P=\overrightarrow{n}_Q.\)

Suy ra nếu mặt phẳng (P) có phương trình: \(Ax + By + Cz + D = 0\) thì phương trình mặt phẳng (Q) có dạng:

\(Ax + By + Cz + M = 0\,(M \ne D)\)

Hướng dẫn giải

Mặt phẳng \((\alpha )\) song song với mặt phẳng \((\beta )\) nên \((\alpha )\) có dạng: \((\alpha ):2x-y+3z+D=0\) (\(D\ne4\)).

Vì \((\alpha )\) qua M(2;-1;2) nên 2.2 + 1 + 3.2 + D = 0 ⇒ D = -11.

Vậy phương trình mặt phẳng \((\alpha )\) là: 2x - y + 3z - 11 = 0.

Lập phương trình mặt phẳng (\(\alpha\)) đi qua hai điểm A( 1; 0 ; 1), B(5 ; 2 ; 3) và vuông góc với mặt phẳng: 2x - y + z - 7 = 0. 

Phương pháp giải

Nếu mặt phẳng \((\beta )\) vuông góc với mặt phẳng \((\alpha )\) thì VTPT của \((\beta )\) sẽ có phương song song với mặt phẳng \((\alpha )\), hay còn gọi đó là một VTCP của mặt phẳng \((\alpha )\).

Hướng dẫn giải

Lời giải chi tiết bài 7 như sau

Ta có \(\overrightarrow{AB}=(4;2;2)\).

Vectơ pháp tuyến của mp \((\beta )\) có phương trình 2x - y + z - 7 = 0 là \(\vec{n}_{(\beta )}=(2;-1;1)\). Do mp\((\alpha )\) vuông góc với mp \((\beta )\) nên \(\vec{n}_{(\beta )}=(2;-1;1)\) có phương song song với mp\((\alpha )\).

Suy ra: mp\((\alpha )\) có cặp VTCP là \(\overrightarrow{AB}=(4;2;2)\) và \(\vec{n}_{(\beta )}=(2;-1;1)\).

Vậy mp\((\alpha )\) có một vectơ pháp tuyến là \(\vec{n}_{\alpha }=\left [ \overrightarrow{AB}, \vec{n}_{\beta } \right ]= (1;0;-2)\).

Vậy phương trình của mặt phẳng \((\alpha )\) là:

1(x - 1) + 0(y - 0) - 2(z - 1) = 0 ⇔ x - 2z + 1 = 0.

Xác định giá trị của m và n để mỗi cặp mặt phẳng sau đây là một cặp mặt phẳng song song với nhau:

a) \(2x + my + 3z - 5 = 0\) và  \(\small nx - 8y - 6z + 2 = 0\);

b) \(\small 3x - 5y + mz - 3 = 0\)  và  \(\small 2x + ny - 3z + 1 = 0\);

Phương pháp giải

Cho hai mặt phẳng \((\alpha _1) \ A_1x+B_1y+C_1z+D_1=0\) có một VTPT \(\vec{n_1}=(A_1;B_1;C_1)\) và \((\alpha _2) \ A_2x+B_2y+C_2z+D_2=0\) có một VTPT \(\vec{n_2}=(A_2;B_2;C_2)\).

Khi đó vị trí tương đối giữa \((\alpha_1)\) và \((\alpha_2)\) được xác định như sau:

\((\alpha _1)//(\alpha _2)\) khi và chỉ khi \(\left\{\begin{matrix} \vec{n_1}=k.\vec{n_2}\\ D_1\neq D_2 \end{matrix}\right.\).

Nếu \(A_2, B_2, C_2, D_2 \neq 0\): \((\alpha _1)//(\alpha _2)\Leftrightarrow \frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}\neq \frac{D_1}{D_2}\).

Hướng dẫn giải

Câu a

Xét hai mặt phẳng \((\alpha )\): 2x + my + 3z - 5 = 0  và \((\beta )\): nx - 8y - 6z + 2 = 0

Với n=0, ta có \((\alpha )\): 2x + my + 3z - 5 = 0 và  \((\beta )\): - 8y - 6z + 2 = 0. Không tồn tại m để hai mặt phẳng song song với nhau.

Với \(n \ne 0\), \((\alpha ) // (\beta )\) thì:  ⇔ \(\left\{ \begin{array}{l} \frac{2}{n} = \frac{3}{6}\\ \frac{m}{{ - 8}} = \frac{3}{6} \end{array} \right.\)  ⇔ .

Câu b

Xét hai mặt phẳng \((\alpha )\): 3x - 5y + mz - 3 = 0 và \((\beta )\): 2x + ny - 3z + 1 = 0.

Với n=0 ta có  \((\alpha )\): 3x - 5y + mz - 3 = 0 và \((\beta )\): 2x - 3z + 1 = 0. Không tồn tại m để hai mặt phẳng song song với nhau.

Với \(n \ne 0\), \((\alpha ) // (\beta )\) thì:  ⇔ \(\left\{ \begin{array}{l} - \frac{5}{n} = \frac{3}{2}\\ \frac{m}{3} = \frac{3}{2} \end{array} \right.\) ⇔ \(\left\{\begin{matrix} n=-\frac{10}{3} & \\ \\ m=-\frac{9}{2} & \end{matrix}\right.\).

Tính khoảng cách từ điểm A(2 ; 4 ; -3) lần lượt đến các mặt phẳng sau:

a) \(2x - y + 2z - 9 = 0\)

b) \(\small 12x - 5z + 5 = 0\)

c) \(\small x = 0\)

Phương pháp giải

Cho mặt phẳng (P): \(Ax+By+Cz+D=0 \ \ (A^2+B^2+C^2\neq 0)\)
và điểm \(M(x_0,y_0,z_0)\).
Khoảng cách từ M đến (P) được xác định bởi công thức: \(d(M;(P))=\frac{\left | Ax_0+Ay_0+Az_0+D \right |}{\sqrt{A^2+B^2+C^2}}\).

Hướng dẫn giải

Câu a

Với mặt phẳng \((\alpha ): 2x - y + 2z - 9 = 0\)

Ta có: .

Câu b

Với mặt phẳng \((\beta ): \small 12x - 5z + 5 = 0\)

Ta có: \(d(A,(Q))=\frac{|12.2-5.(-3)+5)}{\sqrt{144+25}}=\frac{44}{13}.\)

Câu c

Với mặt phẳng \((\gamma ): x=0\)

Ta có: \(d(A,(\gamma )) = \frac{\left | 2 \right |}{\sqrt{1+0+0}}=2\).

Giải các bài toán sau đây bằng phương pháp tọa độ. Cho hình lập phương ABCD.A'B'C'D' cạnh bằng 1.

a) Chứng minh rằng hai mặt phẳng (AB'D') và (BC'D) song song với nhau.

b) Tính khoảng cách giữa hai mặt phẳng nói trên.

Phương pháp giải

Từ dữ kiện đề bài, ta chọn một đỉnh bất kì của hình lập phương là gốc tọa độ. Khi đó, 3 cạnh của hình lập phương đi qua đỉnh đó chính là phương của các trục Ox, Oy, Oz.

Sau khi xây dựng xong hệ trục tọa độ, ta xác định tọa độ các đỉnh lúc này và tiến hành giải bài toán bằng phương pháp tọa độ trong không gian.

Giải sử, mặt phẳng (P) song song mặt phẳng (Q) thì khoảng cách từ (P) đến (Q) bằng khoảng cách từ một điểm bất kì thuộc (P) đến mặt phẳng (Q).

Hướng dẫn giải

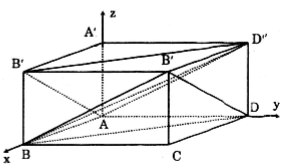
Xây dựng hệ trục tọa độ Oxyz như hình vẽ ta có tọa độ các đỉnh của hình lập phương là:

A(0;0;0), B(1;0;0), D(0;1;0), A'(0;0;1)

A'(0;0;1), B'(1;0;1),  C'(1;1;1), D'(0;1;1)

Câu a

Đặt \((\alpha )=(A'B'D')\) và \((\beta )=(BCD)\)

Ta có: \(\overrightarrow{AB'}=(1;0;1); \overrightarrow{AD'}=(0;1;1)\) 

Suy ra mặt phẳng \((\alpha )\) có vecto pháp tuyến là \(\vec{n}=\left [ \overrightarrow{AB'},\overrightarrow{AD'} \right ]=(1;1;-1)\)

Vậy phương trình của mặt phẳng \((\alpha )\) là \(x+y-z=0\).

Ta có \(\overrightarrow{BC'}=(0;1;1)\)và \(\overrightarrow{BD}=(-1;1;0)\)

Suy ra mặt phẳng \((\beta )\) có vecto pháp tuyến là \(\vec{n}=\left [ \overrightarrow{BC'}, \overrightarrow{BD} \right ]=(-1;-1;1)\)

Phương trình mp \((\beta )\) là: \(-1(x-1) -1.y+1.z=0\Leftrightarrow x+y-z-1=0\).

Ta có

\(\frac{1}{1}=\frac{1}{1}=\frac{-1}{-1}\neq \frac{0}{-1}\), vậy hai mặt phẳng \((\alpha )\) và \((\beta )\) song song nhau.

Câu b

Do mặt phẳng \((\alpha )\) và \((\beta )\) song song nhau nên:

\(d((\alpha ),(\beta ))=d(A,(\beta ))=\frac{\left | -1 \right |}{\sqrt{1^2+1^2+(-1)^2}}= \frac{1}{\sqrt{3}}\)