Giải bài tập SGK Toán 12 Bài 1: Hệ tọa độ trong không gian
Phần hướng dẫn giải bài tập Hệ tọa độ trong không gian sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Hình học 12 Cơ bản và Nâng cao.
Mục lục nội dung

1. Giải bài 1 trang 68 SGK Hình học 12
Cho ba vectơ \(\overrightarrow{a}=(2; -5; 3)\), \(\overrightarrow{b}=(0; 2; -1)\), \(\overrightarrow{c}=(1; 7; 2)\).
a) Tính tọa độ của vectơ \(\overrightarrow{d}=4.\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+3\overrightarrow{c}\).
b) Tính tọa độ của vectơ \(\overrightarrow{e}=\overrightarrow{a}-4\overrightarrow{b}-2\overrightarrow{c}\).
Phương pháp giải
Áp dụng các công thức cộng, trừ hai vectơ, nhân một số với một vectơ.
Cho hai vectơ \(\vec{u}=(x;y;z)\) và \(\vec{u'}=(x';y'; z')\):
\(\vec{u}+\vec{u'}=(x+x';y+y';z+ z')\)
\(\vec{u}-\vec{u'}=(x-x';y-y';z- z')\)
\(k\vec{u}=(kx;ky;kz)\)
Hướng dẫn giải
Câu a
Ta có
\(4\vec{a}=( 8; -20; 12)\); \(\frac{1}{3}\overrightarrow{b}= (0;-\frac{2}{3}; \frac{1}{3})\); \(3\vec{c} = ( 3; 21; 6)\).
Do đó \(\overrightarrow{d}=4\vec{a}-\frac{1}{3}+3\vec{c}= (11; \frac{1}{3};\frac{55}{3})\).
Câu b
\(\vec a = (2; - 5;3),{\rm{ }} - 4\vec b = (0; - 8;4),{\rm{ - 2}}\vec c = ( - 2; - 14; - 4).\)
Do đó: \(\overrightarrow{e}=\vec{a}-4\vec{b}-2\vec{c} =( 0; -27; 3)\)
2. Giải bài 2 trang 68 SGK Hình học 12
Cho ba điểm A = (1; -1; 1), B = (0; 1; 2), C = (1; 0; 1).
Tìm tọa độ trọng tâm G của tam giác ABC.
Phương pháp giải
\(G\) là trọng tâm tam giác \(ABC\) thì: \(\left\{ \begin{array}{l}{x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3}\\{z_G} = \dfrac{{{z_A} + {z_B} + {z_C}}}{3}\end{array} \right.\)
Hướng dẫn giải
\(\left\{ \begin{array}{l}{x_G} = \dfrac{{{x_A} + {x_B} + {x_C}}}{3} = \dfrac{{1 + 0 + 1}}{3} = \dfrac{2}{3}\\{y_G} = \dfrac{{{y_A} + {y_B} + {y_C}}}{3} = \dfrac{{ - 1 + 1 + 0}}{3} = 0\\{z_G} = \dfrac{{{z_A} + {z_B} + {z_C}}}{3} = \dfrac{{1 + 2 + 1}}{3} = \dfrac{4}{3}
\end{array} \right. \Rightarrow G\left( {\dfrac{2}{3};0;\dfrac{4}{3}} \right)\)
3. Giải bài 3 trang 68 SGK Hình học 12
Cho hình hộp \(ABCD.A'B'C'D'\) biết \(A = (1; 0; 1), B = (2; 1; 2), D = (1; -1; 1)\), \(C' (4; 5; -5)\). Tính tọa độ các đỉnh còn lại của hình hộp.
Phương pháp giải
Sử dụng các vector bằng nhau.
Hai vector \(\overrightarrow u \left( {{x_1};{y_1};{z_1}} \right) = \overrightarrow v \left( {{x_2};{y_2};{z_2}} \right) \Leftrightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\\{z_1} = {z_2}\end{array} \right.\)
Hướng dẫn giải
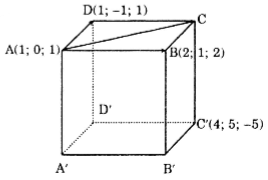
Ta có
\(\overrightarrow{AB}=(1;1;1)\)
\(\overrightarrow{AD}=(0;-1;0)\)
\(\overrightarrow{BC}=\overrightarrow{AD}\Leftrightarrow \left\{\begin{matrix} x_C-2=0\\ y_C-1=-1\\ z_C-2=0 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_C=2\\ y_C=0\\ z_C=2 \end{matrix}\right.\)
Vậy C=(2;0;2)
Suy ra \(\overrightarrow{CC'}=(2;5;-7)\)
Từ \(\overrightarrow{AA'}=\overrightarrow{BB'}= \overrightarrow{DD'}=\overrightarrow{CC'}=(2;5;-7)\)
\(\overrightarrow {AA'} = (2;5; - 7) \Rightarrow\) \(\left\{\begin{matrix} x_{A'}-1=2\\ y_{A'}-0=5\\ z_{A'}-1=-7 \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_{A'}=3\\ y_{A'}=5\\ z_{A'}=-6\\ \end{matrix}\right.\)
Vậy A'(3;5;-6).
\(\overrightarrow {BB'} = (2;5; - 7) \Rightarrow \left\{ {\begin{array}{*{20}{c}} {{x_{B'}} - 2 = 2}\\ {{y_{B'}} - 1 = 5}\\ {{z_{B'}} - 2 = - 7} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{x_{B'}} = 4}\\ {{y_{B'}} = 6}\\ {{z_{B'}} = - 5} \end{array}} \right.\)
Vậy: B'(4;6;-5).
\(\overrightarrow {DD'} = (2;5; - 7) \Rightarrow \left\{ {\begin{array}{*{20}{c}} {{x_{D'}} - 1 = 2}\\ {{y_{D'}} + 1 = 5}\\ {{z_{D'}} - 1 = - 7} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{x_{D'}} = 3}\\ {{y_{D'}} = 4}\\ {{z_{D'}} = - 6} \end{array}} \right.\)
D'=(3;4;-6)
4. Giải bài 4 trang 68 SGK Hình học 12
Tính
a) \(\overrightarrow{a}.\overrightarrow{b}\) với \(\overrightarrow{a}(3; 0; -6),\overrightarrow{b}(2; -4; 0)\).
b) \(\overrightarrow{c}.\overrightarrow{d}\) với \(\overrightarrow{c}(1; -5; 2),\overrightarrow{d}(4; 3; -5)\).
Phương pháp giải
Biểu thức tọa độ của tích vô hướng: \(\left.\begin{matrix} \vec{a}=(x_1;y_1;z_1)\\ \vec{b}=(x_2;y_2;z_2) \end{matrix}\right\} \vec{a}.\vec{b} = x_1.x_2 + y_1.y_2 + z_1.z_2\)
Hướng dẫn giải
Câu a
\(\overrightarrow{a}.\overrightarrow{b} = 3.2 + 0.(-4) +(-6).0 = 6.\)
Câu b
\(\overrightarrow{c}.\overrightarrow{d} = 1.4 + (-5).3 + 2.(-5) = -21.\)
5. Giải bài 5 trang 68 SGK Hình học 12
Tìm tâm và bán kính của các mặt cầu có phương trình sau đây:
a) \(\small x^2 + y^2 + z^2 - 8x - 2y + 1 = 0\).
b) \(\small 3x^2 + 3y^2 + 3z^2 - 6x + 8y + 15z - 3 = 0\).
Phương pháp giải
Cách 1
Phương trình mặt cầu dạng \(x^2+y^2+z^2-2Ax-2By-2Cz+D=0\), điều kiện \(A^2+B^2+C^2-D> 0\).
Khi đó, mặt cầu có tâm \(I(A;B;C)\), bán kính \(R = \sqrt {{A^2} + {B^2} + {C^2} - D} .\)
Cách 2
Đưa phương trình về dạng \((x-a)^2+(y-b)^2+(z-c)^2=R^2\). Khi đó mặt cầu tâm I(a;b;c), bán kính R.
Hướng dẫn giải
Câu a
Cách 1
Xét phương trình: \(\small x^2 + y^2 + z^2 - 8x - 2y + 1 = 0\) có dạng:
\(x^2+y^2+z^2+2Ax+2By+2Cz+D=0\)
Với: \(\left\{ \begin{array}{l} A = 4\\ B = 1\\ C = 0\\ D = 1 \end{array} \right. \Rightarrow {A^2} + {B^2} + {C^2} - D = 16 > 0\)
Suy ra đây là phương trình mặt cầu có tâm I(4; 1; 0) và có bán kính R = 4.
Cách 2
Ta có phương trình : x2 + y2 + z2 – 8x - 2y + 1 = 0
⇔ (x2 - 8x + 16) + (y2 - 2y + 1) +z2 = 16 +1 - 1
⇔ (x – 4)2 + (y – 1)2 + z2 = 42
Đây là mặt cầu tâm I(4; 1; 0) và có bán kính r = 4.
Câu b
Cách 1
Xét phương trình: \(\small 3x^2 + 3y^2 + 3z^2 - 6x + 8y + 15z - 3 = 0 \Leftrightarrow x^2+y^2+z^2-2x+\frac{8}{3}y+5z-1=0\) có dạng:
\(x^2+y^2+z^2+2Ax+2By+2Cz+D=0\)
Với: \(\left\{ \begin{array}{l} A = 1\\ B = - \frac{4}{3}\\ C = - \frac{5}{2}\\ D = - 1 \end{array} \right. \Rightarrow {A^2} + {B^2} + {C^2} - D = \frac{{361}}{{36}} > 0\)
Suy ra đây là phương trình mặt cầu có tâm \(I(1; -\frac{4}{3};-\frac{5}{2})\) và có bán kính là R = .
Cách 2
3x2 + 3y2 + 3z2 – 6x + 8y + 15z – 3 = 0
⇔ x2 + y2 + z2 – 2x + y + 5z – 1 = 0
⇔\((x-1)^{2}+(y+\frac{4}{3})^{2}+(z+\frac{5}{2})^{2} -1-\frac{16}{9}-\frac{25}{4}-1=0\)
⇔ \((x-1)^{2}+(y+\frac{4}{3})^{2}+(z+\frac{5}{2})^{2}= \frac{361}{36}=\frac{19^2}{6^2}\).
Đây là mặt cầu tâm \(I(1; -\frac{4}{3};-\frac{5}{2})\) và có bán kính là R = .
6. Giải bài 6 trang 68 SGK Hình học 12
Lập phương trình mặt cầu trong hai trường hợp sau đây:
a) Có đường kính AB với A(4 ; -3 ; 7), B(2 ; 1 ; 3)
b) Đi qua điểm A = (5; -2; 1) và có tâm C(3; -3; 1)
Phương pháp giải
Từ dữ kiện đề bài, xác định tâm và bán kính mặt cầu để có thể viết được phương trình.
Trong không gian Oxyz, mặt cầu tâm I(a;b;c), bán kính R có phương trình: \((x-a)^2+(y-b)^2+(z-c)^2=R^2.\)
Hướng dẫn giải
Câu a
Tâm I của mặt cầu đường kính AB là trung điểm I của đoạn thảng AB, ta có \(I\left ( \frac{4+2}{2}; \frac{-3+1}{2}; \frac{7+3}{2} \right ) =(3;-1;5)\)
Bán kính mặt cầu: \(R=IA=\sqrt{1^2+(-2)^2+2^2}=3\)
Vậy phương trình mặt cầu đường kính AB là: (x - 3)2 + (y +1)2 + (z – 5)2 = 9.
Câu b
Bán kính \(R = CA = \sqrt{4+1+0}=\sqrt{5}\)
Phương trình mặt cầu là: (x - 3)2 + (y + 3)2 + (z – 1)2 = 5.
Tham khảo thêm
- doc Giải bài tập SGK Toán 12 Bài 2: Phương trình mặt phẳng
- doc Giải bài tập SGK Toán 12 Bài 3: Phương trình đường thẳng trong không gian
- doc Giải bài tập SGK Toán 12 Ôn tập chương 3: Phương pháp toạ độ trong không gian



