Giải bài tập SGK Toán 12 Ôn tập chương 3: Phương pháp toạ độ trong không gian

Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(-2; 1; -1)

a) Chứng minh A, B, C, D là bốn đỉnh của một tứ diện.

b) Tìm góc giữa hai đường thẳng AB và CD

c) Tính độ dài đường cao của hình chóp A.BCD

Phương pháp giải

Câu a: 4 điểm A, B, C, D không đồng phẳng khi và chỉ khi \(\left [ \overrightarrow{AB},\overrightarrow{AC} \right ].\overrightarrow{AD}\neq 0\).

Câu b: \(\cos \left( {AB,CD} \right) = \left| {\cos \left( {\overrightarrow {AB} ,\overrightarrow {CD} } \right)} \right|.\)

Câu c: Viết phương trình mặt phẳng (BCD). Độ dài đường cao của hình chóp A.BCD chính là khoảng cách từ A đến mặt phẳng (BCD).

Hướng dẫn giải

Câu a

Ta có: \(\overrightarrow {AB} = ( - 1;1;0),\,\,\overrightarrow {AC} = ( - 1;0;1),\,\,\overrightarrow {AD} = \left( { - 3;1; - 1} \right)\)

\(\left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right] = \left( {\left| {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right|;\left| {\begin{array}{*{20}{c}} 0&{ - 1}\\ 1&{ - 1} \end{array}} \right|;\left| {\begin{array}{*{20}{c}} { - 1}&1\\ { - 1}&0 \end{array}} \right|} \right) = \left( {1;1;1} \right)\)

\(\left[ {\overrightarrow {AB} ;\overrightarrow {AC} } \right].\overrightarrow {AD} = 1.( - 3) + 1.1 + 1.( - 1) = - 3 \ne 0.\)

Suy ra \(\overrightarrow {AB} ;\overrightarrow {AC} ;\overrightarrow {AD}\) không đồng phẳng hay A, B, C, D là bốn đỉnh một tứ diện.

Câu b

Ta có: \(\overrightarrow{AB}=(-1;1;0); \overrightarrow{CD}=(-2;1;-2)\)

\(cos(AB,CD) = \frac{{\left| {\overrightarrow {AB} .\overrightarrow {CD} } \right|}}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {CD} } \right|}} = \frac{{\left| {2 + 1 + 0} \right|}}{{\sqrt 2 .\sqrt 9 }} = \frac{1}{{\sqrt 2 }}\)

Vậy góc giữa hai đường thẳng AB và CD là 450.

Câu c

Ta có

\(\begin{array}{l} \overrightarrow {BC} = (0; - 1;1),\,\overrightarrow {BD} = \left( { - 2;0; - 1} \right)\\ \Rightarrow \left[ {\overrightarrow {BC} ;\overrightarrow {BD} } \right] = \left( {\left| {\begin{array}{*{20}{c}} { - 1}&1\\ 0&{ - 1} \end{array}} \right|;\left| {\begin{array}{*{20}{c}} 1&0\\ { - 1}&{ - 2} \end{array}} \right|;\left| {\begin{array}{*{20}{c}} 0&{ - 1}\\ { - 2}&0 \end{array}} \right|} \right) = \left( {1; - 2; - 2} \right). \end{array}\)

Mặt phẳng (BCD) đi qua B(0;1;0) nhận \(\overrightarrow n = \left[ {\overrightarrow {BC} ;\overrightarrow {BD} } \right]\) làm VTPT nên có phương trình là: \(1(x - 0) - 2(y - 1) - 2(z - 0) = 0\) hay \(x - 2y - 2z + 2 = 0.\)

Độ dài đường cao của hình chóp A.BCD là khoảng cách từ A đến mp(BCD), ta có:

\(AH=d(A,(BCD))=\frac{\left | 1+2 \right |}{\sqrt{1+4+4}}=1\).

Cho mặt cầu (S) có đường kính là AB biết rằng A(6; 2; -5), B(-4; 0; 7)

a) Tìm tọa độ tâm I và bán kính r của mặt cầu (S).

b) Lập phương trình của mặt cầu (S).

c) Lập phương trình của mặt phẳng (\(\alpha\)) tiếp xúc với mặt cầu (S) tại điểm A.

Phương pháp giải

Câu a: Tâm I của mặt cầu (S) có đường kính AB là trung điểm của AB.

Câu b: Trong không gian Oxyz, mặt cầu tâm I(a;b;c), bán kính R có phương trình: \((x-a)^2+(y-b)^2+(z-c)^2=R^2.\)

Mặt phẳng (\(\alpha\)) tiếp xúc với mặt cầu (S) có tâm I tại điểm A suy ra \(IA \bot \left ( \alpha \right )\). Nên \(\overrightarrow{IA}\) là một VTPT của \(\left ( \alpha \right )\).

Hướng dẫn giải

Câu a

Tâm I của mặt cầu (S) có đường kính AB là trung điểm của AB.

Tọa độ điểm I là: \(\left\{ \begin{array}{l} {x_I} = \frac{{{x_A} + {x_B}}}{2}\\ {y_I} = \frac{{{y_A} + {y_B}}}{2}\\ {z_I} = \frac{{{z_A} + {z_B}}}{2} \end{array} \right. \Rightarrow \left\{ \begin{array}{l} {x_I} = 1\\ {y_I} = 1\\ {z_I} = 1 \end{array} \right.\)

Ta có I(1;1;1), bán kính \(r=IA=\sqrt{62}\).

Câu b

Phương trình của mặt cầu (S) có tâm I(1;1;1), bán kính \(r=\sqrt{62}\) là:

\((x-1)^2+(y-1)^2+(z-1)^2=62\)

Câu c

Mặt phẳng (\(\alpha\)​) tiếp xúc với mặt cầu (S) tại A, suy ra (\(\alpha\)​) có vectơ pháp tuyến là \(\overrightarrow{IA}=(5;1;-6)\)

Vậy phương trình của mặt phẳng (\(\alpha\)​) là:

\(5(x-6)+(y-2)-6(z+5)=0\Leftrightarrow 5x+y-6z-62=0\)

Cho bốn điểm A(-2; 6; 3), B(1; 0; 6), C(0; 2; -1), D(1; 4; 0)

a) Viết phương trình mặt phẳng (BCD). Suy ra ABCD là một tứ diện.

b) Tính chiều cao AH của tứ diện ABCD.

c) Viết phương trình mặt phẳng (\(\alpha\)) chứa AB và song song với CD

Phương pháp giải

Câu a: Mặt phẳng (BCD) có cặp VTCP là \(\overrightarrow {BC} ;\overrightarrow {BD}\) nên có một VTPT là \(\vec{n}=\left [ \overrightarrow{BC};\overrightarrow{BD} \right ].\) Viết phương trình mặt phẳng (BCD), thay tọa độ điểm A vào phương trình (BCD) để kiểm tra 4 điểm ABCD có tạo thành một tứ diện hay không.

Câu b: Chiều cao AH của tứ diện ABCD chính là khoảng cách từ điểm A đến mặt phẳng (BCD).

Câu c: Mp(\(\alpha\)​) chứa AB và song song với CD nên có cặp VCTP là \(\overrightarrow {AB} ;\overrightarrow {CD} .\)

Hướng dẫn giải

Câu a

Ta có: \(\overrightarrow{BC}=(-1;2;-7), \overrightarrow{BD}=(0;4;-6)\)

Mp(BCD) có vecto pháp tuyến: \(\vec{n}=\left [ \overrightarrow{BC};\overrightarrow{BD} \right ]= (16;-6;-4)\)

Mp(BCD) đi qua B(1;0;6) và có vecto pháp tuyến \(\vec{n} =(16;-6;-4)\) nên có phương trình là:

\(16(x-1)-6y-4(z-6)=0\Leftrightarrow 8x-3y-2z+4=0\)

Do \(8.( - 2) - 3.6 - 2.3 + 4 = - 36 \ne 0\)

Nên \(A \notin (BCD)\) suy ra ABCD là một tứ diện.

Câu b

Chiều cao AH của tứ diện là khoảng cách từ A đến mp(BCD)

Ta có: \(AH=d(A,BCD)=\frac{\left | 8(-2)-3.6-2.3+4 \right |}{\sqrt{8^2+(-3)^2+(-2)^2}}= \frac{36}{\sqrt{77}}\)

Câu c

Ta có: \(\overrightarrow{AB}=(3;-6;3), \overrightarrow{CD}=(1;2;1)\)

Mp(\(\alpha\)​) chứa AB và song song với CD nên có cặp VCTP là \(\overrightarrow {AB} ;\overrightarrow {CD} .\)

Suy ra (\(\alpha\)​) có một vectơ pháp tuyến \(\vec{n}=\left [ \overrightarrow{AB};\overrightarrow{CD} \right ]=(-12;0;12)\).

Mặt khác (\(\alpha\)​) chứ AB nên đi qua B(1;0;6).

Nên phương trình mặt phẳng (\(\alpha\)​) là:

\(-12(x-1)+0(y-0)+12(z-6)=0\Leftrightarrow x-z+5=0\).

Lập phương trình tham số của đường thẳng:

a) Đi qua hai điểm A(1;0;-3), B(2;-1;0)

b) Đi qua điểm M(2;3;-5) và song song với đường thẳng \(\Delta\) có phương trình: \(\left\{\begin{matrix} x=-2+2t\\ y=3-4t\\ z=-5t \end{matrix}\right.\)

Phương pháp giải

Câu a: Đường thẳng AB có \(\overrightarrow {AB}\)  là một vectơ chỉ phương.

Câu b: \(\Delta\) có VTCP \(\vec a\), d song song với \(\Delta\) thì d cũng nhận \(\vec a\) làm một VTCP.

Hướng dẫn giải

Câu a

Ta có: \(\overrightarrow {AB} = (2; - 1;3)\)

Đường thẳng AB đi qua A(1;0;-3) có vectơ chỉ phương \(\overrightarrow {AB} = (2; - 1;3)\) nên có phương trình tham số là: \(\left\{\begin{matrix} x=1+2t\\ y=-t\\ z=-3+3t \end{matrix}\right.\)

Câu b

Đường thẳng \(\Delta\) có vecto chỉ phương là: \(\overrightarrow a = \left( {2; - 4; - 5} \right)\)

Đường thẳng d đi qua M(2;3;-5) song song với \(\Delta\) nên nhận \(\overrightarrow a = \left( {2; - 4; - 5} \right)\) làm vectơ chỉ phương.

Vậy phương trình tham số của d là: \(\left\{\begin{matrix} x=2+2t\\ y=3-4t\\ z=-5-5t \end{matrix}\right.\)

Cho mặt cầu (S) có phương trình (x – 3)2 + (y + 2)2 + (z – 1)2 = 100 và mặt phẳng \((\alpha )\) có phương trình 2x – 2y – z + 9 = 0. Mp \((\alpha )\) cắt mặt cầu (S) theo một đường tròn (C). Hãy xác định tọa độ tâm và tính bán kính của đường tròn (C).

Phương pháp giải

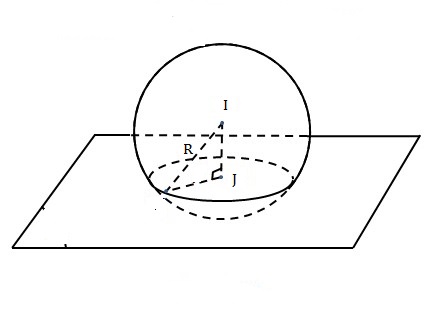
Trước khi giải bài 5, ta ôn lại vị trí tương đối giữa mặt phẳng và mặt cầu đã học ở chương 2 Hình học 12:

Cho mặt cầu S(O;r) tâm O bán kính r và mặt phẳng (P); H là hình chiếu vuông góc của O lên mặt phẳng (P).

Khi đó h=OH là khoảng cách từ O đến mặt phẳng (P). 

• Nếu h=r thì (P) tiếp xúc mặt cầu.

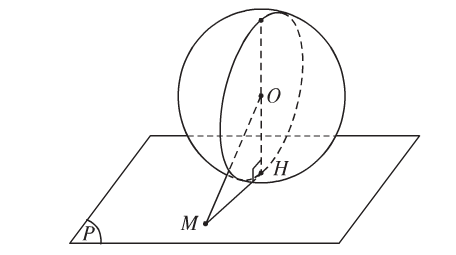
Ghi nhớ: Điều kiện cần và đủ để mặt phẳng (P) tiếp xúc với mặt cầu S(O;r) tại điểm H là (P) vuông góc với bán kính OH tại điểm H đó.

• Nếu h>r thì (P) không có điểm chung với mặt cầu.

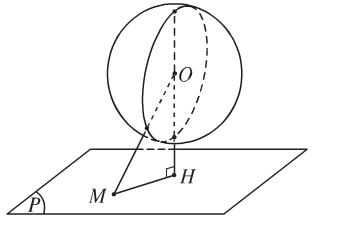
• Nếu h < r thì (P) cắt mặt cầu S(O;r) theo giao tuyến là một đường tròn tâm H bán kính \(r' = \sqrt {{r^2} - {h^2}} .\)

​

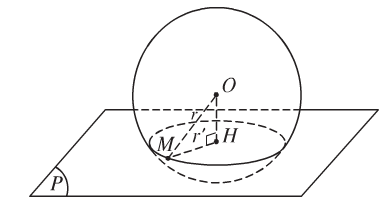
Hướng dẫn giải

Mặt cầu (S) có tâm là I(3;-2;1) và có bán kính R = 10.

\(d(I,(\alpha ))=\frac{\left | 2.3+2.2-1+9 \right |}{\sqrt{2^2+2^2+1^2}}=6\)

Ta có: \(d(I,(\alpha ))=6< 10\), suy ra mặt phẳng \((\alpha )\) cắt (S) theo một đường tròn (C) chính là hình chiếu vuông góc của I trên mặt phẳng \((\alpha )\).

Mặt phẳng \((\alpha )\) có VTPT \(\overrightarrow n = \left( {2; - 2; - 1} \right)\).

Gọi \(\Delta\) là đường thẳng đi qua I(3;-2;1) và vuông góc với \((\alpha )\) suy ra \(\Delta\) nhận \(\overrightarrow n = \left( {2; - 2; - 1} \right)\) làm VTCP:

Vậy phương trình tham số của \(\Delta\) là: \(\left\{\begin{matrix} x=3+2t\\ y=-2-2t\\ z=1-t \end{matrix}\right.\)

\(\Delta\) cắt \((\alpha )\) tại J(3+2t; -2-2t; 1-t). Vì \(J\in (\alpha )\) nên ta có:

\(2(3+2t) -2(-2-2t) - (1-t)+9=0\Leftrightarrow 9t+18=0\Leftrightarrow t=-2\)

Vậy ta được J(-1; 2; 3)

Bán kính r của (C) được tính theo công thức:

\(r=\sqrt{R^2-d^2(I,(\alpha ))}=\sqrt{100-36}=8\)

Vậy đường tròn (C) có tâm J(-1; 2; 3) và bán kính r = 8.

Cho mặt phẳng \((\alpha )\) có phương trình 3x + 5y - z - 2 = 0 và đường thẳng d có phương trình: \(\left\{\begin{matrix} x=12+4t\\ y=9+3t\\ z=1+t \end{matrix}\right.\)

a) Tìm giao điểm M của đường thẳng d và mặt phẳng \((\alpha )\).

b) Viết phương trình mặt phẳng \((\beta )\) chứa điểm M và vuông góc với đường thẳng d.

Phương pháp giải

Câu a: Từ phương trình của đường thẳng d, thay các giá trị của x, y, z theo tham số t vào phương trình \((\alpha )\), giải phương trình tìm t, thay giá trị của t vào phương trình của d suy ra tọa độ giao điểm.

Câu b: Mặt phẳng \((\beta )\) vuông góc với đường thẳng d sẽ nhận VTCP của d làm một VTPT.

Hướng dẫn giải

Câu a

Thay x = 12 + 4t, y = 9 + 3t, z = 1 + t vào phương trình mp \((\alpha )\) ta được:

\(3(12+4t)+5(9+3t)-(1+t)-2=0\Leftrightarrow 26t+78=0\Leftrightarrow t=-3\)

Khi đó x = y = 0, z = -2.

Vậy d cắt \((\alpha )\) tại điểm M(0;0;-2).

Câu b

Đường thẳng d có vecto chỉ phương là \(\vec{a_d}=(4;3;1)\)

Mp \((\beta )\) vuông góc với d thì \((\alpha )\) nhận \(\vec{n}=\vec{a_d}=(4;3;1)\) làm một vectơ pháp tuyến.

Mặc khác \((\beta )\) chưa M(0;0;-2) nên \((\beta )\) có phương trình là:

\(4(x-0)+3(y-0)+1(z+2)=0\Leftrightarrow 4x+3y+z+2=0\).

Cho điểm A(-1;2;-3), vecto \(\vec{a}=(6;-2;-3)\) và đường thẳng d có phương trình: \(\left\{\begin{matrix} x=1+3t\\ y=-1+2t\\ z=3-5t \end{matrix}\right.\)

a) Viết phương trình mặt phẳng (\(\alpha\)) chứa điểm A và vuông góc với \(\vec a.\)

b) Tìm giao điểm của d và (\(\alpha\)).

c) Viết phương trình đường thẳng \(\Delta\) đi qua điểm A, vuông góc với \(\vec{a}\) và cắt đường thẳng d.

Phương pháp giải

Viết phương trình đường thẳng \(\Delta\) đi qua điểm A, vuông góc với đường thẳng d1 hoặc song song với mặt phẳng (P) (trong bài 7 dữ kiện được thay đổi thành vuông góc với \(\vec{a}\)) và cắt đường thẳng d2, cho trước.

Hướng dẫn giải

Câu a

Mặt phẳng (\(\alpha\)) đi qua A(-1;2;-3) có vecto pháp tuyến \(\vec{n}=\vec{a}=(6;-2;-3)=0\) nên có phương trình là:

\(6(x+1)-2(y-2)-3(z+3)=0\Leftrightarrow 6x-2y+3z+1=0\) (1)

Câu b

Thay x = 1 + 3t, y = -1 + 2t, z = 3 - 5t vào phương trình (1) ta được:

\(6(1+3t)-2(-1+2t)-3(3-5t)+1=0\Leftrightarrow t=0\)

Khi đó: \(x=1,y=-1,z=3\).

Vậy d cắt (\(\alpha\)) tại điểm M(1;-1;3).

Câu c

Đường thẳng \(\Delta\) đi qua A vuông góc với giá \(\vec{a}\) và cắt đường thẳng d chính là đường thẳng AM.

\(\Delta\) có vecto chỉ phương là \(\overrightarrow{AM}=(2;-3;6)\)

Phương trình tham số của \(\Delta\) là: \(\left\{\begin{matrix} x=1+2t\\ y=-1-3t\\ z=3+6t \end{matrix}\right.\)

Viết phương trình mặt phẳng \((\alpha )\) tiếp xúc với mặt cầu

\((S): x^2+y^2+z^2-10x+2y+26z+170=0\)

và song song với hai đường thẳng \(d:\left\{\begin{matrix} x=-5+2t\\ y=1-3t\\ z=-13+2t \end{matrix}\right.;d':\left\{\begin{matrix} x=-7+3t\\ y=-1-2t\\ z=8 \end{matrix}\right.\)

Phương pháp giải

Mặt phẳng \(\left ( \alpha \right )\) song song với d và d' nên sẽ có cặp VTCP là \(\vec a;\vec a'\) là các VTCP của d và d'. Từ đó ta suy ra được VTPT của \(\left ( \alpha \right )\).

Qua đó ta sẽ viết được dạng của phương trình tổng quát mặt phẳng \(\left ( \alpha \right )\): \(Ax+By+Cz+D=0\) với A, B, C đã biết.

Dựa vào dữ kiện \(\left ( \alpha \right )\) tiếp xúc với (S) ta sẽ tìm được D.

Hướng dẫn giải

Lời giải chi tiết bài 8 như sau

Đường thẳng d và d' lần lượt có vecto chỉ là \(\vec{a}=(2;-3;2)\) và \(\vec{a'}=(3;-2;0)\)

Mặt phẳng \((\alpha )\) song song với d và d' có vecto pháp tuyến

\(\vec{n}=\left [ \vec{a}, \vec{a'} \right ]=(4;6;5)\)

Vậy \((\alpha )\) có dạng: \(4x+6y+5z+D=0\)

Mặt cầu (S) có tâm I(5; -1; -13) và bán kính \(R=\sqrt{a^2+b^2+c^2-d}=\sqrt{25+1+169-170}=5\)

Ta có: \((\alpha )\) tiếp xúc với (S) \(\Leftrightarrow d(I,(\alpha ))=R\)

\(\Leftrightarrow \frac{\left | 4.(-5)+6(-1)+5.(-13)+D \right |}{\sqrt{16+36+25}}= 5\)

\(\Leftrightarrow \left | D-51 \right |=5\sqrt{77}\Leftrightarrow D=51\pm 5\sqrt{77}\)

Vậy ta có hai mặt phẳng \((\alpha )\) thoả mãn đề bài.

Phương trình tổng quát của \((\alpha )\) là:

\(4x+6y+5z+51\pm 5\sqrt{77}=0\).

Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M(1; -1; 2) trên mặt phẳng \((\alpha )\): 2x – y + 2z + 11 = 0

Phương pháp giải

Để tìm hinh chiếu của M lên mặt phẳng \((\alpha )\) ta thực hiện các bước sau:

Bước 1: Viết phương trình đường thẳng d đi qua M và vuông góc \((\alpha )\).

Bước 2: Tìm giao điểm của d và \((\alpha )\).

Bước 3: Giao điểm vừa tìm được chính là hình chiếu vuông góc của điểm M lên mặt phẳng \((\alpha )\).

Hướng dẫn giải

Ta có lời giải chi tiết bài 9 như sau

Gọi d là đường thẳng đi qua M và vuông góc với d thì vecto chỉ phương của d là \(\vec{a_d}=\vec{n_\alpha }=(2;-1;2)\)

Phương trình tham số của đường thẳng d là: \(\left\{\begin{matrix} x=1+2t\\ y=-1-t\\ z=2+2t \end{matrix}\right.\)

Giao điểm H của d và \((\alpha )\) là hình chiếu vuông góc của M trên mp\((\alpha )\).

Thay x = 1 + 2t, y = -1 - t, z = 2 + 2t vào phương trình mp\((\alpha )\), ta được

\(2(1+2t)-(-1-t)+2(2+2t)+11=0\Leftrightarrow 9t+18=0\Leftrightarrow t=-2\)

Khi đó x = -3; y = 1; z = -2.

Vậy H(-3; 1; -2).

Cho điểm M(2; 1; 0) và mặt phẳng \((\alpha )\): x + 3y – z – 27 = 0. Tìm tọa độ điểm M' đối xứng với M qua \((\alpha )\).

Phương pháp giải

Để tìm tọa độ H là hình chiếu vuông góc của điểm M trên mặt phẳng \(\small (\alpha )\), ta thực hiện các bước sau

• Viết phương trình đường thẳng \(\Delta\) đi qua H và vuông góc với \(\small (\alpha )\).
• Tìm tọa độ giao điểm của \(\Delta\) và \(\small (\alpha )\) chính là tọa độ điểm H cần tìm.

Điểm M' đối xứng với M qua \(\small (\alpha )\), suy ra H chính là trung điểm của MM'.

Hướng dẫn giải

Lời giải chi tiết bài 10 như sau

Gọi H là hình chiếu của M lên mp\((\alpha )\).

Gọi d là đường thẳng đi qua M và vuông góc với \((\alpha )\), d có vecto chỉ phương là \(\vec{a_d}=\vec{n_\alpha }=(1;3;-1)\)

Phương trình tham số của d là: \(\left\{\begin{matrix} x=2+t\\ y=1+3t\\ z=-t \end{matrix}\right.\)

Thay x = 2 + t, y = 1+ 3t, z = -t vào phương trình mp \((\alpha )\), ta được:

\((2+t)+3(1+3t)-(-t)-27=0\Leftrightarrow 11t-22=0\Leftrightarrow t=2\)

Khi đó x = 4; y = 7; z = -2.

Vậy H(4; 7; -2)

Vì M' đối xứng với M qua \((\alpha )\) nên:

\(\overrightarrow{MM'}=2\overrightarrow{MH}\Leftrightarrow \left\{\begin{matrix} x_M-2=2(4-2)\\ y_M-1=2(7-1)\\ z_M=2(-2) \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_M=6\\ y_M=13\\ z_M=-4 \end{matrix}\right.\)

Vậy điểm đối xứng của điểm M qua mặt phẳng \((\alpha )\) là M'(6; 13; -4).

Viết phương trình đường thẳng \(\Delta\) vuông góc với mặt phẳng toạ độ (Oxz) và cắt hai đường thẳng: \(d:\left\{\begin{matrix} x=t\\ y=-4+t\\ z=3-t \end{matrix}\right.; d':\left\{\begin{matrix} x=1-2t\\ y=-3+t\\ z=4-5t \end{matrix}\right.\)​

Phương pháp giải

• \(\Delta\) vuông góc với mặt phẳng toạ độ (Oxz) nên sẽ nhận VTPT của mặt phẳng (Oxz) làm VTCP. Như vậy ta chỉ cần tìm một điểm thuộc \(\Delta\) thì ta sẽ viết được phương trình.
• Giả sử M và M' và giao điểm của \(\Delta\) với d và d' thì \(\overrightarrow {MM'}\) sẽ cùng phương với VTCP của \(\Delta\).

Hướng dẫn giải

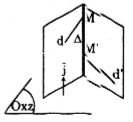
\(\Delta\) vuông góc với mặt phẳng tạo độ (Oxz) nên \(\Delta\) có vecto chỉ phương là \(\vec{j}=(0;1;0)\)

Gọi M(t;-4+t; 3 -t) và M'(1-2t'; -3+t'; 4 - 5t') lần lượt là giao điểm của \(\Delta\) của d và d' (h.34) ta có: \(\overrightarrow{MM'}=k.\vec{j}\)

Suy ra: \(\left\{\begin{matrix} 1-2t'-t=0 \ \ (1)\\ 1+t'-t=k \ \ (2)\\ 1-5t'+t=0 \ \ (3) \end{matrix}\right.\)

Từ (1) và (3) suy ra: \(\left\{\begin{matrix} t=\frac{3}{7}\\ \\ t'=\frac{2}{7} \end{matrix}\right.\)

Thay \(t=\frac{3}{7}\) vào toạ độ M ta được \(M(\frac{3}{7}; -\frac{25}{7};\frac{18}{7})\)

Vậy phương trình tham số của đường thẳng \(\Delta\) là: \(\left\{\begin{matrix} x=\frac{3}{7}\\ \\ y=-\frac{25}{7}+t\\ \\ z=\frac{18}{7} \end{matrix}\right.\)

Tìm tọa độ điểm A' đối xứng với điểm A(1; -2; -5) qua đường thẳng có phương trình:

\(\left\{\begin{matrix} x=1+2t\\ y=-1-t\\ z=2t \end{matrix}\right.\)

Phương pháp giải

Để tìm điểm A' đối xứng với A qua đường thẳng \(\Delta\) ta thực hiện các bước sau:

Tìm tọa độ hình chiếu vuông góc của A lên \(\Delta\)

• Viết phương trình mặt phẳng \(\left ( \alpha \right )\) đi qua A và vuông góc với \(\Delta\).
• Tìm giao điểm H của \(\left ( \alpha \right )\) và \(\Delta\).

Điểm H vừa tìm được chính là trung điểm của A và A'.

Hướng dẫn giải

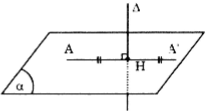
Đường thẳng \(\Delta\) có vecto chỉ phương \(\vec{a}=(2;-1;2)\)

Gọi \((\alpha )\) là mặt phẳng qua A và vuông góc với \(\Delta\) thì \((\alpha )\) có vecto pháp tuyến \(\vec{n}=\vec{a}=(2;-1;2)\) do đó phương trình mp\((\alpha )\) là:

\(2(x-1)-(y+2)+2(z+5)=0\)

\(\Leftrightarrow 2x-y+2z+6=0\)  (1)

Hình chiếu H của A lên \(\Delta\) là giao điểm của \(\Delta\) và \((\alpha )\).

Thay x = 1 + 2t, y = -1 - t, z = 2t vào (1) ta được:

\(2(1+2t)-(-1-t)+4t+6=0\Leftrightarrow 9t+9=0\Leftrightarrow t=-1\)

Khi đó x = -1, y = 0; z = -2

Vậy H(-1; 0; -2)

Vì A' là điểm đối xứng của A qua \(\Delta\) nên:

\(\overrightarrow {AA'} = 2\overrightarrow {AH} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{x_{A'}} - 1 = 2( - 1 - 1)}\\ {{y_{A'}} + 2 = 2(0 + 2)}\\ {{z_{A'}} + 5 = 2.( - 2 + 5)} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{x_{A'}} = - 3}\\ {{y_{A'}} = 2}\\ {{z_{A'}} = 1} \end{array}} \right.\)

Vậy điểm đối xứng với A qua đường thẳng \(\Delta\) là A'(-3; 2; 1)

Trong không gian với hệ tọa độ Oxyz, cho ba vectơ \(\overrightarrow a = ( - 1;1;0);\overrightarrow b = \left( {1;1;0} \right);\overrightarrow c = \left( {1;1;1} \right).\)​

Trong các mệnh đề sau, mệnh đề nào sai?

(A) \(\left | \vec{a} \right |=\sqrt{2}\)

(B) \(\left | \vec{c} \right |=\sqrt{3}\)

(C) \(\vec{a}\perp \vec{b}\)

(D) \(\vec{b}\perp \vec{c}\)

Hướng dẫn giải

\(\vec{b}. \vec{c}=1+1+0=2\neq 0\)

⇒ \(\vec{b}\) không vuông góc với \(\vec{c}\)

⇒ Chọn đáp án D.

Trong không gian với hệ tọa độ Oxyz, cho ba vectơ \(\overrightarrow a = ( - 1;1;0);\overrightarrow b = \left( {1;1;0} \right);\overrightarrow c = \left( {1;1;1} \right).\)​

Trong các mệnh đề sau, mệnh đề nào đúng?

(A) \(\vec{a}.\vec{c}=1\)

(B) \(\vec{a},\vec{b}\) cùng phương

(C) \(cos(\vec{b},\vec{c})=\frac{2}{\sqrt{6}}\)

(D) \(\vec{a}+\vec{b}+\vec{c}=\vec{0}\)

Hướng dẫn giải

\(cos(\vec{b},\vec{c})= \frac{\vec{b}.\vec{c}}{\left |\vec{b} \right |.\left |\vec{c} \right |}= \frac{2}{\sqrt{2}.\sqrt{3}}=\frac{2}{\sqrt{6}}\)

⇒ Chọn đáp án C.

Trong không gian với hệ tọa độ Oxyz, cho ba vectơ \(\overrightarrow a = ( - 1;1;0);\overrightarrow b = \left( {1;1;0} \right);\overrightarrow c = \left( {1;1;1} \right).\)

Cho hình bình hành OADB có \(\overrightarrow{OA}=\overrightarrow{a}, \overrightarrow{OB} =\overrightarrow{b}\) (O là gốc toạ độ). Toạ độ của tâm hình bình hành OADB là: 

(A) (0; 1; 0)

(B) (1; 0; 0)

(C) (1; 0; 1)

(D) (1; 1; 0)

Hướng dẫn giải

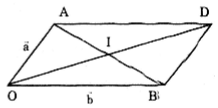
OADB là hình bình hành

\(\Leftrightarrow \overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OD}\)

\(\Leftrightarrow \overrightarrow{OA}+\overrightarrow{OB} =2 \overrightarrow{OI}\) (I là tâm hình bình hành)

\(\Leftrightarrow \overrightarrow{OI}=\frac{1}{2}(\vec{a}+\vec{b})=(0;1;0)\)

Vậy I(0; 1; 0)

⇒ Chọn đáp án A.

Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1;0;0); B(0;1;0); C(0;0;1); D(1;1;1).

Trong các mệnh đề sau, mệnh đề nào sai?

(A) Bốn điểm A, B, C, D tạo thành một tứ diện

(B) Tam giác ABD là tam giác đều

(C) \(AB\perp CD\)

(D) Tam giác BCD là tam giác vuông.

Hướng dẫn giải

\(\overrightarrow{BC}=(0;-1;1), \overrightarrow{BD}=(1;0;1); \overrightarrow{CD}=(1;1;0)\)

\(\overrightarrow{BC}. \overrightarrow{BD}\neq 0; \overrightarrow{BC}. \overrightarrow{CD}\neq 0; \overrightarrow{BD}. \overrightarrow{CD}\neq 0\)

Tam giác BCD không vuông 

⇒ Chọn đáp án D.

Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1;0;0); B(0;1;0); C(0;0;1); D(1;1;1).

Gọi M, N lần lượt là trung điểm của AC và CD. Toạ độ điểm G là trung điểm của MN là:

(A) \(G\left ( \frac{1}{3} ; \frac{1}{3}; \frac{1}{3}\right )\)

(B) \(G\left ( \frac{1}{4} ; \frac{1}{4}; \frac{1}{4}\right )\)

(C) \(G\left ( \frac{2}{3};\frac{2}{3};\frac{2}{3} \right )\)

(D) \(G\left ( \frac{1}{2};\frac{1}{2};\frac{1}{2} \right )\)

Hướng dẫn giải

Ta có \(M\left ( \frac{1}{2};\frac{1}{2};0 \right )\) và \(M\left ( \frac{1}{2};\frac{1}{2};1 \right )\)

Trung điểm MN là \(G\left ( \frac{1}{2};\frac{1}{2};\frac{1}{2} \right )\) 

⇒ Chọn đáp án D.

Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1;0;0); B(0;1;0); C(0;0;1); D(1;1;1).

Mặt cầu ngoại tiếp tứ diện ABCD có bán kính là:

(A) \(\frac{\sqrt{3}}{2}\)

(B) \(\sqrt{2}\)

(C) \(\sqrt{3}\)

(D) \(\frac{3}{4}\)

Hướng dẫn giải

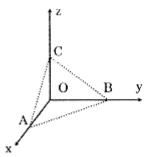
Mặt cầu đi qua 4 điểm A, B, C, D có dạng (S): \(x^2+y^2+z^2-2ax-2by-2cz+d=0\)

Vì A, B, C, D \(\in\) (S) nên \(\left\{\begin{matrix} 1-2a+d=0\\ 1-2b+d=0\\ 1-2c+d=0\\ 3+2(a+b+c)+d=0 \end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} a=\frac{1}{2}\\ \\ b=\frac{1}{2}\\ \\ c=\frac{1}{2}\\ \\ d=0 \end{matrix}\right.\)

Bán kính mặt cầu (S) là \(R=\sqrt{a^2+b^2+c^2-d}=\frac{\sqrt{3}}{2}\)

⇒ Chọn đáp án A

Cho mặt phẳng \((\alpha )\) đi qua điểm M(0;0;-1) và song song với giá của hai vecto \(\vec{a}=(1;-2;3)\) và \(\vec{b}=(3;0;5)\).

Phương trình của mặt phẳng \((\alpha )\) là:

(A) 5x - 2y - 3z - 21 = 0

(B) -5x + 2y + 3z + 3 = 0

(C) 10x - 4y - 6z + 21 = 0

(D) 5x - 2y - 3z + 21 = 0

Hướng dẫn giải

Vecto pháp tuyến của mp \((\alpha )\) là \(\vec{n}=\left [ \vec{a};\vec{b} \right ]=(-10;4;6)\)

Phương trình mp\((\alpha )\):

\(-10(x-0)+4(y-0)+6(z+1)=0\Leftrightarrow -5x+2y+3z+3=0\)

⇒ Chọn đáp án B.

Cho ba điểm A(0; 2; 1), B(3; 0; 1), C(1; 0; 0). Phương trình mặt phẳng (ABC) là:

(A) 2x – 3y – 4z + 2 = 0

(B) 2x + 3y – 4z – 2 = 0

(C) 4x + 6y – 8z + 2 = 0

(D) 2x – 3y – 4z + 1 = 0

Hướng dẫn giải

\(\overrightarrow{AB}=(3;-2;0); \overrightarrow{AC}=(1;-2;-1)\)

Vecto pháp tuyến của mp(ABC) là \(\vec{n}=\left [\overrightarrow{AB};\overrightarrow{AC} \right ]=(2;3;-4)\)

Phương trình mp(ABC) là:

\(2(x-0)+3(y-2)-4(z-1)=0\Leftrightarrow 2x+2y-4z-2=0\)

⇒ Chọn đáp án B.

Gọi \((\alpha )\) là mặt phẳng cắt ba trục toạ độ tại ba điểm M(8; 0; 0), N(0; -2; 0), P(0; 0; 4). Phương trình của \((\alpha )\) là:

(A) \(\frac{x}{8}-\frac{y}{-2}+\frac{z}{4}=0\)

(B) \(\frac{x}{4}+\frac{y}{-1}+\frac{z}{2}=0\)

(C) \(x-4y+2z=0\)

(D) \(x-4y+2z-8=0\)

Hướng dẫn giải

Phương trình mp\((\alpha )\) là:

\(\frac{x}{8}+\frac{y}{-2}+\frac{z}{4}=1\Leftrightarrow x-4y+2z-8=0\)

⇒ Chọn đáp án C.

Cho ba mặt phẳng

\((\alpha ): x+y+2z+1=0\)

\((\beta ): x+y-z+2=0\)

\((\gamma): x-y+5=0\)

Trong các mệnh đề sau, mệnh đề nào sai?

(A) \((\alpha )\perp (\beta )\)

(B) \((\gamma )\perp (\beta )\)

(C) \((\alpha ) // (\gamma )\)

(D) \((\alpha ) \perp (\gamma )\)

Hướng dẫn giải

\((\alpha )\) có vecto pháp tuyến \(\vec{n_\alpha }=(1;1;2)\)

\((\gamma )\) có vecto pháp tuyến \(\vec{n_\gamma }=(1;-1;0)\)

\(\vec{n_\alpha }\) và \(\vec{n_\gamma }\) không cùng phương nên \((\alpha )\) không song song với \((\gamma )\).

⇒ Chọn đáp án C

Cho đường thẳng \(\Delta\) đi qua điểm M(2; 0; -1) và có vecto chỉ phương \(\vec{a}=(4;-6;2)\). Phương trình tham số của đường thẳng \(\Delta\) là:

(A) \(\left\{\begin{matrix} x=-2+4t\\ y=-6t\\ z=1+2t \end{matrix}\right.\)

(B) \(\left\{\begin{matrix} x=-2+2t\\ y=-3t\\ z=1+t \end{matrix}\right.\)

(C) \(\left\{\begin{matrix} x=2+2t\\ y=-3t\\ z=-1+t \end{matrix}\right.\)

(D) \(\left\{\begin{matrix} x=4+2t\\ y=-6-3t\\ z=2+t \end{matrix}\right.\)

Hướng dẫn giải

Ta có: \(\vec{a}=2\vec{a'}\) với \(\vec{a'}=(2;-3;1)\)

Phương trình tham số của \(\Delta\) là: \(\left\{\begin{matrix} x=2+2t\\ y=-3t\\ z=-1+t \end{matrix}\right.\)

⇒ Chọn đáp án C

Cho d là đường thẳng đi qua điểm A(1;2;3) và vuông góc với mặt phẳng \((\alpha ):4x+3y-7z+1=0\)

Phương trình tham số của d là:

(A) \(\left\{\begin{matrix} x=-1+4t\\ y=-2+3t\\ z=-3-7t \end{matrix}\right.\)

(B) \(\left\{\begin{matrix} x=1+4t\\ y=2+3t\\ z=3-7t \end{matrix}\right.\)

(C) \(\left\{\begin{matrix} x=1+3t\\ y=2-4t\\ z=3-7t \end{matrix}\right.\)

(D) \(\left\{\begin{matrix} x=-1+8t\\ y=-2+6t\\ z=-3-14t \end{matrix}\right.\)

Hướng dẫn giải

Vecto pháp tuyến của \((\alpha )\) là \(\vec{n}=(4;3;-7)\), d vuông góc với \((\alpha )\) thì d có vecto chỉ phương \(\vec{a_d}=\vec{n}=(4;3;-7)\)

Phương trình tham số của d là: \(\left\{\begin{matrix} x=1+4t\\ y=2+3t\\ z=3-7t \end{matrix}\right.\)

⇒ Chọn đáp án B

Cho hai đường thẳng: \(d_1:\left\{\begin{matrix} x=1+2t\\ y=2+3t\\ z=3+4t \end{matrix}\right.\) và \(d_2:\left\{\begin{matrix} x=3+4t'\\ y=5+6t'\\ z=7+8t' \end{matrix}\right.\)

Trong các mệnh đề sau, mệnh đề nào đúng?

(A) \(d_1\perp d_2\)

(B) \(d_1 // d_2\)

(C) \(d_1 \equiv d_2\)

(D) \(d_1\) và \(d_2\) chéo nhau.

Hướng dẫn giải

\(d_1\) và \(d_2\)  lần lượt có vecto chỉ phương là:

\(\vec{a}_1=(2;3;4)\) và \(\vec{a}_2=(4;6;8)\)

Ta có \(\vec{a}_1\) cùng phương \(\vec{a}_2\)

\(d_1\) qua \(M_0(1;2;3)\in d_2\) (ứng với \(t'=-\frac{1}{2}\))

Vậy \(d_1 \equiv d_2\)

⇒ Chọn đáp án C.

Cho mặt phẳng \((\alpha ): 2x+y+3z+1=0\) và đường thẳng d có phương trình tham số: \(\left\{\begin{matrix} x=-3+t\\ y=2-2t\\ z=1 \end{matrix}\right.\). Trong các mệnh đề sau, mệnh đề nào đúng? 

(A) \(d\perp (\alpha )\)

(B) \(d\) cắt \((\alpha )\)

(C) \(d\) // \((\alpha )\)

(D) \(d \subset (\alpha )\)

Hướng dẫn giải

Vecto pháp tuyến của \((\alpha )\) là \(\vec{n}=(2;1;3)\)

Vecto chỉ phương của d là \(\vec{a}=(1;-2;0)\)

Ta có \(\vec{n}.\vec{a}=2-2=0\)

d đi qua \(M_0(-3;2;1)\in (\alpha )\) nên \(d\subset (\alpha )\)

⇒ Chọn đáp án D.

Cho (S) là mặt cầu tâm I(2;1;-1) và tiếp tục với mặt phẳng \((\alpha)\) có phương trình: \(2x-2y-z+3=0\).

Bán kính của (S) là:

(A) 2

(B) \(\frac{2}{3}\)

(C) \(\frac{4}{3}\)

(D) \(\frac{2}{9}\)

Hướng dẫn giải

\(R=d(I,(\alpha ))=\frac{\left | 2.2-2.1+1+3 \right |} {\sqrt{2^2+(-2)^2+(-1)^2}}=\frac{6}{3}=2\)

⇒ Chọn đáp án A