Giải bài tập SBT Vật Lý 11 Bài tập cuối chương VII: Mắt - Các dụng cụ quang
Hướng dẫn giải bài tập Bài tập cuối chương VII: Mắt - Các dụng cụ quang sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SBT Lý 11. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.
Mục lục nội dung
1. Giải bài VII.1 trang 94 SBT Vật Lý 11
2. Giải bài VII.2 trang 94 SBT Vật Lý 11
3. Giải bài VII.3 trang 94 SBT Vật Lý 11
4. Giải bài VII.4 trang 95 SBT Vật Lý 11
5. Giải bài VII.5 trang 95 SBT Vật Lý 11
6. Giải bài VII.6 trang 96 SBT Vật Lý 11
7. Giải bài VII.7 trang 96 SBT Vật Lý 11
8. Giải bài VII.8 trang 96 SBT Vật Lý 11

Giải bài tập SBT Vật Lý 11 Bài tập cuối chương VII: Mắt - Các dụng cụ quang
1. Giải bài VII.1 trang 94 SBT Vật Lý 11
Ga-li-lê là người đầu tiên chế tạo kính thiên văn để quan sát bầu trời. Nhà bác học này có sáng kiến dùng thấu kính hội tụ làm vật kính và thấu kính phân kì làm thị kính. Có hai phiên bản:
Phiên bản đầu gồm thấu kính hội tụ tiêu cự f1=1,33m và thấu kính phân kì tiêu cự f2=−94mm
Phiên bản thứ hai gồm thấu kính hội tụ tiêu cự f1=980mm và thấu kính phân kì tiêu cự f2=−47,5mm
Bằng cách lập công thức tính số bội giác của kính thiên văn khi ngắm chừng ở vô cực, hãy cho biết thông số này của kính thiên văn ở phiên bản thứ hai lớn gấp bao nhiêu lần phiên bản đầu
A. 3 lần
B. 2,5 lần
C. 2 lần
D. 1,5 lần
Phương pháp giải
Áp dụng công thức: G=f1/f2 để tính số bội giác của kính thiên văn
Hướng dẫn giải
- Ta có:
G1=f1f2=1,33.10394=14,14G2=f1f2=98047,5=20,63⇒G2=1,5G1
- Chọn đáp án D
2. Giải bài VII.2 trang 94 SBT Vật Lý 11
Một người nhìn trong không khí thì không thấy rõ các vật ở xa. Lặn xuống nước hồ bơi lặng yên thì người này lại nhìn thấy các vật ở xa. Có thể kết luận ra sao về mắt người này?
A. Mắt cận.
B. Mắt viễn.
C. Mắt bình thường (không tật).
D. Mắt bình thường nhưng lớn tuổi (mắt lão).
Phương pháp giải
Mắt cận chỉ nhìn rõ các vật ở gần, không nhìn rõ các vật ở xa mắt
Hướng dẫn giải
- Một người nhìn trong không khí thì không thấy rõ các vật ở xa. Lặn xuống nước hồ bơi lặng yên thì người này lại nhìn thấy các vật ở xa. Có thể kết luận mắt bị cận
- Chọn đáp án A
3. Giải bài VII.3 trang 94 SBT Vật Lý 11
Kính "hai tròng" phần trên có độ tụ D1 > 0 và phần dưới có độ tụ D2 > D1. Kính này dùng cho người có mắt thuộc loại nào sau đây ?
A. Mắt lão.
B. Mắt viễn
C. Mắt lão và viễn.
D. Mắt lão và cận.
Phương pháp giải
Người có mắt lão và viễn thường sử dụng kính "hai tròng" phần trên có độ tụ D1 > 0 và phần dưới có độ tụ D2 > D1
Hướng dẫn giải
- Kính "hai tròng" phần trên có độ tụ D1 > 0 và phần dưới có độ tụ D2 > D1. Kính này dùng cho người có mắt lão và viễn.
- Chọn đáp án C
4. Giải bài VII.4 trang 95 SBT Vật Lý 11
Bộ phận có cấu tạo giống nhau ở kính thiên văn và kính hiển vi là gì ?
A. Vật kính.
B. Thị kính.
C. Vật kính của kính hiển vi và thị kính của kính thiên văn.
D. Không có.
Phương pháp giải
Kính thiên văn và kính hiển vi đều có thị kính là kính lúp
Hướng dẫn giải
- Bộ phận có cấu tạo giống nhau ở kính thiên văn và kính hiển vi là thị kính vì đều là kính lúp.
- Chọn đáp án B
5. Giải bài VII.5 trang 95 SBT Vật Lý 11
Trong công thức về số bội giác của kính hiển vi ngắm chừng ở vô cực G∞=δDf1f2 thì đại lượng δ là gì?
A. Chiều dài của kính.
B. Khoảng cách F1’F2
C. Khoảng cực cận của mắt người quan sát.
D. Một đại lượng khác A, B, C
Phương pháp giải
Để trả lời câu hỏi này cần nắm được các đại lượng trong công thức tính số bội giác
Hướng dẫn giải
- Ta có: G∞=δDf1f2
- Trong đó: δ=F′1F2 được gọi là độ dài quang học .
- Chọn đáp án B
6. Giải bài VII.6 trang 96 SBT Vật Lý 11
Công thức về số bội giác G=f1f2 của kính thiên văn khúc xạ áp dụng được cho trường hợp ngắm chừng nào?
A. Ở điểm cực cận
B. Ở điểm cực viễn.
C. Ở vô cực (hệ vô tiêu)
D. Ở mọi trường hợp ngắm chừng vì vật luôn ở vô cực.
Phương pháp giải
Ngắm chừng ở vô cực ở kính thiên văn sử dụng công thức G=f1f2 để tính số bội giác
Hướng dẫn giải
- Công thức về số bội giác G=f1f2 của kính thiên văn khúc xạ áp dụng được cho trường hợp ngắm chừng ở vô cực.
- Chọn đáp án C
7. Giải bài VII.7 trang 96 SBT Vật Lý 11
Một thấu kính hội tụ có tiêu cự f. Đặt thấu kính này giữa vật AB và màn (song song với vật) sao cho ảnh của AB hiện rõ trên màn và gấp hai lần vật. Để ảnh rõ nét của vật trên màn gấp ba lần vật, phải tăng khoảng cách vật - màn thêm 10 cm. Tính tiêu cự f của thấu kính.
Phương pháp giải
Tính tiêu cự thấu kính theo cách: dựa vào công thức tính độ phóng đại:
k=−d′d=ff−d
- Tìm khoảng cách vật ảnh theo công thức
L1=d1+d′1
- Tìm tiêu cực theo công thức:
−L1=L2=d2+d′2=16f3
Hướng dẫn giải
- Theo đề bài: Ta có khoảng cách của vật và ảnh là:
+k1=−2⇒−d′1d1=−2⇒d′1=2d1+k1=ff−d1=−2⇒d1=3f2
Vậy L1=d1+d′1=9f2
Xem Hình VII.1G.
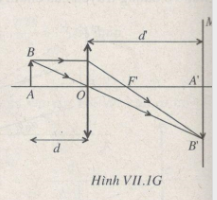
- Tương tự: Ta tính được tiêu cự là:
k2=−3⇒L2=d2+d′2=16f3L2−−L1=10cm⇒5f6=10cm⇒f=12cm.
Vậy tiêu cự f của thấu kính là: 12cm
8. Giải bài VII.8 trang 96 SBT Vật Lý 11
Một thấu kính phân kì L1 có tiêu cự f = -20 cm. S là điểm sáng ở vô cực trên trục chính.
a) Xác định ảnh S1’ tạo bởi L1
b) Ghép thêm thấu kính hội tụ L2 sau L1 đồng trục. Sau L2 đặt một màn vuông góc với trục chính chung và cách L1 một đoạn 100 cm.
Khi tịnh tiến L2, chỉ có một vị trí duy nhất của L2 tạo ảnh sau cùng rõ nét trên màn. Tính f2.
Phương pháp giải
a) Xác định vị trí ảnh theo công thức: d1’ = f1
b) Để tính tiêu cự kính 2 ta làm như sau:
- Áp dụng công thức: d2 + d2’ = l + |f1| = L tính khoảng cách vật và ảnh
- Vì L là hằng số, thay giá trị và giả phương trình để tìm f2
Hướng dẫn giải
a) d1 --> ∞; d1’ = f1 = -20cm
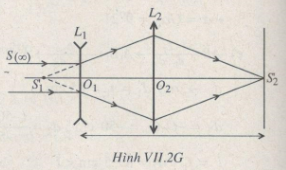
b) Khi S2’ hiện trên màn (Hình VII.2G) ta có:
d2 + d2’ = l + |f1| = L = const
⇒d2+d2f2d2−f2=L⇒d22−Ld2+Lf2=0
Vì chỉ có một vị trí của L2 nên phương trình trên có nghiệm kép.
Δ=L2−4Lf2=0⇒f2=L4=1204=30cm
9. Giải bài VII.9 trang 96 SBT Vật Lý 11
Một mắt cận có điểm CvCv cách mắt 50 cm.
a) Xác định loại và độ tụ của thấu kính mà người cận thị phải đeo lần lượt để có thể nhìn rõ không điều tiết một vật:
- Ở vô cực
- Cách mắt 10 cm.
b) Khi đeo cả hai kính trên đây ghép sát nhau, người cận thị này đọc được một trang sách đặt cách mắt ít nhất 10 cm. Tính khoảng cực cận của mắt cận này. Khi đeo cả hai kính thì người này đọc được sách đặt cách mắt xa nhất là bao nhiêu? ( Quang tâm của mắt và kính trùng nhau).
Phương pháp giải
a)- Tính tiêu cự theo công thức:
+ fk=−OCV đối với vật ở vô cực
+ 1f′k=1d−1OCv đối với vật ở cách xa 10 cm
- Áp dụng công thức: Dk=1/fk để tính độ tụ
b) Sử dụng biểu thức tính tiêu cự của thấu kính tương đương: 1/f=1/fk+1/f′k
- Tính khoảng cực cận theo công thức:
1dmin=1f+1OCc
- Tính vị trí đặt sách xa nhất theo công thức:
1dmax=1f+1OCv
Hướng dẫn giải
a)- Vật ở vô cực:
fk=−OCV=−50cmDk=1fk=−10,5=−2dp
- Vật ở cách xa 10 cm.
1f′k=1d−1OCv=110−150=>f′k=12,5cmD′k=1f′k=10,125=8dp
b) Tiêu cự của thấu kính tương đương:
1f=1fk+1f′k=>fk=503cm
- Khoảng cực cận:
1dmin=1f+1OCc=>OCc=25cm
- Sách đặt xa nhất:
1dmax=1f+1OCv=>dmax=12,5cm
10. Giải bài VII.10 trang 97 SBT Vật Lý 11
Vật kính của một kính hiển vi có tiêu cự f1=1cm ; thị kính có tiêu cự f2=4cm. Độ dài quang học của kính là 16 cm. Người quan sát có mắt không bị tật và có khoảng cực cận là 20 cm.
a) Phải đặt vật trong khoảng nào trước vật kính để người quan sát có thể nhìn thấy ảnh của vật qua kính.
b) Tính số bội giác của ảnh trong trường hợp ngắm chừng ở vô cực.
c) Năng suất phân li của mắt người quan sát là 2'. Tính khoảng cách ngắn nhất giữa hai điểm trên vật mà người quan sát còn phân biệt được ảnh qua kính khi ngắm chừng ở vô cực.
Phương pháp giải
a) Vận dụng lí thuyết và công thức thấu kính để trả lời câu hỏi này
b) Áp dụng công thức:
G=δ.OCcf1.f2 để tính số bội giác
c) Khoảng ngắn nhất mà mắt phân biệt được tính theo công thức:
Δy1’ = f2tanε = f2ε
⇒ Khoảng cách ngắn nhất đó là: Δy=f2ε|k1|
Hướng dẫn giải
a) Khoảng có thể xê dịch vật MN tương ứng với khoảng CV CC có thể sẽ dịch ảnh.
- Sự tạo ảnh của điểm M:
ML1→d1;d1′M1L2→d2;d2′M′≡CV
- Vị trí đặt vật tại M:
d2′=−OCV→∞d2=f2=4cmd1′=l−d2=21−4=17cmd1=17.116≈10,625mm
- Sự tạo ảnh của điểm N:
NL1→d1;d1′N1L2→d2;d2′N′≡CC
- Vị trí đặt vật tại N là:
d2′=−O2CC=−20cmd2=20.424=103cmd1′=l−d2=21−103=533cmd1=100100≈10,6mm
Suy ra: Δd=25.10−6m
b) Ta có: số bội giác của ảnh trong trường hợp ngắm chừng ở vô cực là:
G=δ.OCcf1.f2=80
c) Khi ngắm chừng ở vô cực, ảnh A1’B1’ của vật tạo bởi vật kính ở tại tiêu diện vật của thị kính (Hình 33.1G).
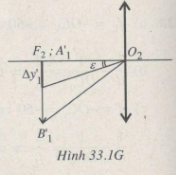
- Khoảng ngắn nhất trên A1’B1’ mà mắt phân biệt được:
Δy1’ = f2tanε = f2ε
- Suy ra khoảng ngắn nhất trên vật:
Δy=f2ε|k1|=4,6.10−416=1,5.10−6m
Tham khảo thêm
- doc Giải bài tập SBT Vật Lí 11 Bài 28: Lăng kính
- doc Giải bài tập SBT Vật Lí 11 Bài 29: Thấu kính mỏng
- doc Giải bài tập SBT Vật Lí 11 Bài 30: Giải bài toán về hệ thấu kính
- doc Giải bài tập SBT Vật Lí 11 Bài 31: Mắt
- doc Giải bài tập SBT Vật Lí 11 Bài 32: Kính lúp
- doc Giải bài tập SBT Vật Lí 11 Bài 33: Kính hiển vi
- doc Giải bài tập SBT Vật Lí 11 Bài 34: Kính thiên văn




