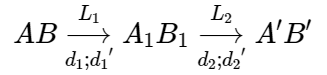Giải bài tập SBT Vật Lí 11 Bài 34: Kính thiên văn
Ban biên tập eLib xin giới thiệu Giải bài tập SBT Vật lý 11 Bài 34 dưới đây để giúp các em có thể rèn luyện kỹ năng làm bài Vật lý liên quan các kiến thức về kính thiên văn. Mời các em cùng tham khảo!
Mục lục nội dung

1. Giải bài 1 trang 93 SBT Vật lý 11
Một người có mắt tốt quan sát một ngôi sao qua kính thiên văn trong trạng thái ngắm chừng ở vô cực .
Chùm tia sáng từ ngôi sao chiếu đến vật kính , khi ló ra khỏi thị kính sẽ là chùm
A. Phân kì
B. Hội tụ
C. Song song
D. Được nêu ở A, B, C tùy theo cấu tạo của kính.
Phương pháp giải
Vận dụng kiến thức về kính thiên văn để trả lời câu hỏi này
Hướng dẫn giải
- Quan sát một ngôi sao qua kính thiên văn trong trạng thái ngắm chừng ở vô cực .Chùm tia sáng từ ngôi sao chiếu đến vật kính , khi ló ra khỏi thị kính sẽ là chùm song song.
- Chọn đáp án: C
2. Giải bài 2 trang 93 SBT Vật lý 11
Ghép ba thấu kính : Một thấu kính phân kì có độ tụ -1 dp và hai thấu kính hội tụ có tiêu cự lần lượt là 50 cm và 10 cm thành một kính thiên văn. Số bội giác lớn nhất của kính thiên văn đó khi ngắm chừng ở vô cực sẽ là bao nhiêu? Chọn đáp số đúng.
A. 10
B. 15
C. 20
D. 5
Phương pháp giải
Sử dụng biểu thức tính độ bội giác khi ngắm chừng ở vô cực:
\({G_{max}} = \frac{{{f_1}}}{{{f_3}}}\)
Hướng dẫn giải
- Số bội giác lớn nhất của kính thiên văn đó khi ngắm chừng ở vô cực sẽ là:
\(\begin{array}{l} {f_1} = \frac{1}{D} = 1m\\ {G_{max}} = \frac{{{f_1}}}{{{f_3}}} = 10 \end{array}\)
- Chọn đáp án: A
3. Giải bài 3 trang 93 SBT Vật lý 11
Người có mắt không bị tật quan sát kính thiên văn ở trạng thái không điều tiết thì có thể kết luận gì về độ dài l của kính và số bội giác G∞?
\(\begin{array}{l} A.\,l = {f_1} - {f_2};{G_\infty } = \frac{{{f_1}}}{{{f_2}}}\\ B.\,l = {f_1} - {f_2};{G_\infty } = \frac{{{f_2}}}{{{f_1}}}\\ C.\,l = {f_1} + {f_2};{G_\infty } = \frac{{{f_2}}}{{{f_1}}}\\ D.\,l = {f_1} + {f_2};{G_\infty } = \frac{{{f_1}}}{{{f_2}}} \end{array}\)
Phương pháp giải
Công thức kính thiên văn khi ngắm chừng ở vô cực:
\(l = {f_1} + {f_2};{G_\infty } = \frac{{{f_1}}}{{{f_2}}}\)
Hướng dẫn giải
- Khi mắt không điều tiết thì ảnh ở vô cực ( ngắm chừng ở vô cực)
⇒ \(l = {f_1} + {f_2};{G_\infty } = \frac{{{f_1}}}{{{f_2}}}\)
- Chọn đáp án D
4. Giải bài 4 trang 93 SBT Vật lý 11
Một người có khoảng cực cận Đ quan sát ảnh của một thiên thể bằng cách ngắm chừng ở cực cận. Số bội giác của kính có biểu thức nào (mắt sát thị kính)?
A. \(\frac{{{f_1}}}{{{f_2}}}\)
B. \(\frac{D}{{{f_1} + {f_2}}}\)
C. \(\frac{{{k_2}{f_1}}}{D}\)
D. Khác A, B, C
Phương pháp giải
Công thức tính độ bội giác:
\(G = \frac{{tan\alpha }}{{tan{\alpha _0}}} = \frac{{{k_2}{f_1}}}{D}\)
Hướng dẫn giải
- Số bội giác là:
\(G = \frac{{tan\alpha }}{{tan{\alpha _0}}} = \frac{{\frac{{{A_2}{B_2}}}{D}}}{{\frac{{{A_1}{B_1}}}{{{f_1}}}}} = \frac{{{k_2}{f_1}}}{D}\)
- Chọn đáp án C
5. Giải bài 5 trang 93 SBT Vật lý 11
Kính thiên văn khúc xạ Y – éc – xơ (Yerkes) có tiêu cự vật kính là 19,8m. Mặt Trăng có góc trông từ Trái Đất là 33’. Ảnh của Mặt Trăng tạo bởi vật kính của kính thiên văn này có độ lớn (tính tròn) là bao nhiêu?
A. 19cm B. 53cm
C. 60cm D. Một trị số khác A, B, C.
Phương pháp giải
Áp dụng công thức:
\(tan\alpha = \frac{{A_1^\prime B_1^\prime }}{{{f_1}}}\)để tính độ cao ảnh
Hướng dẫn giải
- Ta có:
\(tan\alpha = \frac{{A_1^\prime B_1^\prime }}{{{f_1}}} = > A_1^\prime B_1^\prime = 19cm\)
- Chọn đáp án A
6. Giải bài 6 trang 94 SBT Vật lý 11
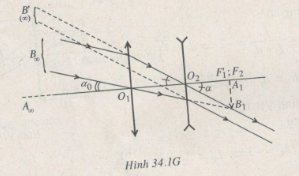
Để làm giảm chiều dài của kính và đồng thời tạo ảnh thuận chiều, kính thiên văn được biến đổi bằng cách dùng thấu kính phân kỳ làm thị kính. Kính được dùng làm ống nhòm,… Cho biết vật ở vô cực và ảnh cũng được tạo ra ở vô cực. Vẽ đường truyền của chùm tia sáng.
Phương pháp giải
Vận dụng kiến thức về đường truyền của tia sáng khi đi qua thấu kính để vẽ hình
Hướng dẫn giải
Vẽ đường truyền của chùm tia sáng: xem Hình 34.1G.
7. Giải bài 7 trang 94 SBT Vật lý 11
Vật kính của kính thiên văn là một thấu kính hội tụ L1 có tiêu cự lớn; thị kính là một thấu kính hội tụ L2 có tiêu cự nhỏ.
a) Một người mắt không có tật, dùng kính thiên văn này để quan sát Mặt Trăng ở trạng thái không điều tiết. Khi đó khoảng cách giữa vật kính và thị kính là 90cm. Số bội giác của ảnh là 17. Tính các tiêu cự của vật kính và thị kính.
b) Góc trông của Mặt Trăng từ Trái Đất là 33’ (1’ = 1/3500rad). Tính đường kính ảnh của Mặt Trăng tạo bởi vật kính và góc trông ảnh của Mặt Trăng qua thị kính.
c) Một người cận thị có điểm cực viễn CV cách mắt 50cm, không đeo kính cận, quan sát Mặt Trăng qua kính thiên văn nói trên. Mắt đặt sát thị kính. Người này phải dịch chuyển thị kính như thế nào để khi quan sát mắt không phải điều tiết?
Phương pháp giải
a) Tính tiêu cự vật kính và thị kính theo công thức:
G=f1/f2 ; O1O2 = f1 + f2
b)- Áp dụng công thức:
\(\begin{array}{l} {A_1}{B_1} = {f_1}{\alpha _0} \end{array}\) để tính đường kính ảnh
- Áp dụng công thức:
\(\begin{array}{l} \alpha = G{\alpha _0} \end{array}\)để tính góc trông ảnh
c) Vận dụng lí thuyết về sự tạo ảnh qua kính thiên văn để giải
Hướng dẫn giải
a) Theo đề bài:
Ta có tiêu cự của vật kính và thị kính là:
l = O1O2 = f1 + f2 = 90cm; G=f1/f2=17
=> f1 = 85cm; f2 = 5cm
b) Đường kính ảnh của Mặt Trăng tạo bởi vật kính và góc trông ảnh của Mặt Trăng qua thị kính là:
\(\begin{array}{l} {A_1}{B_1} = {f_1}{\alpha _0} = \frac{{85.33}}{{3500}} \approx 0,8cm = 8mm\\ \alpha = G{\alpha _0} = {9^0}{21^\prime } \end{array}\)
c) Sơ đồ tạo ảnh:
\(\begin{array}{l} {d_1} \to \infty ;{d_1}\prime = {f_1} = 85cm\\ {d_2}\prime = - {O_2}{C_V} = - 50cm;\\ {d_2} = \frac{{( - 50).5}}{{ - 55}} \approx 4,55cm\\ l\prime = {f_1} + {d_2} = 89,5cm < l \end{array}\)
Dời thị kính 0,5cm tới gần vật kính hơn.
Tham khảo thêm
- doc Giải bài tập SBT Vật Lí 11 Bài 28: Lăng kính
- doc Giải bài tập SBT Vật Lí 11 Bài 29: Thấu kính mỏng
- doc Giải bài tập SBT Vật Lí 11 Bài 30: Giải bài toán về hệ thấu kính
- doc Giải bài tập SBT Vật Lí 11 Bài 31: Mắt
- doc Giải bài tập SBT Vật Lí 11 Bài 32: Kính lúp
- doc Giải bài tập SBT Vật Lí 11 Bài 33: Kính hiển vi
- doc Giải bài tập SBT Vật Lý 11 Bài tập cuối chương VII: Mắt - Các dụng cụ quang