Lý 8 Bài 3: Chuyển động đều- Chuyển động không đều

- Chuyển động đều là chuyển động mà vận tốc có độ lớn không thay đổi theo thời gian.

+ Ví dụ:

• Chuyển động của đầu cánh quạt khi quạt quay ổn định

• Chuyển động của vệ tinh nhân tạo bay xung quanh Trái Đất

- Chuyển động không đều là chuyển động mà vận tốc có độ lớn thay đổi theo thời gian.

• Ví dụ: Chuyển động của xe ô tô trên đường, lúc nhanh lúc chậm khác nhau, vận tốc của ô tô thay đổi theo thời gian ⇨ chuyển động đó là chuyển động không đều.

- Vận tốc trung bình của một chuyển động không đều trên một quãng đường đựơc tính bằng công thức: \({v_{tb}} = \frac{s}{t} \)

+ Trong đó:

• s là quãng đường đi được

• t là thời gian đi hết quãng đường đó.

Chú ý: Khi nói đến vận tốc trung bình phải nói rõ vận tốc trung bình đó tính trên đoạn đường nào vì trên các đoạn đường khác nhau, vận tốc trung bình có thể khác nhau.

a) Tính vận tốc trung bình của chuyển động không đều

- Công thức: \({v_{tb}} = \frac{{{s_1} + {s_2} + ...{s_n}}}{{{t_1} + {t_2} + ...{t_n}}} \)

• Trong đó: s_1, s₂…s_n và t₁, t₂…tn là những quãng đường đi được và thời gian để đi hết quãng đường đó.

Chú ý: Vận tốc trung bình hoàn toàn khác với trung bình cộng vận tốc: \({v_{tb}} \ne \frac{{{v_1} + {v_2} + ... + {v_n}}}{n} \)

b) Phương pháp giải bài toán bằng đồ thị

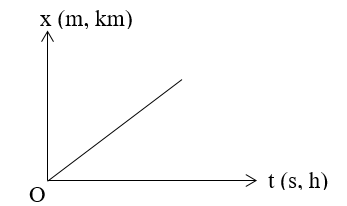
- Thường chọn gốc tọa độ trùng với điểm xuất phát của một trong hai chuyển động. Chọn trục tung là Ox (biểu diễn quãng đường đi được), trục hoành là Ot (biểu diễn thời gian).

- Đồ thị là một đường thẳng có thể đi qua gốc tọa độ O hoặc không, tùy thuộc vào ta chọn mốc tọa độ và mốc thời gian.

- Viết phương trình đường đi của mỗi chuyển động có dạng: x = x_o + s = x_o + v(t – t_o)

+ Trong đó:

• xo là tọa độ ban đầu của vật.

• t_o là thời điểm xuất phát.

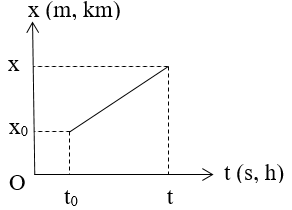
- Vẽ đồ thị của mỗi chuyển động. Dựa vào giao điểm của các đồ thị để tìm thời điểm và vị trí gặp nhau của các chuyển động.

Một ô tô lên dốc với vận tốc 16 km/h, khi xuống lại dốc đó, ô tô này chuyển động nhanh gấp đôi khi lên dốc. Vận tốc trung bình của ô tô trong cả hai đoạn đường lên dốc và xuống dốc là bao nhiêu?

Hướng dẫn giải

Gọi s là độ dài quãng đường dốc

\({t_1} = \frac{s}{{16}} \) là thời gian lên dốc

\({t_2} = \frac{s}{{32}} \) là thời gian xuống dốc

Vận tốc trung bình của ô tô trong cả hai đoạn đường là:

\(v = \frac{{2s}}{{{t_1} + {t_2}}} = \frac{{2{\rm{s}}}}{{\frac{s}{{16}} + \frac{s}{{32}}}} = 21,33\,km/h\ \)

Một máy bay chở hành khách bay giữa hai thành phố A và B. Khi xuôi gió thời gian bay là 1h30’, còn khi ngược gió thời gian bay là 1h45’. Biết vận tốc gió luôn không đổi là 10 m/s. Vận tốc của máy bay lúc không có gió là bao nhiêu?

Hướng dẫn giải

Gọi v là vận tốc của máy bay, v_g là vận tốc của gió.

t₁, t₂ lần lượt là thời gian lúc xuôi gió và ngược gió.

t₁ = 1h 30’ = 5400 s

t₂ = 1h 45’ = 6300 s

Do quãng đường của máy bay bay đi lúc xuôi gió và ngược gió là bằng nhau

⇒ t₁(v + v_g) = t₂(v – v_g)

\(\frac{{{t_1}}}{{{t_2}}} = \frac{{v + {v_g}}}{{v - {v_g}}} \)

\(\Rightarrow \frac{{5400}}{{6300}} = \frac{{v + 10}}{{v - 10}} \)

⇒ 5400.(v – 10) = 6300.(v + 10)

⇒ 900.v = 63000 + 54000 = 117000 ⇒ v = 130 m/s = 468 km/h

Câu 1: Một máy bay chở hành khách bay giữa hai thành phố A và B. Khi xuôi gió thời gian bay là 1h30’, còn khi ngược gió thời gian bay là 1h45’. Biết vận tốc gió luôn không đổi là 10 m/s. Vận tốc của máy bay lúc không có gió là bao nhiêu?

Câu 2: Một người đua xe đạp, trong nửa quãng đường đầu người đó đi với vận tốc 20 km/h. Tính vận tốc của người đó đi trong nửa đoạn đường còn lại. Biết rằng vận tốc trung bình trong cả đoạn đường là 23 km/h.

Câu 3: Người đi xe máy trên đoạn đường AB. Nửa đoạn đường đầu người ấy đi với vận tốc 30 km/h. Trong nửa thời gian còn lại đi với vận tốc 25 km/h. Cuối cùng người ấy đi với vận tốc 15 km/h. Tính vận tốc trung bình trên cả đoạn đường AB.

Câu 4: Một chiếc thuyền máy chuyển động đều trên dòng sông. Vận tốc của thuyền khi xuôi dòng là 20 km/h và khi ngược dòng là 15 km/h.

a) Nếu thuyền không nổ máy thì quãng đường mà thuyền trôi theo dòng nước trong thời gian 30 phút là bao nhiêu?

b) Giả sử mặt nước đứng yên, thuyền có nổ máy thì vận tốc của thuyền lúc đó là bao nhiêu?

Câu 1: Khi nói đến vận tốc của các phương tiện giao thông như xe máy, ô tô, xe lửa, máy bay… người ta nói đến

A. vận tốc tức thời.

B. vận tốc trung bình.

C. vận tốc lớn nhất có thể đạt được của phương tiện đó.

D. vận tốc nhỏ nhất có thể đạt được của phương tiện đó.

Câu 2: Chuyển động đều là chuyển động có độ lớn vận tốc

A. không đổi trong suốt thời gian vật chuyển động.

B. không đổi trong suốt quãng đường đi.

C. luôn giữ không đổi, còn hướng của vận tốc có thể thay đổi.

D. Các câu A, B, C đều đúng.

Câu 3: Chuyển động nào sau đây là chuyển động đều?

A. Vận động viên trượt tuyết từ dốc núi xuống.

B. Vận động viên chạy 100 m đang về đích.

C. Máy bay bay từ Hà Nội vào Hồ Chí Minh.

D. Không có chuyển động nào kể trên là chuyển động đều.

Câu 4: Một người đi quãng đường s₁ với vận tốc v₁ hết t₁ giây, đi quãng đường tiếp theo s2 với vận tốc v₂ hết t₂ giây. Dùng công thức nào để tính vận tốc trung bình của người này trên cả hai quãng đường s₁ và s₂?

A. \({v_{tb}} = \frac{{{v_1} + {v_2}}}{2} \)

B. \({v_{tb}} = \frac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} \)

C. \({v_{tb}} = \frac{{{s_1}}}{{{t_1}}} + \frac{{{s_2}}}{{{t_2}}} \)

D. Cả B và C đều đúng

Qua bài học này, các em sẽ được làm quen với các kiến thức liên quan đến Chuyển động đều-Chuyển động không đều cùng với các bài tập liên quan theo nhiều cấp độ từ dễ đến khó…, các em cần phải nắm được: 

• Nêu được những ví dụ về chuyển động không đều thường gặp.
• Vận dụng để tính vận tốc trung bình trên một đoạn đường.
• Phát biểu được định nghĩa chuyển động đều và nêu được những thí dụ về chuyển động đều.