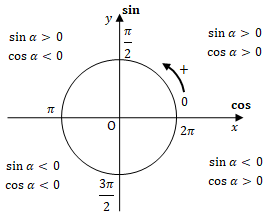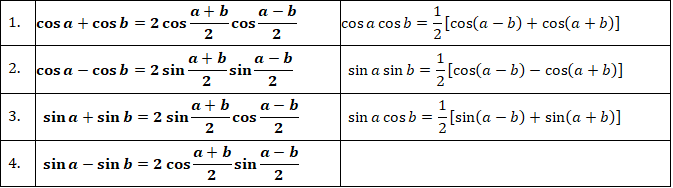Toán 10 Chương 6 Ôn tập chương 6 Cung Góc lượng giác và Công thức lượng giác
Elib đã biên soạn và tổng hợp để giới thiệu đến các em nội dung bài giảng Ôn tập chương 6 Cung Góc lượng giác và Công thức lượng giác. Bài giảng giúp các em nắm vững lý thuyết bài học, kèm theo đó là những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em hiểu bài hơn. Mời các em cùng theo dõi.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Quan hệ giữa độ và rađian
\({180^ \circ } = \pi {\rm{ }}rad\)
Các góc đặc biệt \(0;\dfrac{\pi }{6};\dfrac{\pi }{4};\dfrac{\pi }{3};\dfrac{\pi }{2};\pi \)
1.2. Giá trị lượng giác của \(\alpha \)
\(\begin{array}{l}
1.\sin \left( {\alpha + k2\pi } \right) = \sin \alpha \;\;\;\left( {k \in Z} \right)\\
\cos \left( {\alpha + k2\pi } \right) = \cos \alpha \;\;\;\left( {k \in Z} \right)\\
\tan \left( {\alpha + k\pi } \right)\;\;\; = \tan \alpha \;\;\;\left( {k \in Z} \right)\\
\cot \left( {\alpha + k\pi } \right)\;\;\; = \cot \alpha \;\;\;\left( {k \in Z} \right)
\end{array}\)
\(2.\left| {\sin \alpha } \right| \le 1\;\;\;\;\;\left| {\cos \alpha } \right| \le 1\)
1.3. Công thức lượng giác cơ bản
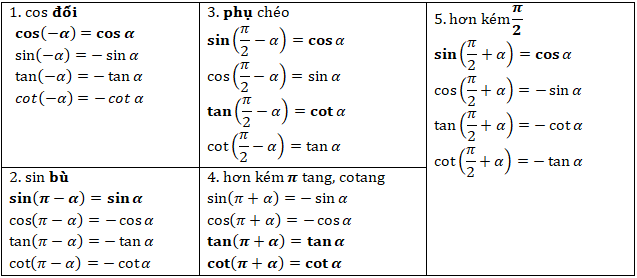
1.4. Công thức cung liên kết
1.5. Công thức cộng
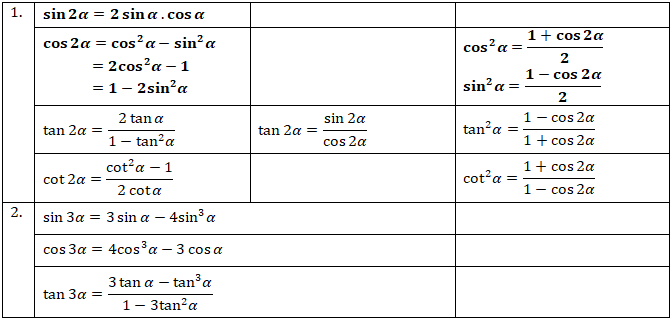
1.6. Công thức nhân đôi - nhân ba - hạ bậc
1.7. Công thức biến đổi tổng thành tích - tích thành tổng
2. Bài tập minh hoạ
Câu 1: Không dùng bảng hay máy tính cầm tay, chứng minh rằng
\(\sin 15^\circ + \sin 75^\circ > 1\) .
Hướng dẫn giải
Ta có:
\({\left( {\sin 15^\circ + sin75^\circ } \right)^2}\)
\(= {\left( {\sin 15^\circ + \cos 15^\circ } \right)^2}\)
\(\begin{array}{l} = {\sin ^2}15^\circ + {\cos ^2}15^\circ + 2\sin 15^\circ \cos 15^\circ \\ = 1 + \sin 30^\circ = \dfrac{3}{2} > 1\end{array}\)
Mà \(\sin 15^\circ + \sin 75^\circ > 0\) nên suy ra \(\sin 15^\circ + \sin 75^\circ > 1\).
Câu 2: Cho \(\sin \alpha + \cos \alpha = \dfrac{1}{2}\) . Tính \({\sin ^3}\alpha + {\cos ^3}\alpha \)
Hướng dẫn giải
Ta có: \(\sin \alpha + \cos \alpha = \dfrac{1}{2} \)
\(\Rightarrow {\left( {\sin \alpha + \cos \alpha } \right)^2} = \dfrac{1}{4}\)
\( \Rightarrow 1 + 2\sin \alpha \cos \alpha = \dfrac{1}{4}\)
\( \Rightarrow \sin \alpha \cos \alpha = - \dfrac{3}{8}\)
Do đó
\(\begin{array}{l}{\sin ^3}\alpha + {\cos ^3}\alpha \\= {\left( {\sin \alpha + \cos \alpha } \right)^3} - 3\sin \alpha \cos \alpha \left( {\sin \alpha + \cos \alpha } \right)\\ = \dfrac{1}{8} + \dfrac{9}{{16}} = \dfrac{{11}}{6}.\end{array}\)
Câu 3: Cho \(\pi < \alpha < \dfrac{{3\pi }}{2}\) và \(\cos \alpha = - \dfrac{9}{{41}}\) . Tính \(\tan \left( {\alpha - \dfrac{{3\pi }}{4}} \right)\) .
Hướng dẫn giải
a có \({\tan ^2}\alpha = \dfrac{1}{{{{\cos }^2}\alpha }} - 1 = \dfrac{{1681}}{{81}} - 1\)\(\; = \dfrac{{1600}}{{81}}\).
Mà \(\pi < \alpha < \dfrac{{3\pi }}{2}\) nên \(\tan \alpha < 0\). Suy ra \(\tan \alpha = \dfrac{{40}}{9}\).
Do đó
\(\tan \left( {\alpha - \dfrac{{3\pi }}{4}} \right) = \dfrac{{\tan \alpha - \tan \dfrac{{3\pi }}{4}}}{{1 + \tan \alpha \tan \dfrac{{3\pi }}{4}}} \)
\(= \dfrac{{\tan \alpha + 1}}{{1 - \tan \alpha }} = \dfrac{{\dfrac{{40}}{9} + 1}}{{1 - \dfrac{{40}}{9}}} = - \dfrac{{49}}{{31}}\).
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Chứng minh các đồng nhất thức
\(\begin{array}{l}
a)\frac{{1 - \cos x + \cos 2x}}{{\sin 2x - \sin x}} = \cot x\\
b)\frac{{\sin x + \sin \frac{x}{2}}}{{1 + \cos x + \cos \frac{x}{2}}} = \tan \frac{x}{2}\\
c)\frac{{2\cos 2x - \sin 4x}}{{2\cos 2x + \sin 4x}} = {\tan ^2}\left( {\frac{\pi }{4} - x} \right)\\
d)\tan x - \tan y = \frac{{\sin \left( {x - y} \right)}}{{\cos x.\cos y}}
\end{array}\)
Câu 2: Chứng minh các biểu thức sau không phụ thuộc x
\(\begin{array}{l}
a)A = \sin \left( {\frac{\pi }{4} + x} \right) - \cos \left( {\frac{\pi }{4} - x} \right)\\
b)B = \cos \left( {\frac{\pi }{6} - x} \right) - \sin \left( {\frac{\pi }{3} + x} \right)\\
c)C = {\sin ^2}x + \cos \left( {\frac{\pi }{3} - x} \right)\cos \left( {\frac{\pi }{3} + x} \right)\\
d)D = \frac{{1 - \cos 2x + \sin 2x}}{{1 + \cos 2x + \sin 2x}}.\cot x
\end{array}\)
3.2. Bài tập trắc nghiệm
Câu 1: Cho tam giác ABC thỏa mãn \(\cos 2A + \cos 2B + \cos 2C = - 1\) thì :
A. Tam giác ABC vuông
B. Không tồn tại tam giác ABC
C. Tam giác ABC đều
D. Tam giác ABC cân
Câu 2: Tính giá trị biểu thức \(S = \;\frac{{4 - 2{{\tan }^2}{{45}^0} + {{\cot }^4}{{60}^0}}}{{3{{\sin }^3}{{90}^0} - 4{{\cos }^2}{{60}^0} + 4\cot {{45}^0}}}\)
A. -1
B. \(1 + \frac{1}{{\sqrt 3 }}\)
C. \(\frac{{19}}{{54}}\)
D. \( - \frac{{25}}{2}\)
Câu 3: Đơn giản biểu thức \(D = \tan x + \frac{{\cos x}}{{1 + \sin x}}\)
A. \(\frac{1}{{\sin x}}\)
B. \(\frac{1}{{\cos x}}\)
C. cosx
D. sinx
Câu 4: Đơn giản biểu thức \(E = \cot x + \frac{{\sin x}}{{1 + \cos x}}\)
A. \(\frac{1}{{\sin x}}\)
B. \(\frac{1}{{\cos x}}\)
C. cosx
D. sinx
Câu 5: Tính giá trị của biểu thức \(P = \tan \alpha - \tan \alpha {\sin ^2}\alpha \) nếu cho \(\cos \alpha = - \frac{4}{5}\;\quad (\;\pi < \;\alpha \; < \;\frac{{3\pi }}{2}\;)\)
A. \(\frac{{12}}{{25}}\)
B. \( - \sqrt 3 \)
C. \(\frac{1}{3}\)
D. 1
3.3. Trắc nghiệm Online
Các em hãy luyện tập bài trắc nghiệm Ôn tập chương 6 Cung Góc lượng giác và Công thức lượng giác Toán 10 sau để nắm rõ thêm kiến thức bài học.
4. Kết luận
Qua bài học này các em cần đạt được những yêu cầu sau:
- Ôn tập và hệ thống lại kiến thức của toàn chương
- Nắm chắc các kiến thức lý thuyết đã học để làm được các bài tập liên quan.
Tham khảo thêm
- doc Toán 10 Chương 6 Bài 1: Cung và góc lượng giác
- doc Toán 10 Chương 6 Bài 2: Giá trị lượng giác của một cung
- doc Toán 10 Chương 6 Bài 3: Công thức lượng giác