Toán 10 Chương 6 Bài 2: Giá trị lượng giác của một cung
Mời các em cùng tham khảo nội dung bài giảng Giá trị lượng giác của một cung do eLib biên soạn và tổng hợp dưới đây. Bài giảng giúp các em nắm vững lý thuyết bài học, thêm vào đó là những bài tập minh họa có hướng dẫn giải chi tiết sẽ giúp các em dễ dàng làm được các dạng bài tập ở phần này.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Giá trị lượng giác của cung \(\alpha \)
1.1.1. Định nghĩa
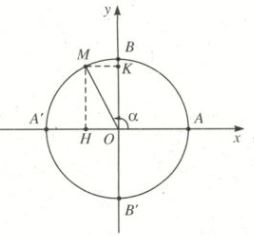
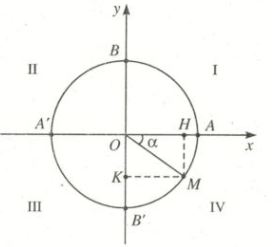
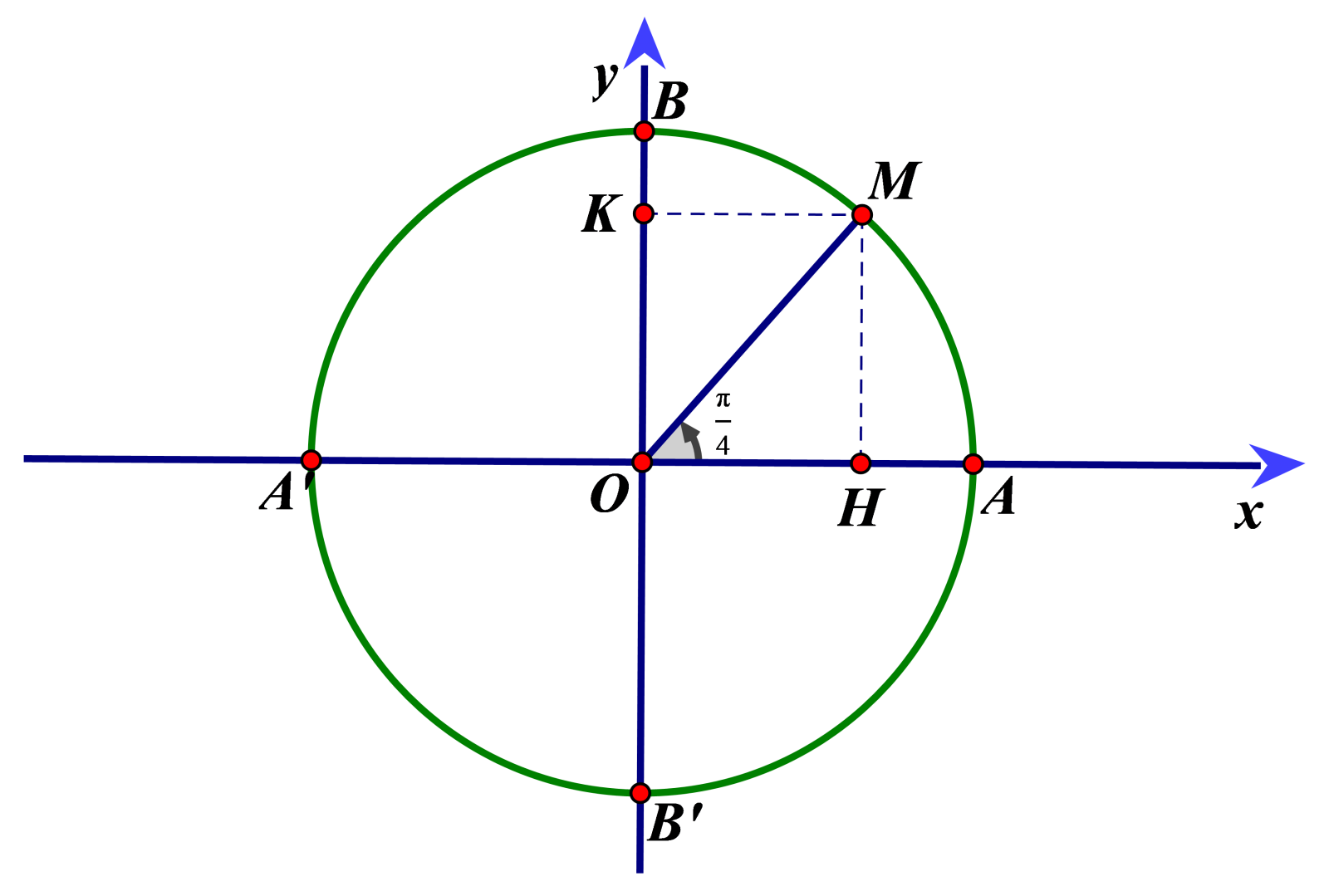
Trên đường tròn lượng giác, cho điểm \(M\left( {{x_o},{y_o}} \right)\) sao cho cung lượng giác AM có sđ\(AM = \alpha \). Khi đó:
\(\begin{array}{l}
\sin \alpha = \overline {OK} = {y_0}\\
\cos \alpha = \overline {OH} = {x_0}\\
\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}{\rm{ }}\left( {\cos \alpha \ne 0} \right)\\
\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}{\rm{ }}\left( {\sin \alpha \ne 0} \right)
\end{array}\)
Định nghĩa: Các giá trị \(\sin \alpha ,\cos \alpha {\rm{, tan}}\alpha {\rm{, cot}}\alpha \) được gọi là các giá trị lượng giác của cung . Ta cũng gọi trục tung là trục sin, còn trục hoành là trục côsin.
Chú ý:
- Các định nghĩa trên cũng áp dụng cho các góc lượng giác.
- Nếu \({0^ \circ } \le \alpha \le {180^ \circ }\) thì các giá trị lượng giác của góc \(\alpha \) chính là các giá trị lượng giác của góc đó.
1.1.2. Hệ quả
1) \(\sin \alpha \) và \(\cos \alpha \) xác định với mọi \(\alpha \in R\).
\(\begin{array}{l}
\sin \left( {\alpha + k2\pi } \right) = \sin \alpha ,\forall k \in Z\\
\cos \left( {\alpha + k2\pi } \right) = \cos \alpha ,\forall k \in Z
\end{array}\)
2) \( - 1 \le \sin \alpha \le 1, - 1 \le \cos \alpha \le 1\)
3) Với mọi \(m \in R\) mà \( - 1 \le m \le 1\) đều tồn tại \(\alpha \) và \(\beta \) sao cho \(\sin \alpha = m\) và \(\cos \alpha = m\)
4) \(\tan \alpha \) xác định với mọi \(\alpha \ne \frac{\pi }{2} + k\pi {\rm{ }}\left( {k \in Z} \right)\)
5) \(\cot \alpha \) xác định với mọi \(\alpha \ne k\pi {\rm{ }}\left( {k \in Z} \right)\)
6) Bảng xác định dấu của các giá trị lượng giác
.png)
1.1.3. Giá trị lượng giác của các cung đặc biệt
.png)
1.2. Ý nghĩa hình học của tang và côtang
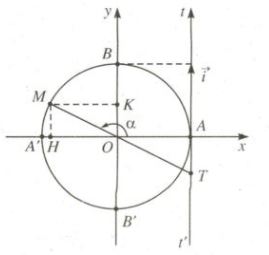
Ý nghĩa hình học của \(\tan \alpha \) và \(\cot \alpha\)
\(\tan \alpha = \overline {AT} \)
Trục t'At được gọi là trục tang.
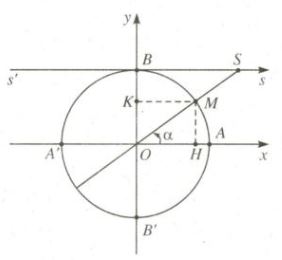
\(\cot \alpha = \overline {BS} \)
Trục s'Bs được gọi là trục côtang.
Chú ý:
\(\begin{array}{l}
\tan \left( {\alpha + k\pi } \right) = \tan \alpha \\
\cot \left( {\alpha + k\pi } \right) = \cot \alpha
\end{array}\)
1.3. Quan hệ giữa các giá trị lượng giác
1.3.1. Công thức lượng giác cơ bản
\(\begin{array}{l}
si{n^2}\alpha + co{s^2}\alpha = 1\\
1 + {\tan ^2}\alpha = \frac{1}{{co{s^2}\alpha }},\alpha \ne \frac{\pi }{2} + k\pi ,k \in Z\\
1 + co{t^2}\alpha = \frac{1}{{si{n^2}\alpha }},\alpha \ne k\pi ,k \in Z\\
\tan \alpha .\cot \alpha = 1,\alpha \ne \frac{{k\pi }}{2},k \in Z
\end{array}\)
1.3.2. Giá trị lượng giác của các cung có liên quan đặc biệt
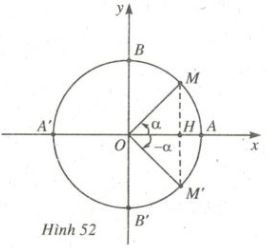
1) Cung đối nhau: \(\alpha \) và \( - \alpha \)
Các điểm cuối của hai cung AM và AM' đối xứng nhau qua trục hoành nên ta có:
\(\begin{array}{l}
\cos ( - \alpha ) = \,\cos \alpha \\
\sin ( - \alpha ) = \,\, - \sin \alpha \\
\tan ( - \alpha ) = - \tan \alpha \\
\cot ( - \alpha ) = - \cot \alpha
\end{array}\)
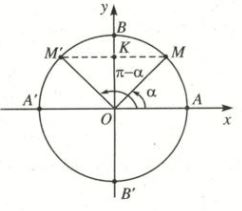
2) Cung bù nhau: \(\alpha \) và \(\pi - \alpha \)
Các điểm cuối của hai cung AM và AM' đối xứng với nhau qua trục tung, nên ta có:
\(\begin{array}{l}
\sin (\pi - \alpha ) = \,\,\,\,\,\,\sin \alpha \\
\cos (\pi - \alpha ) = - \cos \alpha \\
\tan (\pi - \alpha ) = - \tan \alpha \\
\cot (\pi - \alpha ) = - \cot \alpha
\end{array}\)
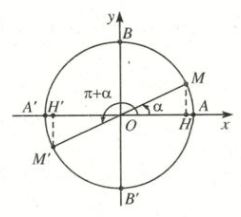
3) Hơn kém nhau \(\pi \): \(\pi \) và \(\left( {\alpha + \pi } \right)\)
Các điểm cuối của hai cung đối xứng nhau qua gốc tọa độ, nên ta có:
\(\begin{array}{l}
\sin (\alpha + \pi ) = - \sin \alpha \\
\cos (\alpha + \pi ) = - \cos \alpha \\
\tan (\alpha + \pi ) = \,\,\,\,\,\tan \alpha \\
\cot (\alpha + \pi ) = \,\,\,\,\,\cot \alpha
\end{array}\)
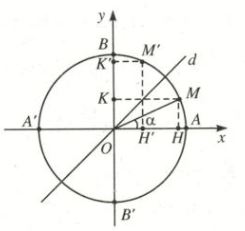
4) Cung phụ nhau: \(\alpha \) và \(\alpha - \frac{\pi }{2}\)
Các điểm cuối của hai cung đối xứng nhau qua đường phân giác d của góc xOy, nên ta có:
\(\begin{array}{l}
\sin \,\left( {\frac{\pi }{2} - \alpha } \right) = \cos \alpha \\
\cos \,\left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \\
\tan \,\left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \\
\cot \,\left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha
\end{array}\)
Chú ý: Để ghi nhớ các công thức trên dễ dàng ta học thuộc câu: “cos-đối, sin-bù, phụ-chéo, hơn kém nhau- tan và cot”.
2. Bài tập minh hoạ
Câu 1: Tính \(\sin \frac{{25\pi }}{4}\), \(cos\left( { - {{240}^o}} \right)\)
Hướng dẫn giải
Ta có \(\frac{{25\pi }}{4} = \frac{\pi }{4} + 3.2\pi \)
Suy ra \(\sin \frac{{25\pi }}{4} = \sin \frac{\pi }{4} = \frac{{\sqrt 2 }}{2}\)
Tương tự \( - {240^0} = {120^0} - {360^0}\)
Suy ra \(cos\left( { - {{240}^o}} \right) = cos{120^ \circ } = - \frac{1}{2}\)
Câu 2: Cho \(\sin \alpha = \frac{{\sqrt 3 }}{2}\) với \(0 < \alpha < \frac{\pi }{2}\). Tính \(\cos \alpha \)
Hướng dẫn giải
Ta có \(si{n^2}\alpha + co{s^2}\alpha = 1\)
\(\begin{array}{l}
\Rightarrow {\cos ^2}\alpha = 1 - {\sin ^2}\alpha \\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 1 - {\left( {\frac{{\sqrt 3 }}{2}} \right)^2} = \frac{1}{4}\\
\Rightarrow \cos \alpha = \pm \frac{1}{2}
\end{array}\)
Vì \(0 < \alpha < \frac{\pi }{2}\) nên \(\cos \alpha >0\) \( \Rightarrow \cos \alpha = \frac{1}{2}\)
Câu 3: Rút gọn biểu thức sau
\(A = \cos ({90^0} - x).\sin ({180^0} - x) - \sin ({90^0} - x).\cos ({180^0} - x)\)
Hướng dẫn giải
Sử dụng công thức cung phụ nhau và cung bù nhau
Ta có \(A = \cos ({90^0} - x).\sin ({180^0} - x) - \sin ({90^0} - x).\cos ({180^0} - x)\)
\(\begin{array}{l}
= \sin x.\sin x - \cos x.( - \cos x)\\
= {\sin ^2}x + {\cos ^2}x = 1
\end{array}\)
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho 0 < α < π/2. Xác định dấu của các giá trị lượng giác sau
a) \(\sin \left( {\alpha - \frac{\pi }{2}} \right)\)) b) \({\rm{cos}}\left( {\frac{\pi }{2} + \alpha } \right)\)
c) \({\rm{Cot}}\left( {\frac{{3\pi }}{2}{\rm{ }} - {\rm{ }}\alpha } \right)\) d) \({\rm{tan}}\left( {\alpha {\rm{ }} + {\rm{ }}\pi } \right)\)
Câu 2: Cho \({\rm{tan}}\alpha + {\rm{cot}}\alpha = m\), hãy tính theo m
a) \({\rm{tan}}2\alpha + {\rm{cot}}2\alpha \)
b) \({\rm{tan}}3\alpha + {\rm{cot}}3\alpha \)
3.2. Bài tập trắc nghiệm
Câu 1: Kết quả rút gọn của biểu thức \({\left( {\frac{{\sin \alpha + \tan \alpha }}{{{\rm{cos}}\alpha {\rm{ + 1}}}}} \right)^2} + 1\) bằng:
A. 2
B. 1+tan\(\alpha \)
C. \(\frac{1}{{{{\cos }^2}\alpha }}\)
D. \(\frac{1}{{{{\sin }^2}\alpha }}\)
Câu 2: Giá trị của \(M = {\cos ^2}{15^0} + {\cos ^2}{25^0} + {\cos ^2}{35^0} + {\cos ^2}{45^0} + {\cos ^2}{105^0} + {\cos ^2}{115^0} + {\cos ^2}{125^0}\) là:
A. M=4
B. M=\(\frac{7}{2}\)
C. M=\(\frac{1}{2}\)
D. \(M = 3 + \frac{{\sqrt 2 }}{2}.\)
Câu 3: Cho \({\rm{cos}}\alpha = - \frac{2}{5}\,\,\,\left( {\pi < \alpha < \frac{{2\pi }}{3}} \right)\). Khi đó \(\tan \alpha \) bằng:
A. \(\frac{{\sqrt {21} }}{5}\)
B. \(\frac{-{\sqrt {21} }}{2}\)
C. \(\frac{-{\sqrt {21} }}{5}\)
D. \(\frac{{\sqrt {21} }}{3}\)
Câu 4: Cho \(\sin a + \cos a = \frac{5}{4}\). Khi đó \(\sin a.\cos a\) có giá trị bằng:
A. 1
B. \(\frac{9}{32}\)
C. \(\frac{3}{16}\)
D. \(\frac{5}{4}\)
Câu 5: Nếu \(\cos x + \sin x = \frac{1}{2}\) và \({0^0} < x < {180^0}\) thì \(\tan x{\rm{ = }} - \frac{{p + \sqrt q }}{3}\) với cặp số nguyên (p, q) là:
A. (–4; 7)
B. (4; 7)
C. (8; 14)
D. (8; 7)
3.3. Trắc nghiệm Online
Các em hãy luyện tập bài trắc nghiệm Giá trị lượng giác của một cung Toán 10 sau để nắm rõ thêm kiến thức bài học.
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Tính được giá trị lượng giác của một cung.
- Nắm được phương pháp giải một số dạng toán cơ bản liên quan.
Tham khảo thêm
- doc Toán 10 Chương 6 Bài 1: Cung và góc lượng giác
- doc Toán 10 Chương 6 Bài 3: Công thức lượng giác
- doc Toán 10 Chương 6 Ôn tập chương 6 Cung Góc lượng giác và Công thức lượng giác