Giải bài tập SGK Vật lý 12 Bài 3: Con lắc đơn
Hướng dẫn Giải bài tập Vật lý 12 Bài 3 dưới đây sẽ giúp các em học sinh nắm vững phương pháp giải bài tập về con lắc đơn và ôn luyện tốt kiến thức. Mời các em cùng theo dõi.
Mục lục nội dung

Giải bài tập SGK Vật lý 12 Bài 3: Con lắc đơn
1. Giải bài 1 trang 17 SGK Vật lý 12
Thế nào là con lắc đơn? Khảo sát dao động của con lắc đơn về mặt động lực học. Chứng minh khi con lắc dao động nhỏ (sinα ≈ α) (rad), dao động của con lắc đơn là dao động điều hòa.
Phương pháp giải
- Để trả lời câu hỏi trên cần nắm được khái niệm và các đặc điểm của con lắc đơn.
- Phân tích các lực tác dụng lên vật, tìm giá trị thành phần lực →Pt và so sánh với lực kéo về của con lắc lò xo F = -kx.
Hướng dẫn giải
- Khái niệm con lắc đơn: Con lắc đơn gồm một vật nhỏ, khối lượng m, treo ở đầu một sợi dây không dãn, không đáng kể, chiều dài là l.
- Khảo sát dao động của con lắc đơn:
-
Vị trí cân bằng của con lắc là vị trí mà dây treo có phương thằng đứng.
-
Con lắc sẽ đứng yên mãi ở vị trí này nếu lúc đầu nó đứng yên. Kéo nhẹ quả cầu cho dây treo lệch khỏi vị trí cân bằng một góc rồi thả ra, ta thấy con lắc dao động quanh vị trí cân bằng trong mặt phẳng đứng đi qua điểm treo và vị trí ban đầu của vật.
- Xét con lắc đơn như hình vẽ:
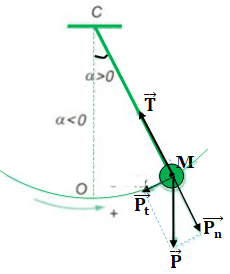
Dao động của con lắc đơn
Tại vị trí M, vật chịu tác dụng trọng lực →P và lực căng →T.
- →P được phân tích thành 2 thành phần: →Pn theo phương vuông góc với đường đi, →Pt theo phương tiếp tuyến với quỹ đạo.
- Lực căng →T và thành phần →Pn vuông góc với đường đi nên không làm thay đổi tốc độ của vật.
- Thành phần lực →Pt là lực kéo về có giá trị Pt = -mgsinα
- Nếu li độ góc α nhỏ thì sinα ≈ α (rad) thì Pt = -mgα = -mgsl so sánh với lực kéo về của con lắc lò xo F = -kx.
- Ta thấy mgl có vai trò của k → lg = mk
Vậy khi dao động nhỏ (sinα ≈ α (rad)), con lắc đơn dao động điều hòa.
2. Giải bài 2 trang 17 SGK Vật lý 12
Viết công thức tính chu kì của con lắc đơn khi dao động nhỏ.
Phương pháp giải
Để trả lời câu hỏi trên cần nắm được công thức tính chu kì T của con lắc đơn khi dao động nhỏ.
Hướng dẫn giải
Khi dao động nhỏ (sinα ≈ α (rad)), con lắc đơn dao động điều hòa với chu kì: T=2π√lg
3. Giải bài 3 trang 17 SGK Vật lí 12
Viết biểu thức của động năng, thế năng và cơ năng của con lắc đơn ở vị trí có góc lệch α bất kì.
Phương pháp giải
Để trả lời câu hỏi trên cần nắm được biểu thức của động năng, thế năng và cơ năng của con lắc đơn.
Hướng dẫn giải
-
Động năng của con lắc đơn: Wd=12mv2
-
Thế năng của con lắc đơn ở li độ góc α: Wt=mgl(1−cosα)
(mốc thế năng ở vị trí cân bằng)
-
Cơ năng của con lắc đơn được bảo toàn nếu bỏ qua mọi ma sát: W=12mv2+mgl(1−cosα) = const
- Vì cơ năng của con lắc đơn được bảo toàn nếu bỏ qua mọi ma sát, nên khi con lắc dao động, động năng tăng một lượng bao nhiêu thì thế năng giảm một lượng bấy nhiêu và ngược lại.
4. Giải bài 4 trang 17 SGK Vật lý 12
Hãy chọn đáp án đúng.
Chu kì của con lắc đơn dao động nhỏ (sinα ≈ α (rad)) là:
A. T=12π.√lg.
B. T=12π.√gl.
C. T=√2πlg.
D. T=2π√lg
Phương pháp giải
Để chọn phương án đúng ta cần nắm được công thức tính chu kì T của con lắc đơn dao động nhỏ.
Hướng dẫn giải
Công thức tính chu kì của con lắc đơn dao động: T=2π√lg
⇒ Đáp án: D
5. Giải bài 5 trang 17 SGK Vật lý 12
Hãy chọn câu đúng.
Một con lắc đơn dao động với biên độ góc nhỏ. Chu kì của con lắc không thay đổi khi:
A. Thay đổi chiều dai của con lắc.
B. Thay đổi gia tốc trọng trường.
C. Tăng biên độ góc đến 300.
D. Thay đổi khối lượng của con lắc.
Phương pháp giải
Để chọn phương án đúng ta cần nắm được công thức tính chu kì T của con lắc đơn khi dao động và hiểu được các thông số đại lượng trong công thức đó.
Hướng dẫn giải
Dựa vào công thức tính chu kì của con lắc đơn khi dao động là: T=2π√lg
Ta thấy chu kỳ của con lắc đơn chỉ phụ thuộc vào g và l mà không phụ thuộc vào khối lượng vật nặng m.
Vậy khi thay đổi khối lượng của con lắc thì chu kỳ của con lắc đơn không thay đổi.
⇒ Đáp án: D
6. Giải bài 6 trang 17 SGK Vật lý 12
Một con lắc đơn được thả không vận tốc đầu từ li độ góc α0. Khi con lắc qua vị trí cân bằng thì tốc độ của quả cầu con lắc là bao nhiêu?
A. √gl(1−cosα0)
B. √2glcosα0
C. √2gl(1−cosα0)
D. √glcosα0
Phương pháp giải
Để chọn phương án đúng ta cần nắm được đặc điểm của động năng, thế năng và cơ năng khi con lắc đi qua vị trí cân bằng ⇒ vmax.
Hướng dẫn giải
Khi con lắc qua vị trí cân bằng thì thế năng bằng 0, động năng cực đại (bằng cơ năng):
Ta có:
Wdmax=W12mv2max=mgl(1−cosα0)⇒vmax=±√2gl(1−cosα0)
⇒ Đáp án: C
7. Giải bài 7 trang 17 SGK Vật lý 12
Một con lắc đơn dài l = 2,00 m, dao động điều hòa tại một nơi có gia tốc rơi tự do g = 9,80 m/s2. Hỏi con lắc thực hiện được bao nhiêu dao động toàn phần trong 5,00 phút?
Phương pháp giải
Đây là dạng toán con lắc đơn dao động điều hòa và yêu cầu ta tính số dao động toàn phần mà con lắc thực hiện được trong thời gian cho trước.
Cách giải:
-
Bước 1: Tìm Chu kì dao động của con lắc đơn
-
Bước 2 : Tính số dao dộng đã thực hiện dựa trên công thức :
n=tT (dao động)
-
Bước 3: Thay số vào công thức và tính toán
Hướng dẫn giải
Tính tần số dao động của con lắc đơn:
T=2π√lg⇒f=1T=12π√gl=12π√9,82≈0,3523
Ta có tần số là số dao động vật thực hiện được trong
=> Số dao động toàn phần mà con lắc thực hiện được trong thời gian 5 phút = 300 s = 5.60 = 300 s là:
f.t = 0,3523.300 = 105,69 ≈106 dao động
Vậy, con lắc thực hiện được 106 dao động toàn phần trong 5 phút.
Tham khảo thêm
- doc Giải bài tập SGK Vật lý 12 Bài 1: Dao động điều hòa
- doc Giải bài tập SGK Vật lý 12 Bài 2: Con lắc lò xo
- doc Giải bài tập SGK Vật lý 12 Bài 4: Dao động tắt dần và dao động cưỡng bức
- doc Giải bài tập SGK Vật lý 12 Bài 5: Tổng hợp hai dao động điều hòa cùng phương, cùng tần số. Phương pháp Fre-nen
- doc Giải bài tập SGK Vật lý 12 Bài 6: TH: KS thực nghiệm các ĐL dao động của con lắc đơn




