Giải bài tập SGK Vật lý 12 Bài 14: Mạch có R, L, C nối tiếp

Phát biểu định luật Ôm đối với mạch điện xoay chiều có R, L, C mắc nối tiếp.

Phương pháp giải

Định luật Ôm đối với mạch điện xoay chiều: \(I = \frac{U}{Z}\)

Hướng dẫn giải

- Định luật Ôm của dòng điện xoay chiều của đoạn mạch R, L, C mắc nối tiếp: “Cường độ hiệu dụng trong mạch R, L, C mắc nối tiếp có giá trị bằng thương số của điện áp hiệu dụng giữa hai đầu mạch và tổng trở của mạch.”

- Biểu thức: \(I = \frac{U}{Z};Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \)

- Trong đó:

+ I là cường độ dòng điện hiệu dụng trong mạch (A)

+ U là điện áp hiệu dụng hai đầu mạch (V)

+ Z là tổng trở (Ω)

+ Z_L, Z_C là cảm kháng và dung kháng (Ω)

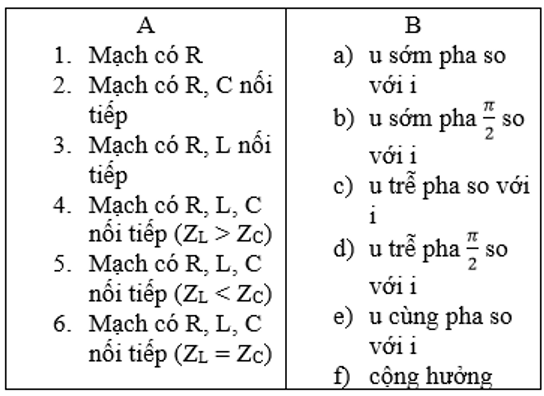
Dòng nào có cột A tương ứng với dòng nào ở cột B?

Phương pháp giải

Mạch điện xoay chiều được nói đến trong câu này bao gồm:

+ R, L, C nối tiếp

+ R, C nối tiếp

+ R, L nối tiếp

Hướng dẫn giải

Kết cột A tương ứng cột B.

1 – e), 2 – c), 3 – a), 4 – a), 5 – c), 6 – f)

Trong mạch điện xoay chiều nối tiếp, cộng hưởng là gì? Đặc trưng của cộng hưởng?

Phương pháp giải

Để trả lời câu hỏi này cần nắm vững định nghĩa và các đặc điểm của hiện tượng cộng hưởng.

Hướng dẫn giải

- Cộng hưởng điện là hiện tượng trong mạch R, L, C mắc nối tiếp có cường độ dòng điện trong mạch đạt giá trị cực đại khi cảm kháng và dung kháng có giá trị bằng nhau (Z_L = Z_C)

- Đặc điểm:

+ Tổng trở mạch Z = R là nhỏ nhất và I = U/R là lớn nhất.

+ Dòng điện i cùng pha với điện áp u

+ U = U_R

+ U_L = U_C

Mạch điện xoay chiều gồm có R = 20Ω mắc nối tiếp với tụ điện C = 1/2000π F. Tìm biểu thức cường độ tức thời i, biết u = 60√2cos100πt (V).

Phương pháp giải

- Áp dụng công thức định luật Ôm để tính I₀: I₀ = U₀/Z

- Tính tổng trở đối với mạch chỉ có L,R:

 \(Z = \sqrt {{R^2} + Z_C^2} \)

- Áp dụng công thức:  ZC= 1/ωC để tính dung kháng

- Áp dụng công thức sau:

 \(\tan \varphi = \frac{{{Z_C}}}{R};\varphi = {\varphi _u} - {\varphi _i}\) để tìm pha dao động của i

 ⇒ φ_i =π/4

Hướng dẫn giải

- Mạch R nối tiếp tụ điện thì i sớm pha so với u một góc φ.

- Biểu thức HĐT: 

u = 60√2cos100πt

- Biểu thức tổng quát: 

i = I₀cos(100πt + φi)

- Cường độ dòng điện: 

\({I_0} = \frac{{{U_0}}}{Z} = \frac{{{U_0}}}{{\sqrt {{R^2} + {{(\frac{1}{{C\omega }})}^2}} }} = \frac{{60\sqrt 2 }}{{\sqrt {{{20}^2} + {{(\frac{1}{{\frac{1}{{2000\pi }}.100\pi }})}^2}} }} = 3A\)

- Góc φ là:

  \(\tan \varphi = \frac{{ - {Z_C}}}{R} = \frac{{ - 20}}{{20}} = - 1 \Rightarrow \varphi = - \frac{\pi }{4}\)

- Góc φ_i là:

 \(\ \varphi = {\varphi _u} - {\varphi _i} \to {\varphi _i} = {\varphi _u} - \varphi = 0 - ( - \frac{\pi }{4}) = \frac{\pi }{4}\)

Vậy i = 3cos(100πt + π/4) (A)

Mạch điện xoay chiều gồm có R = 30Ω nối tiếp với cuộn cảm: L = 0,3/π H. Cho điện áp tức thời giữa hai đầu mạch u = 120√2cos100πt (V). Viết biểu thức của i.

Phương pháp giải

- Áp dụng công thức:  Z_L= ωL để tính  cảm kháng

- Áp dụng công thức định luật Ôm để tính I₀: I₀ = U₀/Z

- Tính tổng trở đối với mạch chỉ có L,R:

 \(Z = \sqrt {{R^2} + Z_L^2} \)

- Áp dụng công thức:

 \(\tan \varphi = \frac{{{Z_L}}}{R};\varphi = {\varphi _u} - {\varphi _i}\) để tìm pha dao động của i

⇒ φ_i = -π/4

Hướng dẫn giải

- Cảm kháng: Z_L = L.ω = 100π.(0,3/π) = 30Ω

- Mạch R nối tiếp với cuộn cảm thì i trễ pha so với u một góc φ

- Biểu thức HĐT:

u = 120√2cos100πt (V)

- Biểu thức tổng quát:

i = I₀cos(100πt + φi)

- Cường độ dòng điện:

 \({I_0} = \frac{{{U_0}}}{Z} = \frac{{{U_0}}}{{\sqrt {{R^2} + {{(\frac{1}{{C\omega }})}^2}} }} = \frac{{120\sqrt 2 }}{{\sqrt {{{30}^2} + {{30}^2}} }} = 4A\)

- Góc φ là:

 \(\tan \varphi = \frac{{{Z_L}}}{R} = \frac{{30}}{{30}} = 1 \Rightarrow \varphi = \frac{\pi }{4}\)

- Góc φ_i là:

  \(\varphi = {\varphi _u} - {\varphi _i} \to {\varphi _i} = {\varphi _u} - \varphi = 0 - \frac{\pi }{4} = - \frac{\pi }{4}\)

 Vậy i = 4cos(100πt – π/4) (A)

Mạch điện xoay chiều gồm điện trở R = 30Ω nối tiếp với một tụ điện C. Cho biết điện áp hiệu dụng giữa hai đầu mạch bằng 100V, giữa hai đầu tụ điện bằng 80V. Tính Z_C và cường độ hiệu dụng I.

Phương pháp giải

- Áp dụng công thức tính U cho mạch điện xoay chiều có 2 phần tử nối tiếp nhau:

\({U^2} = U_R^2 + U_C^2\) để tìm U_R

- Áp dụng công thức định luật Ôm để tính I và Z_C:

 \(I = \frac{{{U_R}}}{R};{Z_C} = \frac{{{U_C}}}{I}\)

Hướng dẫn giải

- Mạch R nối tiếp với C nên \(\overrightarrow {{U_R}} ,\overrightarrow {{U_C}} \) vuông góc với nhau.

- HĐT trên R là: 

\({U^2} = U_R^2 + U_C^2 \Rightarrow {U_R} = \sqrt {{U^2} - U_C^2} = \sqrt {{{100}^2} - {{80}^2}} = 60V\)

- Cường độ dòng điện:

 \( I = \frac{{{U_R}}}{R} = \frac{{60}}{{30}} = 2A \)

- Dung kháng là:

 \( {Z_C} = \frac{{{U_C}}}{I} = \frac{{80}}{2} = 40\Omega \)

Mạch điện xoay chiều gồm điện trở R = 40Ω ghép nối tiếp với cuộn cảm L. Cho biết điện áp tức thời hai đầu mạch u = 80cos100πt (V) và điện áp hiệu dụng hai đầu cuộn cảm U_L = 40V.

a) Xác định Z_L

b) Viết biểu thức của i.

Phương pháp giải

Giải câu a)

- Tính HĐT hiệu dụng: U = U₀/√2

- Tính U_R từ công thức đoạn mạch có hai phần tử:

 \({U^2} = U_R^2 + U_L^2\)

- Áp dụng công thức: : I = U_R/Z  để tính cường độ dòng điện

- Áp dụng công thức: Z_L = U_L/I để xác định dung kháng

Giải câu b)

- Áp dụng công thức: I₀ = I√2 để tính cường độ cục đại

-  Đoạn mạch R, L thì i trễ pha so với u một góc φ

⇒ φ_i = -π/4 

Hướng dẫn giải

- Mạch R nối tiếp với L:

+ u = 80cos100πt (V)

+  R = 40ω

+ U_L = 40V 

+ U = U₀/√2 = 40√2V

a) Xác định Z_L

- Vì u_L nhanh pha hơn cường độ dòng điện i một góc π/2, và u_R đồng pha với i nên \(\overrightarrow {{U_R}} ,\overrightarrow {{U_L}} \)   vuông góc với nhau.

- Hiệu điện thế:

 \({U^2} = U_R^2 + U_L^2 \Rightarrow {U_R} = \sqrt {{U^2} - U_L^2} = \sqrt {{{(40\sqrt 2 )}^2} - {{40}^2}} = 40V\)

- Cường độ dòng điện:

\( I = \frac{{{U_R}}}{R} = \frac{{40}}{{40}} = 1A \)

- Cảm kháng là:

 \( {Z_L} = \frac{{{U_L}}}{I} = \frac{{40}}{1} = 40\Omega \)

b) Biểu thức của i:

- Đoạn mạch R, L thì i trễ pha so với u một góc φ

- Biểu thức HĐT:

u = 80cos100πt (V)

- Biểu thức tổng quát:

i = I0cos(100πt + φi)

- Cường độ dòng điện:

I₀ = I√2 = √2 (A)

Vậy i = √2cos(100πt – π/4) (A)

Mạch điện xoay chiều gồm có: R = 30Ω, C = 1/5000π F, L = 0,2/π H. Biết hiệu áp tức thời hai đầu mạch u = 120√2cos100πt (V). Viết biểu thức của i.

Phương pháp giải

- Áp dụng công thức: Z_C= 1/ ωC, Z_L= Lω để tính dung kháng và cảm kháng.

- Tính tổng trở của mạch:

 \(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \)

- Áp dụng công thức: I₀ = U₀/Z  để tính I₀

- Áp dụng công thức:

 \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R};\varphi = {\varphi _u} - {\varphi _i}\)  để tìm pha dao động của i

⇒ φ_i = π/4

Hướng dẫn giải

- Dung kháng là:

 \({Z_C} = \frac{1}{{C\omega }} = \frac{1}{{\frac{1}{{5000\pi }}.100\pi }} = 50\Omega \)

- Cảm kháng là: 

Z_L = Lω = 20Ω

- Tổng trở:

 \(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} = 30\sqrt 2 \Omega \)

- Biểu thức của u: 

u = 120√2cos100πt (V)

- Biểu thức tổng quát:

  i = I₀cos(100πt + φ_i)

- Cường độ dòng điện:

 \({I_0} = \frac{{{U_0}}}{Z} = \frac{{120\sqrt 2 }}{{30\sqrt 2 }} = 4A\)

- Góc φ là:

 \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{20 - 50}}{{30}} = - 1 \Rightarrow \varphi = - \frac{\pi }{4}rad\)

- Góc φ_i là:

\( \varphi = {\varphi _u} - {\varphi _i} \to {\varphi _i} = {\varphi _u} - \varphi = 0 - ( - \frac{\pi }{4}) = \frac{\pi }{4}rad\)

Vậy i = 4cos(100πt + π/4) (A)

Mạch điện xoay chiều gồm có R = 40Ω, C = 1/4000π F , L = 0,1/π H. Biết hiệu áp tức thời hai đầu mạch u = 120√2cos100πt (V).

a) Viết biểu thức của i.

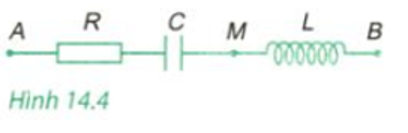
b) Tính U_AM (H.14.4)

Phương pháp giải

Giải câu a)

- Áp dụng công thức: Z_C= 1/ ωC, Z_L= ωL để tính dung kháng và cảm kháng

- Tính tổng trở của mạch:

 \(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \)

- Áp dụng công thức: I₀ = U₀/Z  để tính I₀

- Tìm pha của i so với u suy ra pha dao động của i bằng công thức sau: \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R};\varphi = {\varphi _u} - {\varphi _i}\)

Giải câu b)

 Áp dụng công thức:

 \(U = \sqrt {U_R^2 + U_C^2} \) để tính điện áp ở hai đầu AM

Hướng dẫn giải

a) Biểu thức của i:

- Điện trở là: R = 40Ω

- Dung kháng là:

  \( {Z_C} = \frac{1}{{C\omega }} = \frac{1}{{\frac{1}{{4000\pi }}.100\pi }} = 40\Omega \)

- Cảm kháng là:  Z_L = Lω = 10Ω

- Tổng trở:

 \(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} = \sqrt {{{40}^2} + {{(10 - 40)}^2}} = 50\Omega \)

- Biểu thức của u:

u = 120√2cos100πt (V)

- Biểu thức tổng quát: 

i = I₀cos(100πt + φ_i)

- Cường độ dòng điện: 

 \({I_0} = \frac{{{U_0}}}{Z} = \frac{{120\sqrt 2 }}{{50}} = 2,4\sqrt 2 A\)

- Góc φ là:

 \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{10 - 40}}{{40}} = - 0,75 \Rightarrow \varphi = - 0,6435rad\)

- Góc φ_i là:

 \(\varphi = {\varphi _u} - {\varphi _i} \to {\varphi _i} = {\varphi _u} - \varphi = 0 - ( - 0,6435) = 0,6435rad\)

Vậy i = 2,4√2cos(100πt + 0,6435) (A)

b) Điện áp hiệu dụng ở hai đầu AM:

 \({U_{AM}} = \sqrt {U_R^2 + U_C^2} = \sqrt {{{(I.R)}^2} + {{(I.{Z_C})}^2}} \)

⇒ \({U_{AM}} = \sqrt {{{(2,4.40)}^2} + {{(2,4.40)}^2}} = 96\sqrt 2 (V)\)

Cho mạch điện xoay chiều R = 20Ω, L = 0,2/π H và C = 1/2000π F. Biết điện áp tức thời hai đầu mạch u = 80cosωt (V), tính ω để trong mạch có cộng hưởng. Khi đó viết biểu thức i.

Phương pháp giải

- Cộng hưởng suy ra:

+ Tần số góc: \(\omega = \frac{1}{{\sqrt {LC} }}\) 

+ Pha của i: i cùng pha u

- Áp dụng công thức I₀=U₀/R để tính I₀

Hướng dẫn giải

- Mạch cộng hưởng thì: Z_L = Z_C 

⇒ ω²LC = 1

- Tần số góc:

 \( \omega = \frac{1}{{\sqrt {LC} }} = \frac{1}{{\sqrt {\frac{{0,2}}{\pi }.\frac{1}{{2000\pi }}} }} = 100\pi (rad/s)\)

- Pha của i: i cùng pha với u

- Biểu thức của u:

u = 80cosωt 

- Biểu thức tổng quát:

i = I₀cos(ωt)

- Cường độ dòng điện:

  \({I_0} = \frac{{{U_0}}}{R} = \frac{{80}}{{20}} = 4A\) 

Vậy:  i = 4cos(100πt) (A)

Chọn câu đúng.

Đoạn mạch có R, L, C mắc nối tiếp có R = 40Ω, 1/C.ω = 20Ω, ωL = 60Ω. Đặt vào hai đầu mạch điện áp u = 240√2cos100πt (V). Cường độ dòng điện tức thời trong mạch là:

A. i = 3√2cos100πt (A)                           B. 6cos(100πt + π/4) (A)

C. i = 3√2 cos(100πt – π/4) (A)              D. 6cos(100πt – π/4) (A)

Phương pháp giải

- Áp dụng công thức: Z_C= 1/ ωC để tính dung kháng

- Áp dụng công thức: Z_L= ωL để tính cảm kháng

- Tính tổng trở của mạch :

 \(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \)

- Áp dụng công thức: I₀ = U₀/Z  để tính I₀

- Áp dụng công thức:

 \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R};\varphi = {\varphi _u} - {\varphi _i}\) để tìm pha dao động của i

⇒ φ_i = -π/4

Hướng dẫn giải

- Điện trở là: R = 40Ω

- Cảm kháng là:  Z_L = 60Ω

- Dung kháng là: Z_C = 20Ω

- Tổng trở của mạch:

 \(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} = \sqrt {{{40}^2} + {{(60 - 20)}^2}} = 40\sqrt 2 \Omega \)

-  Biểu thức của u:

 u = 240√2cos100πt (V)

 - Biểu thức tổng quát:

i = I₀cos(100πt + φ_i)

- Cường độ dòng điện: 

\({I_0} = \frac{{{U_0}}}{Z} = \frac{{240\sqrt 2 }}{{40\sqrt 2 }} = 6A\)

- Góc φ là:

 \(\tan \varphi = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{60 - 20}}{{40}} = 1 \Rightarrow \varphi = \frac{\pi }{4}\)

- Góc φ_i là:

 \(\varphi = {\varphi _u} - {\varphi _i} \to {\varphi _i} = {\varphi _u} - \varphi = 0 - \frac{\pi }{4} = - \frac{\pi }{4}rad\)

Vậy i = 6cos(100πt – π/4) (A)

- Chọn đáp án D

Chọn đáp án đúng.

Đoạn mạch có R, L, C mắc nối tiếp có R = 40Ω, 1/C.ω = 30Ω, ωL = 30Ω. Đặt vào hai đầu mạch điện áp u = 120√2cos100πt (V). Cường độ dòng điện tức thời trong mạch là:

A. i = 3cos(100πt – π/2) (A)                   B. 3√2 (A)

C. i = 3cos(100πt) (A)                            D. 3√2cos(100πt ) (A)

Phương pháp giải

- Áp dụng công thức: Z_C= 1/ ωC để tính dung kháng

- Áp dụng công thức: Z_L=ω L  để tính cảm kháng

- Điều kiện cộng hưởng: Z_C = Z_L

- Áp dụng tính chất cộng hưởng để tìm pha của I so với u: i và u cùng pha

- Áp dụng định luật Ôm: : I₀=U₀/R để tính I₀

Hướng dẫn giải

- Dung kháng là: Z_C = 30Ω 

- Cảm kháng là:   Z_L = 30Ω 

- Vì Z_C =  Z_L nên mạch cộng hưởng 

⇒  i và u cùng pha

- Biểu thức của u:

u = 120√2cos100πt (V)

- Biểu thức tổng quát:

i = I₀cos100πt (A)

- Cường độ dòng điện:

 \({I_0} = \frac{{{U_0}}}{R} = \frac{{120\sqrt 2 }}{{40}} = 3\sqrt 2 A\)

Vậy i = 3√2cos100πt (A)

- Chọn đáp án D.