Giải bài tập SGK Toán 11 Chương 2 Bài 1: Quy tắc đếm

Từ các chữ số 1, 2, 3, 4 có thể lập được bao nhiêu số tự nhiên gồm:

a) Một chữ số?

b) Hai chữ số?

c) Hai chữ số khác nhau?

Phương pháp giải

a) Liệt kê và đếm.

b), c) Số tự nhiên cần lập có dạng \(\overline{ab}\), với \(a, b ∈ \left\{{1, 2, 3, 4}\right\}\).

+) Tìm số cách chọn cho chữ số a.

+) Tìm số cách chọn cho chữ số b.

+) Sử dụng quy tắc nhân.

Hướng dẫn giải

Câu a

Hiển nhiên từ các chữ số 1,2,3,4 ta có thể thành lập được 4 số tự nhiên có một chữ số, các số đó chính là các số 1,2,3,4.

Câu b

Gọi số có hai chữ số thoả mãn yêu cầu bài toán là: 

Với \(a,b\in \left \{ 1,2,3,4 \right \}\)

Có 4 cách chọn chữ số a.

Ứng với mỗi cách chọn chữ số a có 4 cách chọn chữ số b. Do vậy, theo quy tắc nhân ta có: 4.4=16 cách thành lập số .

Câu c

Gọi số có hai chữ số đó là , với a, b ∈ {1, 2, 3, 4} và a khác b.

Có bốn cách chọn chữ số a. Ứng với mỗi cách chọn chữ số a chỉ có 3 cách chọn chữ số b (vì \(a\neq b\))

Do đó, theo quy tắc nhân có 4.3 = 12 cách thành lập số  thoả mãn yêu cầu.

Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên bé hơn 100? Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên bé hơn 100?

Phương pháp giải

Số tự nhiên nhỏ hơn 100 là số tự nhiên có 1 hoặc 2 chữ số.

• Tìm số các số tự nhiên có 1 chữ số lập được từ các số 1; 2; 3; 4; 5; 6.
• Tìm số các số tự nhiên có 2 chữ số lập được từ các số 1; 2; 3; 4; 5; 6.
• Sử dụng quy tắc cộng.

Hướng dẫn giải

TH1: Có \(6\) số tự nhiên có 1 chữ số lập từ 1, 2, 3, 4, 5, 6.

TH2: Từ các chữ số \(1, 2, 3, 4, 5, 6\) lập số tự nhiên có hai chữ số.

Gọi số tự nhiên có hai chữ số là \(\overline {ab} \,\,\left( {a \ne 0} \right)\).

Có 6 cách chọn chữ số a.

Có 6 cách chọn chữ số b.

Áp dụng quy tắc nhân có \(6^2 = 36\) số tự nhiên có hai chữ số lập được từ các chữ số 1, 2, 3, 4, 5, 6.

Theo quy tắc cộng có \(6 + 36 = 42\) (số)

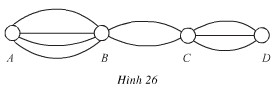
Các thành phố A, B, C, D được nối với nhau bởi các con đường như hình 26. Hỏi:

a) Có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần ?

b) Có bao nhiêu cách đi từ A đến D rồi quay lại A ?

Phương pháp giải

Sử dụng quy tắc cộng và quy tắc nhân phù hợp.

Hướng dẫn giải

Câu a

Để đi từ \(A\) đến \(D\) mà qua \(B\) và \(C\) chỉ một lần, phải thực hiện liên tiếp ba hành động sau đây:

Hành động 1: Đi từ \(A\) đến \(B\). Có \(4\) cách để thực hiện hành động này.

Hành động 2: Đi từ \(B\) đến \(C\). Có \(2\) cách để thực hiện hành động này.

Hành động 3: Đi từ \(C\) đến \(D\). Có \(3\) cách để thực hiện hành động này.

Theo quy tắc nhân suy ra số các cách để đi từ \(A\) đến \(D\) mà qua \(B\) và \(C\) chỉ một lần là \(4 . 2 . 3 = 24\) (cách).

Câu b

Khi đi từ A đến D rồi quay về A nghĩa là công việc được thực hiện qua 2 hành động:

Từ A đến D qua B, C chỉ 1 lần có 24 cách.

Từ D về A qua C, B chỉ 1 lần có 24 cách.

Áp dụng quy tắc nhân, số các cách để đi từ \(A\) đến \(D\) (mà qua \(B\) và \(C\) chỉ một lần), rồi quay lại \(A\) (mà qua \(C\) và \(B\) chỉ một lần) là:

\(24.24 = 576\) (cách).

Có ba kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và bốn kiểu dây (kim loại, da,, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?

Phương pháp giải

• Tìm số cách chọn mặt đồng hồ.
• Tìm số cách chọn dây.
• Sử dụng quy tắc nhân.

Hướng dẫn giải

Có 3 cách chọn mặt đồng hồ.

Có 4 bốn cách chọn dây.

Vậy theo quy tắc nhân có \(3 . 4 = 12\) cách để chọn một chiếc đồng hồ gồm một mặt và một dây.