Toán 12 Chương 2 Bài 3: Hàm số mũ Hàm số lôgarit
Các em học sinh đang tìm kiếm tài liệu tổng hợp kiến thức về hàm số mũ và hàm số lôgarit? Hãy tham khảo ngay bài giảng dưới đây của eLib biên soạn với những lý thuyết về các định nghĩa, tính chất và cách tìm đạo hàm của hàm số mũ, hàm số logarit, bên cạnh đó còn có các dạng bài tập toán cơ bản thường gặp. Sau đây mời các em cùng tham khảo.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Hàm số mũ
a) Định nghĩa hàm số mũ
Cho số thực dương \(a\) khác 1
Hàm số \(y=a^x\) được gọi là hàm số mũ cơ số \(a\).
b) Tính chất hàm số mũ
Tập xác định: \(\mathbb{R}.\)
Tập giá trị: \((0;+\infty )\)
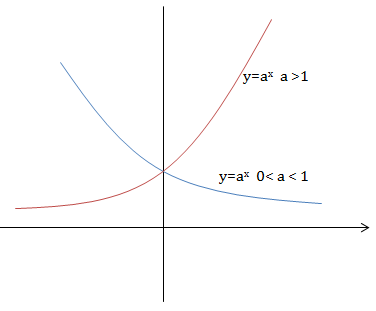
Với \(a>1\) hàm số \(y=a^x\) đồng biến trên \(\mathbb{R}.\)
Với \(0
Đồ thị hàm số mũ nhận trục \(Ox\) làm tiệm cận ngang.
c) Đạo hàm của hàm số mũ
Hàm số \(y=e^x\) có đạo hàm với mọi \(x\) và: \(\left ( e^x \right )'=e^x\)
Hàm số \(y=a^x(a>0,a\ne 1)\) có đạo hàm tại mọi \(x\) và: \(\left( {{a^x}} \right)' = {a^x}{\mathop{\rm lna}\nolimits}\)
Đối với hàm hợp
\(({e^u})' = u'.{e^u}\)
\(({a^u})' = {a^u}.\ln a.u'\)
1.2. Hàm số Lôgarit
a) Định nghĩa hàm số Lôgarit
Cho số thực dương \(a\) khác 1.
Hàm số \(y=\log_ax\) được gọi là hàm số lôgarit cơ số \(a.\)
b) Tính chất hàm số Lôgarit
Tập xác định: \(\left( {0; + \infty } \right).\)
Tập giá trị: \(\mathbb{R}.\)
Với \(a>1\): \(y=\log_ax\) là hàm số đồng biến trên \(\left( {0; + \infty } \right).\)
Với \(0
Với \(x_1>0,x_2>0\): \(\log_ax_1=\log_ax_2\Leftrightarrow x_1=x_2\)
c) Đạo hàm của hàm số logarit
\(\left( {{{\log }_a}x} \right)' = \frac{1}{{x\ln a}}\)
\(\left( {{{\log }_a}\left| x \right|} \right)' = \frac{1}{{x\ln a}}\)
\(\left( {\ln x} \right)' = \frac{1}{x}\)
Đối với hàm hợp
\(\left( {{{\log }_a}u} \right)' = \frac{{u'}}{{u.\ln a}}\)
\(\left( {\ln u} \right)' = \frac{{u'}}{{\ln u}}\)
1.3. Chú ý
- Nếu \(a > 1\) thì \(\ln a > 0\), suy ra (ax)’ > 0,∀x và (logax)’ > 0, ∀x > 0;
do đó hàm số mũ và hàm số lôgarit với cơ số lớn hơn 1 đều là những hàm số luôn luôn đồng biến.
Tương tự, nếu \(0 < a< 1\) thì \(\ln a < 0\), (ax)’ < 0 và (logax)’ < 0, ∀x > 0; hàm số mũ và hàm số lôgarit với cơ số nhỏ hơn 1 đều là những hàm số luôn luôn nghịch biến.
- Công thức đạo hàm của hàm số lôgarit có thể mở rộng thành
\( (\ln |x|)'= \dfrac{1}{x}, ∀x \ne 0\) và (loga|x|)’ = \(\dfrac{1}{x \ln a}\), ∀x\(\ne\) 0.
2. Bài tập minh họa
2.1. Bài tập 1
Tìm tập xác định của các hàm số sau:
a) \(y = {\log _2}(25 - 4{x^2})\)
b) \(y = {\log _{2x + 1}}(3x + 1) - 2{\log _{3x + 1}}(2x + 1)\)
c) \(y = {\log _{\sqrt {3x + 2} }}(1 - \sqrt {1 - 4{x^2}} )\)
Hướng dẫn giải
a) Điều kiện: \(25 - 4{x^2} > 0 \Leftrightarrow - \frac{5}{2} < x < \frac{5}{2}\)
Vậy tập xác định của hàm số là: \(D = \left( { - \frac{5}{2};\frac{5}{2}} \right).\)
b) Điều kiện: \(\left\{ \begin{array}{l} 0 < 2x + 1 \ne 1\\ 0 < 3x + 1 \ne 1 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x \ge - \frac{1}{3}\\ x \ne 0 \end{array} \right.\)
Vậy tập xác định của hàm số là: \(D = \left[ { - \frac{1}{3}; + \infty } \right)\backslash \left\{ 0 \right\}\).
c) Điều kiện: \(\left\{ \begin{array}{l} 0 < 3x + 2 \ne 1\\ 1 - \sqrt {1 - 4{x^2}} > 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} x > - \frac{2}{3}\\ x \ne - \frac{1}{3}\\ x \ne 0 \end{array} \right.\)
Vậy tập xác định của hàm số là: \(D = \left( { - \frac{2}{3}; + \infty } \right)\backslash \left\{ { - \frac{1}{3};0} \right\}\).
2.2. Bài tập 2
Tính đạo hàm các hàm số sau:
a) \(y = \left( {{x^2} - 2x + 2} \right){e^x}\)
b) \(y = {2^{{x^2} - 3x}}\)
c) \(y = \frac{{{2^x} - 1}}{{{5^x}}}\)
d) \(y = \frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}}\)
Hướng dẫn giải
a) \(y = \left( {{x^2} - 2x + 2} \right){e^x} \Rightarrow y' = \left( {2x - 2} \right){e^x} + \left( {{x^2} - 2x + 2} \right){e^x} = \left( {{x^2}} \right){e^x}\)
b) \(y = {2^{{x^2} - 3x}} \Rightarrow y' = (2x - 3){.2^{{x^2} - 3x}}.\ln 2\)
c) \(y = \frac{{{2^x} - 1}}{{{5^x}}} = {\left( {\frac{2}{5}} \right)^x} - {\left( {\frac{1}{5}} \right)^x} \Rightarrow y' = {\left( {\frac{2}{5}} \right)^x}.\ln \frac{2}{5} - {\left( {\frac{1}{5}} \right)^x}.\ln \frac{1}{5}\)
d) \(y = \frac{{{e^x} - {e^{ - x}}}}{{{e^x} + {e^{ - x}}}}\)
\(\Rightarrow y' = \frac{{\left( {{e^x} + {e^{ - x}}} \right)\left( {{e^x} + {e^{ - x}}} \right) - \left( {{e^x} - {e^{ - x}}} \right)\left( {{e^x} - {e^{ - x}}} \right)}}{{{{\left( {{e^x} + {e^{ - x}}} \right)}^2}}} = \frac{4}{{{{\left( {{e^x} + {e^{ - x}}} \right)}^2}}}\)
2.3. Bài tập 3
Tính đạo hàm các hàm số sau:
a) \(y = \ln \left( {{x^2} + 1} \right)\)
b) \(y = \frac{{\ln x}}{x}\)
c) \(y = \left( {1 + \ln x} \right)\ln x\)
d) \(y = {\log _3}(3{x^2} + 2x + 1)\)
Hướng dẫn giải
a) \(y = \ln \left( {{x^2} + 1} \right) \Rightarrow y' = \frac{{2x}}{{{x^2} + 1}}\)
b) \(y = \frac{{\ln x}}{x} \Rightarrow y' = \frac{1}{{{x^2}}}\left( {\frac{1}{x}.x - \ln x} \right) = \frac{{1 - \ln x}}{{{x^2}}}\)
c) \(y = \left( {1 + \ln x} \right)\ln x \Rightarrow y' = \frac{{\ln x}}{x} + \frac{{1 + \ln x}}{x} = \frac{{1 + 2\ln x}}{x}\)
d) \(y = {\log _3}(3{x^2} + 2x + 1)\) \(\Rightarrow y' = \frac{{\left( {3{x^2} + 1x + 1} \right)'}}{{(3{x^2} + 2x + 1).\ln 3}} = \frac{{6x + 2}}{{(3{x^2} + 2x + 1).\ln 3}}\)
2.4. Bài tập 4
Tìm m để hàm số \(y={\log _2}(2{x^2} + 3x + 2m - 1)\) xác định \(\forall x \in \mathbb{R}\).
Hướng dẫn giải
Điều kiện: \(2{x^2} + 3x + 2m - 1 > 0,\forall x \in \mathbb{R}\)
Ta có: \(\Delta = {3^2} - 4.2.(2m - 1) = 17 - 16m > 0 \Leftrightarrow m < \frac{{17}}{{16}}.\)
Vậy với \(m<\frac{17}{16}\) hàm số xác định \(\forall x \in \mathbb{R}\).
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Tính đạo hàm của các hàm số:
a) \(y=2x{{e}^{x}}+3\sin 2x\)
b) \(y=5{{x}^{2}}-{{2}^{x}}\cos x\)
c) \(y=\dfrac{x+1}{{{3}^{x}}}\)
Câu 2: Tìm tập xác định của các hàm số:
a) \(y={{\log }_{2}}\left( 5-2x \right)\)
b) \(y={{\log }_{3}}\left( {{x}^{2}}-2x \right)\)
c) \(y=lo{{g}_{\frac{1}{5}}}\left( {{x}^{2}}-4x+3 \right)\)
d) \(y={{\log }_{0,4}}\dfrac{3x+2}{1-x}\)
Câu 3: Tìm tọa độ giao điểm của đồ thị của mỗi cặp hàm số sau
a) \(y=2^x\) và \(y=8\)
b) \(y=3^x\) và \(y=\dfrac 1 3\)
c) \(y={{\left( \dfrac{1}{4} \right)}^{x}} \) và \(y=\dfrac 1 {16}\)
Câu 4: Từ đồ thị hàm số \(y=3^x\), hãy vẽ đồ thị các hàm số sau:
a) \(y=3^x-2\)
b) \( y=3^x+2\)
c) \(y=|3^x-2| \)
d) \(y=2-3^x\)
Câu 5: Vẽ đồ thị của các hàm số:
a) \(y=\log x\)
b) \(y={{\log }_{\frac{1}{2}}}x\)
3.2. Bài tập trắc nghiệm
Câu 1: Kết quả tính đạo hàm nào sau đây sai?
A. \({\left( {{{\log }_3}x} \right)'} = \frac{1}{{x\ln 3}}\)
B. \({\left( {{2^x}} \right)'} = {2^x}\ln 2\)
C. \({\left( {\ln x} \right)'} = \frac{1}{x}\)
D. \({\left( {{e^{5x}}} \right)'} = {e^{5x}}\)
Câu 2: Tính đạo hàm của hàm số \(y = \ln \frac{{x - 1}}{{x + 2}}.\)
A. \(y' = \frac{{ - 3}}{{\left( {x - 1} \right)\left( {x + 2} \right)}}\)
B. \(y' = \frac{3}{{\left( {x - 1} \right){{\left( {x + 2} \right)}^2}}}\)
C. \(y' = \frac{3}{{\left( {x - 1} \right)\left( {x + 2} \right)}}\)
D. \(y' = \frac{{ - 3}}{{\left( {x - 1} \right){{\left( {x + 2} \right)}^2}}}\)
Câu 3: Cho các hàm số \(y = {\log _2}x;y = {\left( {\frac{e}{\pi }} \right)^x};\) \(y = \log {\rm{x}};y = {\left( {\frac{{\sqrt 3 }}{2}} \right)^x}.\)
Trong các hàm số trên, có bao nhiêu hàm số nghịch biến trên tập xác định của nó?
A. 2
B. 3
C. 1
D. 4
Câu 4: Tìm tập xác định \(D\) của hàm số \(y = {\log _3}\left( {{x^2} + 3x + 2} \right)\).
A. \(D = \left[ { - 2, - 1} \right].\)
B. \(D = \left( { - \infty , - 2} \right) \cup \left( { - 1, + \infty } \right)\).
C. \(D = \left( { - 2, - 1} \right)\).
D. \(D = \left( { - \infty , - 2} \right] \cup \left[ { - 1, + \infty } \right)\).
3.3. Trắc nghiệm Online
Các em hãy luyện tập bài trắc nghiệm Hàm số mũ Hàm số lôgarit Toán 12 sau để nắm rõ thêm kiến thức bài học.
4. Kết luận
Qua bài học này giúp các em học sinh nắm được một số nội dung chính như sau:
- Biết vận dụng tính chất các hàm mũ, hàm lôgarit vào việc so sánh hai số, hai biểu thức chứa mũ, hàm số lôgarit.
- Biết vẽ đồ thị các hàm số lũy thừa, hàm số mũ và hàm số lôgarit.
- Tính được đạo hàm các hàm số y = ex, y = lnx
Tham khảo thêm
- doc Toán 12 Chương 2 Bài 1: Lũy thừa
- doc Toán 12 Chương 2 Bài 2: Hàm số lũy thừa
- doc Toán 12 Chương 2 Bài 3: Lôgarit
- doc Toán 12 Chương 2 Bài 5: Phương trình mũ và phương trình lôgarit
- doc Toán 12 Chương 2 Bài 6: Bất phương trình mũ và bất phương trình lôgarit
- doc Toán 12 Ôn tập chương 2: Hàm số lũy thừa, Hàm số mũ và Hàm số Lôgarit



