Toán 12 Chương 2 Bài 2: Hàm số lũy thừa

Hàm số luỹ thừa là hàm số có dạng \(y=x^{\alpha}\), trong đó \(\alpha\) là một hằng số tuỳ ý.
Từ định nghĩa các luỹ thừa, ta thấy: 

• Hàm số \(y=x^n\) với n nguyên dương, xác định với mọi \(x \in \mathbb{R}\).
• Hàm số \(y=x^n\), với n nguyên âm hoặc n = 0, xác định với mọi \(x \in \mathbb{R}\backslash \left\{ 0 \right\}\).
• Hàm số \(y=x^{\alpha}\), với \(\alpha\) không nguyên, có tập xác định là tập hợp các số thực dương \(\left( {0; + \infty } \right)\)

Người ta chứng minh được rằng hàm số lũy thừa liên tục trên tập xác định của nó.

Chú ý
Theo định nghĩa, đẳng thức \(\sqrt[n]{x} = {x^{\frac{1}{n}}}\) chỉ xảy ra nếu \(x>0\) do đó, hàm số \(y=x^\frac{1}{n}\) không đồng nhất với hàm số \(y = \sqrt[n]{x}(n \in {\mathbb{N}^*})\). Chẳng hạn, hàm số \(y = \sqrt[3]{x}\) là hàm số căn bậc ba, xác định với mọi \(x \in \mathbb{R}\); còn hàm số luỹ thừa \(y=x^\frac{1}{3}\) chỉ xác định trên \(\left( {0; + \infty } \right)\).

a) Đạo hàm của hàm số lũy thừa với số mũ tổng quát 

- Hàm số \(y = {x^\alpha }\) có đạo hàm tai mọi \(x ∈ (0; +∞)\) và \(y' = \left( {{x^\alpha }} \right)' = \alpha {x^{\alpha  - 1}}\)

- Nếu hàm số \(u=u(x)\) nhận giá trị dương và có đạo hàm trong khoảng \(J\) thì hàm số \(y = {u^\alpha }\left( x \right)\) cũng có đạo hàm trên \(J\) và \[y' = \left[ {{u^\alpha }\left( x \right)} \right]' = \alpha {u^{\alpha  - 1}}\left( x \right)u'\left( x \right)\]

b) Đạo hàm của hàm số lũy thừa với số mũ nguyên dương

Trong trường hợp số mũ nguyên dương, hàm số lũy thừa \(y=x^n\) có tập xác định là \(R\) và có đạo hàm trên toàn trục số. Công thức tính đạo hàm số lũy thừa tổng quát được mở rộng thành \(\forall x \in R,\left( {{x^n}} \right)' = n{x^{n - 1}}\) và \[\forall x \in J,\left[ {{u^n}\left( x \right)} \right]' = n{u^{n - 1}}\left( x \right)u'\left( x \right)\] nếu \(u= u(x) \) có đạo hàm trong khoảng \(J\).

c) Đạo hàm của hàm số  lũy thừa với số mũ nguyên âm

Nếu số mũ là số nguyên âm thì hàm số lũy thừa \(y=x^n\) có tập xác định là \(R\backslash \left\{ 0 \right\}\) và có đạo hàm tại mọi \(x\) khác \(0\), công thức đạo hàm hàm số lũy thừa tổng quát được mở rộng thành \(\forall x \ne 0,\left( {{x^n}} \right)' = n{x^{n - 1}}\) và \[\forall x \in J,\left[ {{u^n}\left( x \right)} \right]' = n{u^{n - 1}}\left( x \right)u'\left( x \right)\]

Nếu \(u= u(x) \ne 0\) có đạo hàm trong khoảng \(J\).

5. Đạo hàm của căn thức

Hàm số \(y = \sqrt[n]{x}\) có thể xem là mở rộng của hàm lũy thừa \(y = {x^{\frac{1}{n}}}\) (tập xác định của \(y = \sqrt[n]{x}\) chứa tập xác định của \(y = {x^{\frac{1}{n}}}\) và trên tập xác định của \(y = {x^{\frac{1}{n}}}\) thì hai hàm số trùng nhau).

Khi \(n\) lẻ thì hàm số \(y = \sqrt[n]{x}\) có tập xác định \(R\). Trên khoảng \((0; +∞) \) ta có \(y = \sqrt[n]{x} = {x^{\frac{1}{n}}}\) và \(\left( {{x^{\frac{1}{n}}}} \right)' = \dfrac{1}{n}{x^{\frac{1}{n} - 1}}\), do đó \(\left( {\sqrt[n]{x}} \right)' = \dfrac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}}\).

Công thức này còn đúng cả với \(x < 0\) và hàm số \(y = \sqrt[n]{x}\) không có đạo hàm tại \(x= 0\).

Khi \(n\) chẵn hàm \(y = \sqrt[n]{x}\) có tập xác định là \([0;+∞)\), không có đạo hàm tại \(x= 0\) và có đạo hàm tại mọi \(x > 0\) tính theo công thức:

\[ \left( {\sqrt[n]{x}} \right)' =\left( {\sqrt[n]{x}} \right)' = \dfrac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}}\]

Tóm lại, ta có \( \left( {\sqrt[n]{x}} \right)' =\left( {\sqrt[n]{x}} \right)' = \dfrac{1}{{n\sqrt[n]{{{x^{n - 1}}}}}}\) đúng với mọi \(x\) làm cho hai vế có nghĩa.

Sử dụng quy tắc đạo hàm hàm hợp ta suy ra: Nếu \(u=u(x)\) là hàm có đạo hàm trên khoảng \(J\) và thỏa mãn điều kiện \(u(x) > 0, ∀x ∈ J\) khi \(n\) chẵn, \(u\left( x \right) \ne 0,\forall x \in J\) khi \(n\) lẻ thì

\[\forall x \in J,\left( {\sqrt[n]{{u\left( x \right)}}} \right)' = \dfrac{{u'\left( x \right)}}{{n\sqrt[n]{{{u^{n - 1}}\left( x \right)}}}}\]

Tập xác định của hàm số lũy thừa luôn chứa khoảng \(\left( {0; + \infty } \right)\) với mọi \(\alpha \in \mathbb{R}\). 

Hình dạng của đồ thị hàm số lũy thừa trong các trường hợp xét trên tập \(\left( {0; + \infty } \right)\):

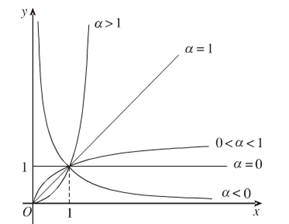
Chú ý

Khi khảo sát hàm số \(y = {x^\alpha }\) với \(\alpha \) cụ thể, cần xét hàm số trên toàn tập xác định của nó (chứ không phải chỉ xét trên khoảng \((0; +∞)\) như trên).

Tìm tập xác định của các hàm số sau:

a) \(y= \left ( 1-x \right )^{\frac{-1}{3}}\)

b) y= \(\left ( 2-x^{2} \right )^{\frac{3}{5}}\)

c) \(y= \left ( x^{2}-1 \right )^{-2}\)

Hướng dẫn giải

a) \(y= \left ( 1-x \right )^{\frac{-1}{3}}\) có \(n =  - \dfrac{1}{3} \notin Z\) xác định khi và chỉ khi:

\(1-x > 0 ⇔ x< 1\). 

Vậy \(D=(-∞; 1)\).

b) \(y= \left ( 2-x^{2} \right )^{\frac{3}{5}}\) có \(n = \dfrac{3}{5} \notin Z\) xác định khi và chỉ khi:

\(2-x^2> 0  \Leftrightarrow {x^2} < 2\)

\(⇔ -\sqrt{2} < x <\) \(\sqrt{2}\).

Vậy \(D= \left( {-\sqrt{2}}; {\sqrt{2}}\right)\).

c) \(y= \left ( x^{2}-1 \right )^{-2}\) có \(n =  - 2 \in {Z^ - }\) xác định khi và chỉ khi:

\(x^2-1\ne 0 ⇔ x \ne ± 1\).

Vậy \(D=\mathbb R {\rm{\backslash }} {\rm{\{  - 1;1\} }}\) .

Tính đạo hàm các hàm số

a) \(y = {x^{{{ - 2} \over 3}}};\,\,y = {x^\pi };\,\,y = {x^{\sqrt 2 }}\)

b) \(y = {(3{x^2} - 1)^{( - \sqrt 2 )}}\)

Hướng dẫn giải

a) 

\(\eqalign{
& y' = ({x^{{{ - 2} \over 3}}})' = - {2 \over 3}.{x^{({{ - 2} \over 3} - 1)}} \cr &= {{ - 2} \over 3}.{x^{{{ - 5} \over 3}}} \cr
& y' = ({x^\pi })' = \pi .{x^{\pi - 1}} \cr
& y' = ({x^{\sqrt 2 }})' = \sqrt 2 .{x^{\sqrt 2 - 1}} \cr} \)

b) 

\(\eqalign{
& y' = \left[ {{{(3{x^2} - 1)}^{( - \sqrt 2 )}}} \right]' \cr
& = - \sqrt 2 {(3{x^2} - 1)^{( - \sqrt 2 - 1)}}.(3{x^2} - 1)' \cr
& = - \sqrt 2 {(3{x^2} - 1)^{( - \sqrt 2 - 1)}}.6x \cr
& = - 6 \sqrt 2 x{(3{x^2} - 1)^{( - \sqrt 2 - 1)}} \cr} \)

Tính đạo hàm các hàm số sau

a) \(y = {(2x + 1)^\pi }\)

b) \(y = {(3{x^2} - 1)^{ - \sqrt 2 }}\)

c) \(y = {\left( {2{x^2} + x - 1} \right)^{\frac{2}{3}}}\)

Hướng dẫn giải

a) \(y' = \pi {(2x + 1)^{\pi - 1}}(2x + 1)' = 2\pi {(2x + 1)^{\pi - 1}}.\)

b) \(y' = - \sqrt 2 {\left( {3{x^2} - 1} \right)^{ - \sqrt 2 - 1}}(3{x^2} - 1)' = - 6\sqrt 2 x{(3{x^2} - 1)^{ - \sqrt 2 - 1}}.\)

c) \(y' = \frac{2}{3}{(2{x^2} + x - 1)^{ - \frac{1}{3}}}(4x + 1).\)

Câu 1: Tìm tập xác định của các hàm số:

a) \(y={{\left( 1-x \right)}^{-\dfrac{1}{3}}}\) 

b) \(y={{\left( 2-{{x}^{2}} \right)}^{\dfrac{3}{5}}}\)

c) \(y={{\left( {{x}^{2}}-1 \right)}^{-2}}\) 

d) \(y={{\left( {{x}^{2}}-x-2 \right)}^{\sqrt{2}}}\).

Câu 2: Tính đạo hàm của các hàm số:

a) \(y={{\left( 2{{x}^{2}}-x+1 \right)}^{\frac{1}{3}}}\) 

b) \(y={{\left( 4-x-{{x}^{2}} \right)}^{\frac{1}{4}}}\)

c) \(y={{\left( 3x+1 \right)}^{\frac{\pi }{2}}}\)

d) \(y={{\left( 5-x \right)}^{\sqrt{3}}}\)

Câu 3: Tính đạo hàm của các hàm số

a) \(y=(x^2-4x+3)^{-2}\)

b) \(y=(x^3-8)^{\frac{\pi} 3}\)

c) \(y=(x^3-3x^2+2x)^{\frac 1 4}\)

d) \(y=(x^2+x-6)^{-\frac 1 3}\)

Câu 4: Khảo sát sự biến thiên và vẽ đồ thị của các hàm số:

a) \(y={{x}^{\frac{4}{3}}}\)

b) \(y={{x}^{-3}} \)

Câu 5: Vẽ đồ thị của các hàm số \(y=x^2\) và \(y=x^{\frac 1 2}\) trên cùng một hệ trục tọa độ. Hãy so sánh giá trị của các hàm số đó khi \(x=0,5;1;\dfrac 3 2; 2; 3; 4\)

Câu 1: Tính đạo hàm của hàm số  \(y = \sqrt[3]{{{x^2}.\sqrt {{x^3}} }}.\)

A. \(y' = \sqrt[9]{x}\)

B. \(y' = \frac{7}{6}\sqrt[6]{x}\)

C. \(y' = \frac{4}{3}\sqrt[3]{x}\)

D. \(y' = \frac{6}{{7\sqrt[7]{x}}}\)

Câu 2: Tập xác định của hàm số \(y = {\left( {1 - 2x} \right)^{\frac{1}{3}}}\) là:

A. \(\left( { - \infty ;\frac{1}{2}} \right)\) 

B.  \(\left( {0; + \infty } \right)\) 

C. \(\mathbb{R}\)

D. \(\left( { - \infty ;\frac{1}{2}} \right]\)

Câu 3: Cho hàm số \(y = {x^{\frac{1}{4}}}\left( {10 - x} \right),x > 0\)

Khẳng định nào sau đây là đúng?

A.  Hàm số ngịch biến trên (0;2).

B.  Hàm số ngịch biến trên khoảng (5; +∞) .

C. Hàm số đồng biến trên (2; +∞) .

D. Hàm số không có điểm cực trị nào.

Câu 4: Số nào lớn nhất trong các số được liệt kê trong bốn phương án A,B,C,D dưới đây?

A. \(\sqrt {3\sqrt 5 } \)

B. \(\sqrt {2\sqrt {11} } \)

C. \(\sqrt {4\sqrt 3 } \)

D. \(\sqrt {5\sqrt 2 } \)

Câu 5: Tính đạo hàm của hàm số  \(y = {2^{\ln x + {x^2}}}.\)

A. \(y' = \left( {\frac{1}{x} + 2x} \right){2^{\ln x + {x^2}}}\)

B. \(y' = \left( {\frac{1}{x} + 2x} \right){2^{\ln x + {x^2}}}.\ln 2\)

C. \(y' = \frac{{{2^{\ln x + {x^2}}}}}{{\ln 2}}\)

D. \(y' = \left( {\frac{1}{x} + 2x} \right)\frac{{{2^{\ln x + {x^2}}}}}{{\ln 2}}\)

Qua bài học này, các em cần nắm được 1 số nội dung chính quan trọng như sau:

• Biết định nghĩa lũy thừa với số mũ nguyên, căn bậc n, luỹ thữ với số mũ hữu tỉ, vô tỉ
• Biết cách vận dụng các tính chất của luỹ thừa với số mũ thực để giải toán