Toán 12 Chương 1 Bài 1: Sự đồng biến, nghịch biến của hàm số

• Hàm số y = f(x) đồng biến (tăng) trên K ⇔ ∀x₁, x₂ ∈ K, x₁ < x₂ thì f(x₁) < f(x₂).
• Hàm số y = f(x) nghịch biến (giảm) trên K ⇔ ∀x₁, x₂ ∈ K, x₁ < x₂ thì f(x₁) > f(x₂).

Cho hàm số f có đạo hàm trên K

• Nếu f đồng biến trên K thì f'(x) ≥ 0 với mọi x ∈ K.
• Nếu f nghịch biến trên K thì f'(x) ≤ 0 với mọi x ∈ K.

Cho hàm số f có đạo hàm trên K

• Nếu f'(x) ≥ 0 với mọi x ∈ K và f'(x) = 0 chỉ tại một số hữu hạn điểm thuộc k thì f đồng biến trên K.
• Nếu f'(x) ≤ 0 với mọi x ∈ K và f'(x) = 0 chỉ tại một số hữu hạn điểm thuộc K thì f nghịch biến trên K.
• Nếu f'(x) = 0 với mọi x ∈ K thì f là hàm hằng trên K.

• Bước 1: Tìm tập xác định
• Bước 2: Tính đạo hàm f'(x). Tìm các điểm xi (i= 1 , 2 ,..., n) mà tại đó đạo hàm bằng 0  hoặc không xác định.
• Bước 3: Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
• Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

Tìm khoảng đơn điệu của các hàm số sau: \(y = {x^3} - 3{x^2} + 3x + 7\)

Hướng dẫn giải

Xét hàm số: \(y = {x^3} - 3{x^2} + 3x + 7\)

TXĐ: \(D = R\)

\(y' = 3{x^2} - 6x + 3\)

\(y' = 0 \Leftrightarrow 3{x^2} - 6x + 3 = 0 \Leftrightarrow x = 1\)

Bảng biến thiên

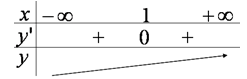
Kết luận: Hàm số đồng biến trên \(R\)

Tìm tất cả các giá trị thực của tham số m để hàm số \(y = {x^3} + 3{x^2} + mx + m\) đồng biến trên \(R\)

Hướng dẫn giải

Xét hàm số \(y = {x^3} + 3{x^2} + mx + m\)

TXĐ: \(D = R\)

\(y' = 3{x^2} + 6x + m\)

Hàm số đồng biến trên \(R\) khi \(y' \ge 0,\forall x \in R \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\Delta ' \le 0}\\
{a = 1 > 0}
\end{array}} \right. \Leftrightarrow 9 - 3m < 0 \Leftrightarrow m \ge 3\)

Kết luận: với \(m \ge 3\) thì hàm số đồng biến trên \(R\).

Câu 1: Xét sự đồng biến, nghịch biến của các hàm số:

a) \(y = 3{x^2} - 8{x^3}\)

b) \(y = 16x + 2{x^2} - {{16} \over 3}{x^3} - {x^4}\)

c) \(y = {x^3} - 6{x^2} + 9x\)

d) \(y = {x^4} + 8{x^2} + 5\)

Câu 2: Xét tính đơn điệu của các hàm số sau

a) \(y=\dfrac{\sqrt{x}}{x+100}\)

b) \(y=\dfrac{{{x}^{3}}}{\sqrt{{{x}^{2}}-6}}\)

Câu 3: Tìm các khoảng đồng biến, nghịch biến của các hàm số sau

a) \(y=\dfrac{3-2x}{x+7}\)

b) \(y=\dfrac{1}{(x-5)^2}\)

c) \(y=\dfrac{2x}{x^2-9}\)

Câu 4: Xác định tham số m để hàm số sau

a) \(y=\dfrac{mx-4}{x-m}\) đồng biến trên từng khoảng xác định

b) \(y=-x^3+mx^2-3x+4\) nghịch biến trên \((-\infty; +\infty)\)

Câu 5: Chứng minh phương trình sau có nghiệm duy nhất \(3(\cos x-1)+2\sin x+6x=0\).

Câu 1: Cho hàm số \(y = {x^2}(3 - x)\). Mệnh đề nào sau đây là đúng?

A. Hàm số đã cho đồng biến trên khoảng \(( - \infty ;0)\)

B. Hàm số đã cho đồng biến trên khoảng \((2; + \infty )\)

C. Hàm số đã cho đồng biến trên khoảng \(( - \infty ;3)\)

D. Hàm số đã cho đồng biến trên khoảng (0;2)

Câu 2: Cho hàm số \(y = \sqrt {{x^2} - 1} \). Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng \((0; + \infty )\)

B. Hàm số đồng biến trên \(( - \infty ; + \infty )\)

C.  Hàm số đồng biến trên khoảng \((1; + \infty )\)

D.  Hàm số nghịch biến trên khoảng \(( - \infty ;0)\)

Câu 3: Tìm tất cả các giá trị thực của tham số m để hàm số \(y = {x^3} - m{x^2} + 3x + 4\) đồng biến trên \(R\)

\(\begin{array}{l}
A.\;\; - 2 \le m \le 2\\
B.\;\; - 3 \le m \le 3\\
C.\;\;m \ge 3\\
D.\;\;m \le  - 3
\end{array}\)

Câu 4: Tìm tập hợp các giá trị của tham số thực m để hàm số \(y = \sqrt {{x^2} + 1}  - mx - 1\) đồng biến trên khoản \(\left( { - \infty ; + \infty } \right)\)

A. \(\left( { - \infty ;1} \right)\)

B. \(\left[ {1; + \infty } \right)\)

C. \(\left[ { - 1;1} \right]\)

D. \(\left( { - \infty ; - 1} \right]\)

Câu 5: Tìm tập hợp tất cả giá trị thực của tham số m sao cho hàm số \(y = \frac{{\left( {m + 1} \right)x + 2m + 2}}{{x + m}}\) nghịch biến trên khoảng \(\left( {-1; + \infty } \right)\)

A. \(m \in ( - \infty ;1) \cup (2; + \infty )\)

B. \(m \in \left[ {1; + \infty } \right)\)

C. \(m \in \left( { - 1;2} \right)\)

D. \(m \in \left[ {1;2} \right)\)

Qua bài học sẽ giúp các em nắm được

• Khái niệm thế nào là hàm số đồng biến, nghịch biến.
• Điều kiện để hàm số đơn điệu trên một miền.
• Các quy tắc xét tính đơn điệu của hàm số.