Giải bài tập SGK Toán 9 Bài 1: Hình trụ - Diện tích xung quanh và thể tích hình trụ

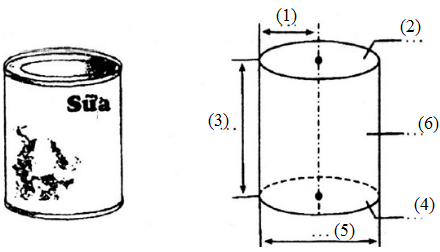
Hãy điền thêm các tên gọi vào dấu "..."

Phương pháp giải

Khi quay hình chữ nhật ABCD một vòng quanh cạnh CD cố định ta thu được một hình trụ.

- Hai đáy là hình tròn bằng nhau và nằm trên hai mặt phẳng song song.

- DC là trục của hình trụ.

- Các đường sinh của hình trụ ( chẳng hạn EF) vuông góc với hai mặt đáy.

Độ dài đường sinh cũng là độ dài đường cao của hình trụ.

Hướng dẫn giải

Đánh số các vị trí:

(1) Bán kính đường tròn đáy.

(2) Mặt đáy.

(3) Chiều cao.

(4) Mặt đáy.

(5) Đường kính đường tròn đáy.

(6) Mặt xung quanh.

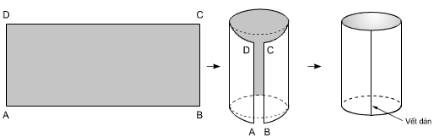
Lấy một băng giấy hình chữ nhật ABCD (h.80). Biết AB = 10cm, BC = 4cm; dán băng giấy như hình vẽ (B sát với A và C sát với D, không được xoắn).

Có thể dán băng giấy để tạo nên mặt xung quanh của hình trụ được không?

Phương pháp giải

Sử dụng giấy để làm thí nghiệm thực tế.

Khai triển mặt xung quanh của một hình trụ là một hình chữ nhật có chiều dài là chu vi đáy trụ và chiều rộng bằng chiều cao hình trụ. 

Hướng dẫn giải

Có thể dán băng giấy để tạo nên mặt xung quanh của hình trụ. Khi làm theo hướng dẫn ta được một hình trụ còn thiếu hai mặt đáy hình tròn.

Chiều cao của hình trụ là BC = 4cm.

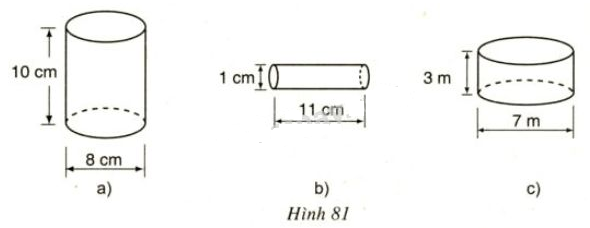
Quan sát ba hình dưới đây và chỉ ra chiều cao, bán kính của mỗi hình.

Phương pháp giải

Khi quay hình chữ nhật ABCD một vòng quanh cạnh CD cố định ta thu được một hình trụ.

- Hai đáy là hình tròn bằng nhau và nằm trên hai mặt phẳng song song.

- DC là trục của hình trụ.

- Các đường sinh của hình trụ ( chẳng hạn EF) vuông góc với hai mặt đáy.

Độ dài đường sinh cũng là độ dài đường cao của hình trụ.

Hướng dẫn giải

Gọi h là chiều cao, r là bán kính đáy của hình trụ.

Ta có:

Hình a: h = 10cm  và r =8:2= 4cm.

Hình b: h = 11cm và r = 1:2=0,5cm.

Hình c: h = 3m và  r  =7:2= 3,5m.

Một hình trụ có đáy là 7 cm, diện tích xung quanh bằng \(352 cm^2\). Khi đó, chiều cao của hình trụ là:

(A) 3,2 cm;                    (B) 4,6 cm;                     (C) 1,8 cm;

(D) 2,1 cm;                    (E) Một kết quả khác.

Phương pháp giải

Áp dụng công thức: \(S_{xq}=2\pi rh\)

trong đó: r là bán kính đáy, h là chiều cao

Hướng dẫn giải

Chiều cao của hình trụ là:

\(S_{xq}:(2\pi r)=352 : (14 \pi)\approx 8,01cm\)

Chọn (E)

Điền đầy đủ kết quả vào những ô trống của bảng sau:

Phương pháp giải

Cho hình trụ với bán kính đáy r và chiều cao h, ta có:

- Chu vi đáy: \(C=2\pi r\)

- Diện tích đáy: \(S=\pi r^2\)

- Diện tích xung quanh: \(S_{xq}=C.h=2\pi r h\)

- Thể tích: \(V=S.h=\pi r^2h\)

Hướng dẫn giải

+ Khi r = 1cm; h = 10cm thì hình trụ có

- Chu vi đáy \(C = 2\pi r = 2\pi \left( {cm} \right)\)

- Diện tích đáy là \(S = \pi {r^2} = \pi {.1^2} = \pi \left( {c{m^2}} \right)\)

- Diện tích xung quanh là \({S_{xq}} = 2\pi rh = 2\pi .1.10 = 20\pi \left( {c{m^2}} \right)\)

- Thể tích là \(V = \pi {r^2}h = \pi {.1^2}.10 = 10\pi \left( {c{m^3}} \right)\)

+ Khi r = 5cm; h = 4cm thì hình trụ có 

- Chu vi đáy \(C = 2\pi r = 2\pi .5 = 10\pi \left( {cm} \right)\)

- Diện tích đáy là \(S = \pi {r^2} = \pi {.5^2} = 25\pi \left( {c{m^2}} \right)\)

- Diện tích xung quanh là \({S_{xq}} = 2\pi rh = 2\pi .5.4 = 40\pi \left( {c{m^2}} \right)\)

- Thể tích là \(V = \pi {r^2}h = \pi {.5^2}.4 = 100\pi \left( {c{m^3}} \right)\)

+ Khi h = 8cm và chi vi đáy \(C = 4\pi\) thì hình trụ có

- Bán kính đáy \(r = \dfrac{C}{{2\pi }} = \dfrac{{4\pi }}{{2\pi }} = 2\left( {cm} \right)\)

- Diện tích đáy là \(S = \pi {r^2} = \pi {.2^2} = 4\pi \left( {c{m^2}} \right)\)

- Diện tích xung quanh là \({S_{xq}} = 2\pi rh = 2\pi .2.8 = 32\pi \left( {c{m^2}} \right)\)

- Thể tích là \(V = \pi {r^2}h = \pi {.2^2}.8 = 32\pi \left( {c{m^3}} \right)\)

Vậy ta có bảng sau:

Chiều cao của một hình trụ bằng bán kính đường tròn đáy. Diện tích xung quanh của hình trụ \(314 cm^2\).

Hãy tính bán kính đường tròn đáy và thể tích hình trụ (làm tròn kết quả đến chữ số thập phân thứ hai).

Phương pháp giải

Áp dụng công thức: \(S_{xq}=2\pi rh\)

trong đó: r là bán kính đáy, h là chiều cao

Hướng dẫn giải

Vì chiều cao hình trụ bằng bán kính đường tròn đáy nên \(h=r\)

Ta có:

\(S_{xq}=2\pi r h=2\pi r^2=314\\ \Rightarrow r^2\approx50\\ \Rightarrow r\approx 7,07cm\)

Thể tích của hình trụ là: \(V=\pi r^2h=\pi.50.\sqrt{50}\approx 1110,16 (cm^3)\)

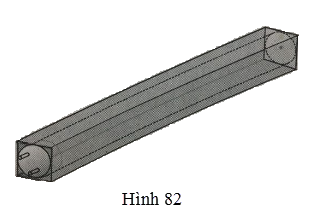
Một bóng đèn huỳnh quang dài 1,2m, đường kính của đường tròn đáy là 4cm, được đặt khít vào một ống giấy cứng dạng hình hộp (h.82). Tính diện tích phần giấy cứng dùng để làm một hộp.

Phương pháp giải

Diện tích phần giấy cứng dùng để làm hộp là diện tích xung quanh của một hình hộp chữ nhật có đáy là hình vuông ngoại tiếp đường tròn đường kính 4cm và chiều dài bằng chiều dài bóng đén.

Hướng dẫn giải

Chiều dài ống hình hộp là \(1,2m = 120cm\)

Chu vi đáy hình hộp là: \(4.4=16\,cm\)

Diện tích giấy cần dùng là: \(S=16.120=1920cm^2=0,192m^2\)