Giải bài tập SGK Toán 10 Chương 2 Bài 3: Phương trình đường Elip
Phần hướng dẫn giải bài tập Bài Phương trình đường Elip sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Hình học 10. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.
Mục lục nội dung

1. Giải bài 1 trang 88 SGK Hình học 10
Xác định độ dài các trục, tọa độ tiêu điểm, tọa độ các đỉnh và vẽ các elip có phương trình sau:
a) \(\frac{x^{2}}{25} + \frac{y^{2}}{9}= 1.\)
b) \(4x^2+ 9y^2= 1.\)
c) \(4x^2+ 9y^2= 36.\)
Phương pháp giải
Cho phương trình ellip: \(\left( E \right):\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{b^2} = 1.\)
Khi đó:
- Độ dài trục lớn là: \(2a\) và độ dài trục nhỏ là \(2b.\)
- Tọa độ các đỉnh là: \({A_1}\left( { - a;\;0} \right),\;{A_2}\left( {a;\;0} \right),\;{B_1}\left( { - b;\;0} \right),\)\(\;{B_2}\left( {b;\;0} \right).\)
- Tọa độ tiêu điểm: \({F_1}\left( { - c;\;0} \right),\;{F_2}\left( {c;\;0} \right)\) với \(c^2=a^2-b^2.\)
Hướng dẫn giải
Câu a:
Ta có: \(a^2= 25 \Rightarrow a = 5\) độ dài trục lớn \(2a = 10\)
\( b^2= 9 \Rightarrow b = 3\) độ dài trục nhỏ \(2a = 6\)
\(c^2= a^2– b^2= 25 - 9 = 16 \Rightarrow c = 4\)
Vậy hai tiêu điểm là : \(F_1(-4 ; 0)\) và \(F_2(4 ; 0)\)
Tọa độ các đỉnh \(A_1(-5; 0), A_2(5; 0), B_1(0; -3), B_2(0; 3)\).
Câu b:
\(4x^2+ 9y^2= 1\Leftrightarrow \dfrac{x^{2}}{\dfrac{1}{4}} + \dfrac{y^{2}}{\dfrac{1}{9}} = 1\)
\(a^2 =\dfrac{1}{4}\Rightarrow a = \dfrac{1}{2}\) \(\Rightarrow\) độ dài trục lớn \(2a = 1\)
\(b^2= \dfrac{1}{9}\Rightarrow b = \dfrac{1}{3}\) \(\Rightarrow\) độ dài trục nhỏ \(2b = \dfrac{2}{3}\)
\(c^2= a^2– b^2= \dfrac{1}{4}- \dfrac{1}{9} = \dfrac{5}{36}\) \(\Rightarrow c = \dfrac{\sqrt{5}}{6}\)
\(F_1(-\dfrac{\sqrt{5}}{6} ; 0)\) và \(F_2(\dfrac{\sqrt{5}}{6} ; 0)\)
\(A_1(-\dfrac{1}{2}; 0), A_2(\dfrac{1}{2}; 0)\), \(B_1(0; -\dfrac{1}{3} ), B_2(0; \dfrac{1}{3} )\).
Câu c:
Chia \(2\) vế của phương trình cho \(36\) ta được :
\(\dfrac{x^{2}}{9}+ \dfrac{y^{2}}{4}= 1\)
Ta có:
\(\begin{array}{l}
{a^2} = 9 \Rightarrow a = 3\\
{b^2} = 4 \Rightarrow b = 2\\
{c^2} = {a^2} - {b^2} = 5 \Rightarrow c = \sqrt 5
\end{array}\)
- Độ dài trục lớn \(2a = 6\)
- Độ dài trục nhỏ \( 2b = 4\).
- Tiêu điểm \(F_1(-\sqrt5 ; 0)\) và \(F_2(\sqrt5 ; 0)\)
- Các đỉnh \(A_1(-3; 0), A_2(3; 0), B_1(0; -2), B_2(0; 2)\).
2. Giải bài 2 trang 88 SGK Hình học 10
Lập phương trình chính tắc của elip, biết:
a) Trục lớn và trục nhỏ lần lượt là \(8\) và \(6.\)
b) Trục lớn bằng \(10\) và tiêu cự bằng \(6.\)
Phương pháp giải
- Độ dài trục lớn bằng \(2m \Rightarrow a=m.\)
- Độ dài trục nhỏ bằng \(2n \Rightarrow b=n.\)
- Tiêu cự bằng \(2t \Rightarrow c=t.\)
- \(c^2=a^2-b^2.\)
- Phương trình chính tắc của elip có dạng: \(\dfrac{x^{2}}{a^{2}} + \dfrac{y^{2}}{b^{2}} = 1.\)
Hướng dẫn giải
Câu a:
Phương trình chính tắc của elip có dạng : \(\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}} = 1.\)
Ta có \(a > b\):
\(2a = 8 \Rightarrow a = 4 \Rightarrow a^2= 16\)
\(2b = 6 \Rightarrow b = 3 \Rightarrow b^2= 9\)
Vậy phương trình chính tắc của elip có dạng \(\dfrac{x^{2}}{16}\) + \(\dfrac{y^{2}}{9}= 1\)
Câu b:
Ta có: \(2a = 10 \Rightarrow a = 5 \Rightarrow a^2= 25\)
\(2c = 6 \Rightarrow c = 3 \Rightarrow c^2= 9\)
\(\Rightarrow b^2=a^2-c^2 \Rightarrow b^2= 25 - 9 = 16\)
Vậy phương trình chính tắc của elip có dạng \(\dfrac{x^{2}}{25} + \dfrac{y^{2}}{16}= 1\)
3. Giải bài 3 trang 88 SGK Hình học 10
Lập phương trình chính tắc của elip trong các trường hợp sau:
a) Elip đi qua các điểm \(M(0; 3)\) và \(N( 3; \dfrac{-12}{5}).\)
b) Một tiêu điểm là \(F_1( -\sqrt3; 0)\) và điểm \(M(1; \dfrac{\sqrt{3}}{2})\) nằm trên elip.
Phương pháp giải
Câu a:
Phương trình chính tắc của elip có dạng: \(\dfrac{x^{2}}{a^{2}} + \dfrac{y^{2}}{b^{2}} = 1\)
Thay tọa độ các điểm M, N thuộc ellip vào phương trình ellip để tìm a và b
Câu b:
Phương trình chính tắc của elip có dạng: \(\dfrac{x^{2}}{a^{2}} + \dfrac{y^{2}}{b^{2}} = 1\)
- Từ tiêu điểm F ta suy ra được c.
- Sử dụng công thức \(c^2=a^2-b^2.\)
Hướng dẫn giải
Câu a:
Phương trình chính tắc của elip có dạng: \(\dfrac{x^{2}}{a^{2}} + \dfrac{y^{2}}{b^{2}} = 1\)
Elip đi qua \(M(0; 3)\)
\(\dfrac{0^{2}}{a^{2}} + \dfrac{3^{2}}{b^{2}}= 1 \) \(\Leftrightarrow \dfrac{9}{{{b^2}}} = 1 \) \(\Rightarrow b^2= 9\)
Elip đi qua \(N( 3; \dfrac{-12}{5})\)
\(\dfrac{3^{2}}{a^{2}} + \dfrac{\left(\dfrac{-12}{5}\right)^{2}}{9} = 1\) \( \Leftrightarrow \dfrac{9}{{{a^2}}} = \dfrac{9}{{25}}\) \( \Rightarrow a^2= 25\)
Phương trình chính tắc của elip là : \(\dfrac{x^{2}}{25} + \dfrac{y^{2}}{9} = 1\)
Câu b:
Ta có: \({F_1}\left( { - \sqrt 3 ;0} \right) \Rightarrow - c = - \sqrt 3 \) \( \Leftrightarrow c = \sqrt 3 \) \( \Rightarrow c^2= 3\)
Elip đi qua điểm \(M(1; \dfrac{\sqrt{3}}{2})\)
\(\dfrac{1}{a^{2}} + \dfrac{\left(\dfrac{\sqrt{3}}{2}\right)^{2}}{b^{2}}= 1 \) \( \Rightarrow \dfrac{1}{a^{2}}+ \dfrac{3}{4b^{2}}= 1\) (1)
Mặt khác: \( c^2=a^2-b^2\)
\(\Rightarrow 3 = a^2-b^2\Rightarrow a^2=b^2 + 3\)
Thế vào (1) ta được : \(\dfrac{1}{b^{2}+ 3} + \dfrac{3}{4b^{2}} = 1\)
\(\begin{array}{l}
\Leftrightarrow \dfrac{{4{b^2} + 3{b^2} + 9}}{{4{b^4} + 12{b^2}}} = 1\\
\Leftrightarrow 4{b^2} + 3{b^2} + 9 = 4{b^4} + 12{b^2}\\
\Leftrightarrow 4{b^4} + 5{b^2} - 9 = 0\\
\Leftrightarrow \left[ \begin{array}{l}
{b^2} = 1\left( {TM} \right)\\
{b^2} = - \dfrac{9}{4}\left( {loai} \right)
\end{array} \right.\\
\Rightarrow {a^2} = {b^2} + 3 = 1 + 3 = 4
\end{array}\)
Phương trình chính tắc của elip là : \(\dfrac{x^{2}}{4} + \dfrac{y^{2}}{1}= 1\)
4. Giải bài 4 trang 88 SGK Hình học 10
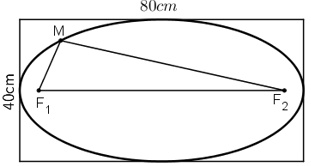
Để cắt một bảng hiệu quảng cáo hình elip có các trục lớn là \(80cm\) và trục nhỏ là \(40 cm\) từ một tấm ván ép hình chữ nhật có kích thước \(80cm \times 40cm\), người ta vẽ một hình elip lên tấm ván như hình 3.19. Hỏi phải ghim hai cái đinh cách các mép tấm ván ép bao nhiêu và lấy vòng dây có độ dài là bao nhiêu?
Phương pháp giải
+) Chu vi vòng dây là: \(F_1 F_2+2a.\)
Hướng dẫn giải
Ta có: \(2a = 80 \Rightarrow a = 40\)
\(2b = 40\Rightarrow b = 20\)
\( c^2= a^2– b^2= 1200 \Rightarrow c = 20\sqrt 3\)
Phải đóng đinh tại các điểm \(F_1, F_2\).
Khi đó khoảng cách từ hai chiếc đinh \(F_1,F_2\) đến mép ván là:
\(F_2A_2=F_1A_1 = OA_2 – OF_2\) \(=a-c= 40 - 20\sqrt3\)
\(\Rightarrow F_2A_2 = 20(2 - \sqrt3) ≈ 5,4cm\)
Chu vi vòng dây bằng: \(F_1F_2+ MF_1+MF_2 \) \(= 2c+2a = 40\sqrt 3 + 80\)
\( = 40(2 + \sqrt 3)\)\( ≈ 149,3cm\)
5. Giải bài 5 trang 88 SGK Hình học 10
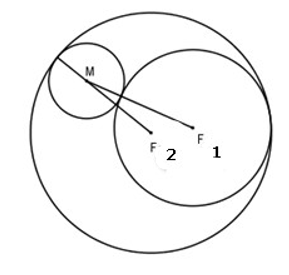
Cho hai đường tròn \({C_1}({F_1};{R_1})\) và \({C_2}({F_2};{R_2})\). \(C_1\) nằm trong \(C_2\) và \(F_1≠ F_2\). Đường tròn \((C)\) thay đổi luôn tiếp xúc ngoài với \(C_1\) và tiếp xúc trong với \(C_2\).Hãy chứng tỏ rằng tâm \(M\) của đường tròn \((C)\) di động trên một elip.
Phương pháp giải
- Tính \(MF_1,MF_2\) theo các bán kính, chú ý điều kiện tiếp xúc ngoài, tiếp xúc trong.
- Tính \(MF_1+MF_2\) và sử dụng định nghĩa elip để suy ra đpcm.
Hướng dẫn giải
Gọi \(R\) là bán kính của đường tròn \((C)\)
\((C)\) và \(C_1\) tiếp xúc ngoài với nhau
\( \Rightarrow \)\(MF_1= R_1+ R\) (1)
\((C)\) và \(C_2\) tiếp xúc trong với nhau
\( \Rightarrow \)\(MF_2= R_2- R\) (2)
Từ (1) và (2) ta được
\(M{F_1} + M{F_2} = {R_1}+R + {R_2}-R\) \(=R_1+R_2\) không đổi.
Điểm M có tổng các khoảng cách \(M{F_1} + M{F_2} \) đến hai điểm cố định \(F_1\) và \(F_2\) bằng một độ dài không đổi \({R_1} + {R_2}.\)
Vậy tập hợp điểm \(M\) là đường elip, có các tiêu điểm \(F_1\) và \(F_2\) và có tiêu cự \(F_1F_2= R_1+R_2.\)
Tham khảo thêm
- doc Giải bài tập SGK Toán 10 Chương 2 Bài 1: Phương trình đường thẳng
- doc Giải bài tập SGK Toán 10 Chương 2 Bài 2: Phương trình đường tròn
- doc Giải bài tập SGK Toán 10 Ôn tập chương 3: Phương pháp tọa độ trong mặt phẳng