Giải bài tập SGK Toán 11 Chương 4 Bài 3: Hàm số liên tục

Dùng định nghĩa xét tính liên tục của hàm số \(f(x) = x^3 + 2x - 1\) tại \(x_0 = 3\)

Phương pháp giải

Hàm số \(y=f(x)\) có tập xác định \(D\) liên tục tại \({x_0 \in D}\)

\( \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).

Hướng dẫn giải

Hàm số \(f(x) = x^3+ 2x - 1\) xác định trên \(\mathbb R\) và \(x_0= 3 ∈ \mathbb R\).

Ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to 3} f\left( x \right) = {3^3} + 2.3 - 1 = 32\\f\left( 3 \right) = {3^3} + 2.3 - 1 = 32\end{array} \right. \) \(\Rightarrow \mathop {\lim }\limits_{x \to 3} f\left( x \right) = f\left( 3 \right)\).

Vậy hàm số đã cho liên tục tại điểm \(x_0= 3\).

a) Xét tính liên tục của hàm số \(y = g(x)\) tại \(x_0 = 2\), biết 

 \(g(x) =\left\{\begin{matrix} \frac{x^{3}-8}{x- 2}&nếu&x\neq 2 \\ 5&nếu& x=2 \end{matrix}\right.\)

b) Trong biểu thức xác định g(x) ở trên, cần thay số 5 bởi số nào để hàm số liên tục tại \(x_0 = 2\)

Phương pháp giải

Hàm số \(y=f(x)\) có tập xác định \(D\) liên tục tại \({x_0 \in D}\)

\( \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).

Hướng dẫn giải

a) Ta có:

\(\begin{array}{l}
\mathop {\lim }\limits_{x \to 2} g\left( x \right) = \mathop {\lim }\limits_{x \to 2} \dfrac{{{x^3} - 8}}{{x - 2}}\\= \mathop {\lim }\limits_{x \to 2} \dfrac{{(x-2)(x^2+2x+4)}}{{x - 2}}\\ = \mathop {\lim }\limits_{x \to 2} \left( {{x^2} + 2x + 4} \right)\\
= {2^2} + 2.2. + 4 = 12\\
g\left( 2 \right) = 5\\
\Rightarrow \mathop {\lim }\limits_{x \to 2} g\left( x \right) \ne g\left( 2 \right)
\end{array}\)

Vì \(\underset{x\rightarrow 2}{\lim} g(x) ≠ g(2)\) nên hàm số \(y = g(x)\) gián đoạn tại \(x_0= 2\).

b) Để hàm số \(y = g(x)\) liên tục tại \(x_0= 2\) \( \Rightarrow \mathop {\lim }\limits_{x \to 2} g\left( x \right) = g\left( 2 \right) = 12 \Rightarrow \) ta cần thay số \(5\) bởi số \(12\).

Cho hàm số  \(f(x) =\left\{\begin{matrix} 3x + 2&nếu& x<-1\\ x^{2}-1 &nếu& x \geq -1 \end{matrix}\right.\)

a) Vẽ đồ thị của hàm số \(y = f(x)\). Từ đó nêu nhận xét về tính liên tục của hàm số trên tập xác định của nó.

b) Khẳng định nhận xét trên bằng một chứng minh.

Phương pháp giải

a) Khi \(x<-1\), vẽ đường thẳng \(y=3x+2\). Khi \(x \ge -1\), vẽ parabol \(y=x^2-1\).

b) Hàm số \(y=f(x)\) liên tục tại điểm \(x_0\) \(\Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)

Hướng dẫn giải

a) Vẽ đồ thị hàm số y=f(x).

Tập xác định của hàm số \(\mathbb{R}\)

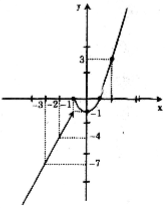
Đồ thị f(x) = 3x+2 (với x<-1) là phần đường thẳng qua các điểm (-2;-4)(-3;-7).

Đồ thị f(x) = x2 -1 (với \(x\geq -1\)) là parabol.

Đỉnh (0;-1)

Bề lõm hướng lên trên.

Cắt trục hoành tại (-1;0) và (1;0).

Căn cứ vào đồ thị ta thấy hàm số không liên tục tại điểm x= -1, liên tục trên các khoảng \((-\infty ;-1)\) và \((-1;+\infty )\).

b) Nếu \(x < -1\): \(f(x) = 3x + 2\) liên tục trên \((-∞; -1)\) (vì đây là hàm đa thức nên liên tục trên tập xác định của nó).

Nếu \(x> -1\): \(f(x) = x^2- 1\) liên tục trên \((-1; +∞)\) (vì đây là hàm đa thức nên liên tục trên tập xác định của nó).

Xét tính liên tục của hàm số tại \(x = -1\);

Ta có 

\(\underset{x\rightarrow -1^{-}}{\lim} f(x) = \)\(\underset{x\rightarrow -1^{-}}{\lim} (3x + 2) = 3(-1) +2 = -1\).

\(\underset{x\rightarrow -1^{+}}{\lim} f(x) = \underset{x\rightarrow -1^{+}}{\lim} (x^2- 1)\)\( = (-1)^2- 1 = 0\).

Vì \(\underset{x\rightarrow -1^{-}}{\lim} f(x) ≠ \underset{x\rightarrow -1^{+}}{\lim} f(x)\) nên không tồn tại \(\underset{x\rightarrow -1}{\lim} f(x)\).

Vậy hàm số gián đoạn tại \(x_0= -1\).

Cho hàm số  \(f(x) =\frac{x +1}{x^{2}+x-6}\) và \(g(x) = tanx + sin x\)

Với mỗi hàm số, hãy xác định các khoảng trên đó hàm số liên tục

Phương pháp giải

Hàm phân thức, hàm lượng giác liên tục trên các khoảng xác định của chúng.

Hướng dẫn giải

Hàm số \(f(x) = \dfrac{x +1}{x^{2}+x-6}\) xác định khi và chỉ khi:

\({x^2} + x - 6 \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne - 3\\x \ne 2\end{array} \right.\) \( \Rightarrow D = R\backslash \left\{ { - 3;2} \right\}\)

Hàm số \(f(x)\) là hàm phân thức nên liên tục trên các khoảng xác định.

Vậy f(x) liên tục trên các khoảng \((-∞; -3), (-3; 2)\) và \((2; +∞)\)

Hàm số \(g\left( x \right) = \tan x + \sin x\) xác định khi và chỉ khi 

\(\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi \,\,\left( {k \in Z} \right)\)

Hàm số \(g(x)\) là hàm lượng giác nên liên tục trên các khoảng xác định.

Vậy g(x) liên tục trên các khoảng \(( - \dfrac{\pi }{2}+kπ;  \dfrac{\pi }{2}+kπ)\) với \(k ∈ \mathbb Z\).

Ý kiến sau đúng hay sai?

"Nếu hàm số \(y = f(x)\) liên tục tại điểm \(x_0\) còn hàm số \(y = g(x)\) không liên tục tại x0, thì \(y = f(x) + g(x)\) là một hàm số không liên tục tại \(x_0\)." 

Phương pháp giải

Chứng minh phản chứng: giả sử ngược lại hàm số \(y = f(x) + g(x)\) là hàm số liên tục tại \(x_0\), chứng minh điều này là vô lý.

Hướng dẫn giải

Ý kiến trên đúng.

Giả sử ngược lại hàm số \(y = f(x) + g(x)\) liên tục tại \(x_0\).

Đặt \(h(x) = f(x) + g(x)\) liên tục tại \(x=x_0\).

\( \Rightarrow g(x) = h(x) - f(x)\).

Vì \(y = h(x)\) và \(y = f(x)\) liên tục tại \(x_0\) \( \Rightarrow h\left( x \right);\,\, - f\left( x \right)\) là các hàm số liên tục tại \(x_0\).

Theo giả sử ta có hàm số \(h\left( x \right) + \left( { - f\left( x \right)} \right) = h\left( x \right) - f\left( x \right) = g\left( x \right)\) phải liên tục tại \(x_0\). Điều này trái với giả thiết là \(y = g(x)\) không liên tục tại \(x_0\).

Vậy giả sử ban đầu sai. Chứng tỏ \(y = f(x) + g(x)\) không liên tục tại \(x_0\).

Chứng minh rằng phương trình:

a) \(2x^3 + 6x + 1 = 0\) có ít nhất hai nghiệm

b) \(cosx = x\) có nghiệm

Phương pháp giải

- Xét các hàm số vế trái của phương trình.

- Tìm hai điểm bất kì và tính tích các giá trị của hàm số tại hai điểm đó.

+ Nếu tích nhỏ hơn \(0\) thì ta kết luận phương trình có ít nhất một nghiệm trong khoảng hai giá trị ấy.

+ Nếu tích lớn hơn \(0\) thì ta không kết luận gì và tìm giá trị khác để tính.

Hướng dẫn giải

a) Xét hàm số \(f(x)=2x^3-6x + 1\) là hàm đa thức nên liên tục trên \(\mathbb R\).

Ta có:

\(f\left( 0 \right) = {2.0^3} - 6.0 + 1 = 1;\)

\(f\left( 1 \right) = {2.1^3} - 6.1 + 1 =  - 3;\)

\(f\left( { - 2} \right) = 2.{\left( { - 2} \right)^3} - 6.\left( { - 2} \right) + 1 =  - 3\)

+) \(f\left( 0 \right).f\left( 1 \right) = 1.\left( { - 3} \right) < 0\) nên phương trình có ít nhất 1 nghiệm \(x_0 \in (0; 1)\).

+) \(f\left( 0 \right).f\left( -2 \right) = 1.\left( { - 3} \right) < 0\) nên phương trình có ít nhất 1 nghiệm \(x_1 \in (-2; 0)\).

Mà \(\left( {0;1} \right) \cup \left( { - 2;0} \right) = \emptyset  \Rightarrow x_0 \ne x_1 \Rightarrow \) phương trình \(f(x) = 0\) có ít nhất hai nghiệm.

b) \(\cos x = x \Leftrightarrow \cos x - x = 0\)

Xét hàm số \(g\left( x \right) = \cos x - x\) xác định trên \(\mathbb R\) nên liên tục trên \(\mathbb R\).

Ta có:

\(g\left( 0 \right) = \cos 0 - 0 = 1 - 0 = 1;\)

\(g\left( {\dfrac{\pi }{2}} \right) = \cos \dfrac{\pi }{2} - \dfrac{\pi }{2} =  - \dfrac{\pi }{2}\)

\(g\left( 0 \right).g\left( {\dfrac{\pi }{2}} \right) = 1.\left( { - \dfrac{\pi }{2}} \right) =  - \dfrac{\pi }{2} < 0\) nên phương trình đã cho có ít nhất 1 nghiệm thuộc khoảng \((0; \dfrac{\pi }{2})\).