Giải bài tập SBT Toán 10 Bài 1: Hàm số
Mời các em học sinh lớp 10 cùng tham khảo nội dung giải bài tập SBT bài Hàm số trang 29 - 31 dưới đây. Bài gồm có 9 bài tập được eLib sưu tầm và tổng hợp. Với nội dung chi tiết, rõ ràng giúp các em ôn tập lại các kiến thức đã học và vận dụng vào giải các bài tập tương tự. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy của quý thầy cô và học tập của các em học sinh.
Mục lục nội dung
1. Giải bài 2.1 trang 29 SBT Đại số 10
2. Giải bài 2.2 trang 30 SBT Đại số 10
3. Giải bài 2.3 trang 30 SBT Đại số 10
4. Giải bài 2.4 trang 30 SBT Đại số 10
5. Giải bài 2.5 trang 31 SBT Đại số 10
6. Giải bài 2.6 trang 31 SBT Đại số 10
7. Giải bài 2.7 trang 31 SBT Đại số 10

1. Giải bài 2.1 trang 29 SBT Đại số 10
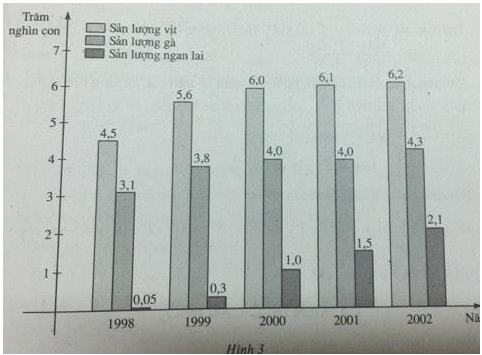
Biểu đồ sau (h.3) biểu thị sản lượng vịt, gà và ngan lai qua 5 năm của một trang trại. Coi y = f(x), y = g(x) và y = h(x) tương ứng là các hàm số biểu thị sự phụ thuộc số vịt, số gà và số ngan lai vào thời gian x. Qua biểu đồ, hãy:
a) Tìm tập xác định của mỗi hàm số đã nêu.
b) Tìm các giá trị f(2002), g(1999), h(2000) và nêu ý nghĩa của chúng;
c) Tìm hiệu h(2002) – h(1999) và nêu ý nghĩa của nó.
Phương pháp giải
Sử dụng các kiến thức về hàm số, tập xác định của hàm số:
Cho \(D \subset R, D ≠ \phi\). Một hàm số xác định trên D là một quy tắc f cho tương ứng mỗi số x ∈ D với một và duy nhất chỉ một số y ∈ R. Ta kí hiệu:
\(\begin{array}{l}f:D \to \mathbb{R}\\\,\,\,\,\,\,\,\,x \mapsto y = f\left( x \right)\end{array}\)
Tập hợp D được gọi là tập xác định (hay miền xác định), x được gọi là biến số, \(y_0= f(x_0)\) tại x = x0
Hướng dẫn giải
a) Tập xác định của cả ba hàm số y = f(x), y = g(x) và y = h(x) là:
D = {1998, 1999, 2000, 2001, 2002}
b) f(2002) = 620000 (con)
g(1999) = 380000 (con)
h(2000) = 100000 (con)
Năm 2002 sản lượng của trang trại là 620 000 con vịt ; năm 1999 sản lượng là 380 000 con gà ; năm 2000 trang trại có sản lượng là 100 000 con ngan lai.
c) h(2002) - h(1999) = 210000 - 30000 = 180000 (con)
Sản lượng ngan lai của trang trại năm 2002 tăng 180 000 con so với năm 1999.
2. Giải bài 2.2 trang 30 SBT Đại số 10
Tìm tập xác định của các hàm số
a) \(y = - {x^5} + 7x - 2\)
b) \(y = \dfrac{{3x + 2}}{{x - 4}}\)
c) \(y = \sqrt {4x + 1} - \sqrt { - 2x + 1}\)
d) \(y = \dfrac{{2x + 1}}{{(2x + 1)(x - 3)}}\)
Phương pháp giải
Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa. Như vậy để tìm được tập xác định thì chúng ta cần đi tìm điều kiện xác định của biểu thức f(x). Biểu thức f(x) thường gặp là một số dạng sau:
+ \(f(x)=\dfrac{A(x)}{B(x)}\) thì f(x) xác định khi và chỉ khi \(B(x)\neq 0\)
+ \(f(x)=\sqrt{P(x)}\) thì f(x) xác định khi và chỉ khi \(P(x)\geq 0\)
+ \(f(x)=\dfrac{A(x)}{\sqrt{B(x)}}\) thì f(x) xác định khi và chỉ khi B(x)> 0
+ \(f(x)=\dfrac{\sqrt{A(x)}}{\sqrt{B(x)}}\) thì f(x) xác định khi và chỉ khi \(A(x)\geq 0\) và \(B(x)> 0\)
Hướng dẫn giải
a) y\là một đa thức nên tập xác định của hàm số đã cho là \(D = \mathbb{R}\)
b) \(y\) là một phân thức nên mẫu thức \(x - 4 \ne 0\) hay \(x \ne 4\)
Vậy tập xác định của hàm số đã cho là \(D = \mathbb{R}\backslash \left\{ 4 \right\}\)
c) Hàm số xác định với các giá trị của x thỏa mãn
\(\left\{ {\begin{array}{*{20}{c}}{4x + 1 \ge 0}\\{ - 2x + 1 \ge 0}\end{array}} \right. hay \left\{ {\begin{array}{*{20}{c}}{x \ge \dfrac{{ - 1}}{4}}\\{x \le \dfrac{1}{2}}\end{array}} \right. \Leftrightarrow \dfrac{{ - 1}}{4} \le x \le \dfrac{1}{2}\)
Vậy tập xác định của hàm số đã cho là \(D = \left[ { - \dfrac{1}{4};\dfrac{1}{2}} \right]\)
d) y là một phân thức nên mẫu thức \(\left( {2x + 1} \right)\left( {x - 3} \right) \ne 0 \,\, hay \,\, x \ne \dfrac{{ - 1}}{2} \,\,và\,\, x \ne 3\)
Vậy tập xác định của hàm số đã cho là \(D = \mathbb{R}\backslash \left\{ {\dfrac{{ - 1}}{2};3} \right\}\)
3. Giải bài 2.3 trang 30 SBT Đại số 10
Cho hàm số
\(y = f(x) = \left\{ \begin{array}{l}\dfrac{{2x - 3}}{{x - 1}}{\rm{ }}\text { với }x \le 0\\ - {x^2} + 2x{\rm{ }} \text { với }x > 0\end{array} \right.\)
Tính giá trị của hàm số đó tại x = 5; x = - 2; x = 0; x = 2
Phương pháp giải
Kiểm tra với mỗi giá trị của x thì x thuộc khoảng nào và \(f\left( x \right)\) bằng gì sau đó thay giá trị của x vào biểu thức đó rồi tính
Hướng dẫn giải
Với x = 5 > 0 ta có: \(f(5) = - {5^2} + 2.5 = - 25 + 10 = - 15\)
Với x = - 2 < 0 ta có: \(f( - 2) = \dfrac{{2.( - 2) - 3}}{{ - 2 - 1}} = \dfrac{7}{3}\)
Với x = 0 ta có: \(f(0) = \dfrac{{2.0 - 3}}{{0 - 1}} = 3\)
Với x = 2 > 0 ta có: \(f(2) = {\left( { - 2} \right)^2} + 2.2 = 0\)
4. Giải bài 2.4 trang 30 SBT Đại số 10
Cho các hàm số \(f(x) = {x^2} + 2 + \sqrt {2 - x} ;\)
\(g(x) = - 2{x^3} - 3x + 5\)
\(u(x) = \left\{ \begin{array}{l}\sqrt {3 - x} ,x < 2\\\sqrt {{x^2} - 4} ,x \ge 2\end{array} \right.\); \(v(x) = \left\{ \begin{array}{l}\sqrt {6 - x} ,x \le 0\\{x^2} + 1,x > 0\end{array} \right.\)
Tính các giá trị \(f( - 2) - f(1);g(3);f( - 7) - g( - 7);\)
\(f( - 1) - u( - 1);u(3) - v(3);\)
\(v(0) - g(0);\dfrac{{f(2) - f( - 2)}}{{v(2) - v( - 3)}}\)
Phương pháp giải
Kiểm tra với mỗi giá trị của x thì x thuộc khoảng nào và \(u\left( x \right),v\left( x \right)\) bằng biểu thức nào sau đó thay giá trị của x vào biểu thức đó rồi tính
Hướng dẫn giải
Ta có: \(f(x) = {x^2} + 2 + \sqrt {2 - x};\)
\(g(x) = - 2{x^3} - 3x + 5\)
\(u(x) = \left\{ \begin{array}{l}\sqrt {3 - x} ,x < 2\\\sqrt {{x^2} - 4} ,x \ge 2\end{array} \right.\); \(v(x) = \left\{ \begin{array}{l}\sqrt {6 - x} ,x \le 0\\{x^2} + 1,x > 0\end{array} \right.\)
Suy ra
\(f( - 2) - f(1) = {( - 2)^2} + 2 + \sqrt {2 + 2} \)
\(- ({1^2} + 2 + \sqrt {2 - 1} ) = 8 - 4 = 4\)
\(g(3) = - {2.3^3} - 3.3 + 5 = - 58\)
\(f( - 7) - g( - 7) = {( - 7)^2} + 2 + \sqrt {2 + 7} - {\rm{[}} - 2.{( - 7)^3} - 3.( - 7) + 5] = - 658\)
\(f( - 1) - u( - 1) = {\left( { - 1} \right)^2} + 2 + \sqrt {2 - \left( { - 1} \right)} - \sqrt {3 - \left( { - 1} \right)} \)
\(= 3 + \sqrt 3 - 2 = 1 + \sqrt 3 \)
Do \(- 1 < 2 \Rightarrow u\left( { - 1} \right) = \sqrt {3 - \left( { - 1} \right)} \)
\(u(3) - v(3) = \sqrt {{3^2} - 4} - ({3^2} + 1)\)
\(= \sqrt 5 - 10\); (do 3 > 2 > 0)
\(v(0) - g(0) = \sqrt {6 - 0}\)
\(-\left( { - 2.0 - 3.0 + 5} \right) = \sqrt 6 - 5\)
\(\dfrac{{f(2) - f( - 2)}}{{v(2) - v( - 3)}} = \dfrac{{6 - 8}}{{5 - 3}} = - 1\)
5. Giải bài 2.5 trang 31 SBT Đại số 10
Xét tính đồng biến, nghịch biến của hàm số trên các khoảng tương ứng
a) y = - 2x + 3 trên R.
b) \(y = {x^2} + 10x + 9\) trên \(( - 5; + \infty )\)
c) \(y = - \dfrac{1}{{x + 1}}\) trên ( - 3; - 2) và (2 ;3).
Phương pháp giải
\(\forall {x_1},{x_2} \in \mathbb{R}\), giả sử \({x_1} > {x_2}\,\, ta\,\, xét \,\,xem \,\,f({x_1}) < f({x_2}) \,\, hay \,\, f({x_1}) > f({x_2})\) rồi đưa ra kết luận nghịch biến hay đồng biến dựa vào định nghĩa.
Hướng dẫn giải
a) \(\forall {x_1},{x_2} \in \mathbb{R}\) ta có:
\(f({x_1}) - f({x_2})\)
\(= - 2{x_1} + 3 - ( - 2{x_2} + 3) \)
\(= - 2({x_1} - {x_2})\)
Ta thấy \({x_1} > {x_2}\) thì \(-2({x_1} - {x_2}) < 0,\) tức là
\(f({x_1}) - f({x_2}) < 0 \Leftrightarrow f({x_1}) < f({x_2})\)
Vậy hàm số đã cho nghịch biến trên R
b) \(\forall {x_1},{x_2} \in \mathbb{R}\), ta có:
\(f({x_1}) - f({x_2}) = x_1^2 + 10{x_1} + 9 - x_2^2 - 10{x_2} - 9\)
= \(({x_1} - {x_2})({x_1} + {x_2}) + 10({x_1} - {x_2})\)
= \(({x_1} - {x_2})({x_1} + {x_2} + 10)\)(*)
\(\forall {x_1},{x_2} \in ( - 5; + \infty ) và {x_1} < {x_2}\) ta có
\({x_1} - {x_2} < 0 \,\,và\,\, {x_1} + {x_2} + 10 > 0\) vì
\({x_1} > - 5;{x_2} > - 5 = > {x_1} + {x_2} > - 10\)
Vậy từ (*) suy ra
\(f({x_1}) - f({x_2}) < 0 \Leftrightarrow f({x_1}) < f({x_2})\)
Hàm số đồng biến trên khoảng \(( - 5; + \infty )\)
c) \(\forall {x_1},{x_2} \in ( - 3; - 2) \,\, và \,\, {x_1} < {x_2}\), ta có:
\({x_1} - {x_2} < 0;{x_1} + 1 < - 2 + 1 < 0;\)
\({x_2} + 1 < - 2 + 1 < 0 = >\)
\(({x_1} + 1)({x_2} + 1) > 0\). Vậy
\(f({x_1}) - f({x_2}) = - \dfrac{1}{{{x_1} + 1}} + \dfrac{1}{{{x_2} + 1}}\)
\(= \dfrac{{{x_1} - {x_2}}}{{({x_1} + 1)({x_2} + 1)}} < 0\)
\(\Leftrightarrow f({x_1}) < f({x_2})\)
Do đó hàm số đồng biến trên khoảng ( - 3; - 2)
\(\forall {x_1},{x_2} \in (2;3)\) và \({x_1} < {x_2}\), tương tự ta cũng có \(f({x_1}) < f({x_2})\)
Vậy hàm số đồng biến trên khoảng (2;3).
6. Giải bài 2.6 trang 31 SBT Đại số 10
Xét tính chẵn, lẻ của các hàm số
a) y = - 2
b) \(y = 3{x^2} - 1\)
c) \(y = - {x^4} + 3x - 2\)
d) \(y = \dfrac{{ - {x^4} + {x^2} + 1}}{x}\)
Phương pháp giải
Ta xét với mỗi \(x \in D\) thì - x có thuộc D hay không và f( - x) = f(x) hay f( - x) = - f(x) hay \(f( - x) \ne f(x) \ne f\left( { - x} \right)\) rồi đưa ra kết luận dựa vào định nghĩa hàm số chẵn, hàm số lẻ.
Hướng dẫn giải
a) Tập xác định \(D = \mathbb{R}\) và \(\forall x \in D\) có \(- x \in D \,\,và \,\, f( - x) = - 2 = f(x)\)
Hàm số là hàm số chẵn.
b) Tập xác định \(D = \mathbb{R}\); \(\forall x \in D\) có \(- x \in D\) và \(f( - x) = 3.{( - x)^2} - 1 = 3{x^2} - 1 = f(x)\)
Vậy hàm số đã cho là hàm số chẵn.
c) Tập xác định \(D = \mathbb{R}\), nhưng \(f(1) = - 1 + 3 - 2 = 0\) còn \(f( - 1) = - 1 - 3 - 2 = - 6\) nên \(f( - 1) \ne f(1)\) và \(f( - 1) \ne - f(1)\)
Vậy hàm số đã cho không là hàm số chẵn cũng không là hàm số lẻ.
d) Tập xác định \(D = \mathbb{R}\backslash \left\{ 0 \right\}\) nên nếu \(x \ne 0 \,\, và \,\,x \in D\) thì \(- x \in D\). Ngoài ra,
\(f( - x) = \dfrac{{ - {{( - x)}^4} + {{( - x)}^2} + 1}}{{ - x}} \)\(= \dfrac{{ - {x^4} + {x^2} + 1}}{{ - x}} = -\dfrac{{ - {x^4} + {x^2} + 1}}{x} \)\(= - f(x)\)
Vậy hàm số đã cho là hàm số lẻ.
7. Giải bài 2.7 trang 31 SBT Đại số 10
Tập xác định của hàm số \(y = \dfrac{{3x + 10}}{{{x^2} + 14x + 45}}\) là
A. \(\mathbb{R}\)
B. \(\mathbb{R}\backslash \left\{ { - 5;9} \right\}\)
C. \(\mathbb{R}\backslash \left\{ { - 5; - 9} \right\}\)
D. \(\mathbb{R}\backslash \left\{ {5;9} \right\}\)
Phương pháp giải
Áp dụng cách tìm điều kiện xác định của hàm số đã học từ
Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa. Như vậy để tìm được tập xác định thì chúng ta cần đi tìm điều kiện xác định của biểu thức f(x). Biểu thức f(x) thường gặp là một số dạng sau:
+ \(f(x)=\dfrac{A(x)}{B(x)}\) thì f(x) xác định khi và chỉ khi \(B(x)\neq 0\)
+ \(f(x)=\sqrt{P(x)}\) thì f(x) xác định khi và chỉ khi \(P(x)\geq 0\)
+ \(f(x)=\dfrac{A(x)}{\sqrt{B(x)}}\) thì f(x) xác định khi và chỉ khi B(x)> 0
+ \(f(x)=\dfrac{\sqrt{A(x)}}{\sqrt{B(x)}}\) thì f(x) xác định khi và chỉ khi \(A(x)\geq 0\) và \(B(x)> 0\)
Hướng dẫn giải
\(y = \dfrac{{3x + 10}}{{{x^2} + 14x + 45}}\) là một phân thức
nên mẫu thức \({x^2} + 14x + 45 \ne 0\) hay
\(x \ne - 5\) và \(x \ne - 9\)
Vậy tập xác định của hàm số đã cho là
\(D = \mathbb{R}\backslash \left\{ { - 5; - 9} \right\}\)
Đáp án đúng C
8. Giải bài 2.8 trang 31 SBT Đại số 10
Hàm số \(y = \sqrt {x + 7} + \dfrac{2}{{{x^2} + 6x - 16}}\) có tập xác định D bằng
A. \(\left( {7; + \infty } \right)\)
B. \(\left( {7; + \infty } \right)\backslash \left\{ { - 8;2} \right\}\)
C. \(\left[ { - 7;7} \right]\backslash \left\{ 2 \right\}\)
D. \(\left[ { - 7; + \infty } \right)\backslash \left\{ 2 \right\}\)
Phương pháp giải
Áp dụng cách tìm điều kiện xác định của hàm số đã học từ
Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa. Như vậy để tìm được tập xác định thì chúng ta cần đi tìm điều kiện xác định của biểu thức f(x). Biểu thức f(x) thường gặp là một số dạng sau:
+ \(f(x)=\dfrac{A(x)}{B(x)}\) thì f(x) xác định khi và chỉ khi \(B(x)\neq 0\)
+ \(f(x)=\sqrt{P(x)}\) thì f(x) xác định khi và chỉ khi \(P(x)\geq 0\)
+ \(f(x)=\dfrac{A(x)}{\sqrt{B(x)}}\) thì f(x) xác định khi và chỉ khi B(x)> 0
+ \(f(x)=\dfrac{\sqrt{A(x)}}{\sqrt{B(x)}}\) thì f(x) xác định khi và chỉ khi \(A(x)\geq 0\) và \(B(x)> 0\)
Hướng dẫn giải
Hàm số xác định với các giá trị của x thỏa mãn
\(\left\{ {\begin{array}{*{20}{c}}{x + 7 \ge 0}\\{{x^2} + 6x - 16 \ne 0}\end{array}} \right.\) hay
\(\left\{ {\begin{array}{*{20}{c}}{x \ge - 7}\\{x \ne - 8{\rm\text{ và }}x \ne 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ge - 7}\\{x \ne 2}\end{array}} \right.\)
Vậy tập xác định của hàm số đã cho là
\(D = \left[ { - 7; + \infty } \right)\backslash \left\{ 2 \right\}\)
Chọn đáp án D
9. Giải bài 2.9 trang 31 SBT Đại số 10
Cho các hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{{x^2} - 1\text{ với }x \le 3}\\{\sqrt {x + 2}\text{ với }x > 3}\end{array}} \right.;\)\(g\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{2x + 3\text{ với }x > 1}\\{{x^2} + 2\text{ với }x \le 1}\end{array}} \right.\)
Khi đó giá trị: \(f\left( 0 \right) + 2f\left( 7 \right) - g\left( 1 \right)\) bằng:
A. 2 B. 0
C. \(\sqrt 2 + 3\) D.- 2
Phương pháp giải
Kiểm tra với mỗi giá trị của x thì x thuộc khoảng nào và \(f\left( x \right),g\left( x \right)\) bằng biểu thức nào sau đó thay giá trị của x vào biểu thức đó rồi tính
Hướng dẫn giải
Do 0 < 3 nên \(f\left( 0 \right) = {0^2} - 1 = - 1\)
Do 7 > 3 nên \(f\left( 7 \right) = \sqrt {7 + 2} = 3\)
Do 1 = 1 nên \(g\left( 1 \right) = {1^2} + 2 = 3\)
Suy ra \(f\left( 0 \right) + 2f\left( 7 \right) - g\left( 1 \right) = - 1 + 2.3 - 3 \) = 2
Chọn đáp án A
Các em hãy luyện tập bài trắc nghiệm Hàm số Toán 10 sau để nắm rõ thêm kiến thức bài học.
Tham khảo thêm
- doc Giải bài tập SBT Toán 10 Bài 2: Hàm số y = ax + b
- doc Giải bài tập SBT Toán 10 Bài 3: Hàm số bậc hai



